Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

4. zadaća (zadatak)
WWW:
Idite na Prethodno  1, 2, 3  Sljedeće
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Linearna algebra 1 & 2 (za inženjerske smjerove)
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Atomised
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Sarma = la pohva - posuda
70 = 95 - 25
Lokacija: Exotica
PostPostano: 13:59 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
[quote="punio4"]
Ma dobro, ali što mi je ~cilj~ dobiti?
[/quote]

Jednostavniji oblik iz kojeg lako vidiš koja su rješenja...

Ma sve ti je isto kao i da rješavaš sustav jednadžbi bez matrica... Samo ti je ovako lakše jer ne moraš pisati sve one ikseve. Možeš ti u bilo kojem trenutku ponovo zapisati ono što si dobio (da je ekvivalentno početnoj matrici) u obliku sustava jednadžbi, ali obično se to radi tek na kraju, kad skroz pojednostaviš matricu.

Jedina možda razlika je u tome što smo kod sustava bez matrica obično svodili na trokutasti oblik, a ovdje poništavamo i elemente iznad (ne samo one ispod)... Ali ta razlika nije nužna, čisto je praktične prirode.
punio4 (napisa):

Ma dobro, ali što mi je ~cilj~ dobiti?


Jednostavniji oblik iz kojeg lako vidiš koja su rješenja...

Ma sve ti je isto kao i da rješavaš sustav jednadžbi bez matrica... Samo ti je ovako lakše jer ne moraš pisati sve one ikseve. Možeš ti u bilo kojem trenutku ponovo zapisati ono što si dobio (da je ekvivalentno početnoj matrici) u obliku sustava jednadžbi, ali obično se to radi tek na kraju, kad skroz pojednostaviš matricu.

Jedina možda razlika je u tome što smo kod sustava bez matrica obično svodili na trokutasti oblik, a ovdje poništavamo i elemente iznad (ne samo one ispod)... Ali ta razlika nije nužna, čisto je praktične prirode.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Gost
PostPostano: 14:03 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
O zadatku s r(AB):
Hint. Jedan način - matrica se može napisati kao umnožak elementarnih matrica i kanonske matrice, do oblika npr. A = S K T, pri čemu su S i T regularne, kao umnožak elementarnih, a K kanonska. Množenje elementarnim matricama ne mijenja rang. Množenje s kanonskom može sačuvati ili smanjiti rang (provjeriti, ako nije očito).
O zadatku s r(AB):
Hint. Jedan način - matrica se može napisati kao umnožak elementarnih matrica i kanonske matrice, do oblika npr. A = S K T, pri čemu su S i T regularne, kao umnožak elementarnih, a K kanonska. Množenje elementarnim matricama ne mijenja rang. Množenje s kanonskom može sačuvati ili smanjiti rang (provjeriti, ako nije očito).


[Vrh]
Atomised
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Sarma = la pohva - posuda
70 = 95 - 25
Lokacija: Exotica
PostPostano: 14:12 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
[quote="Anonymous"]O zadatku s r(AB):
Hint. Jedan način - matrica se može napisati kao umnožak elementarnih matrica i kanonske matrice, do oblika npr. A = S K T, pri čemu su S i T regularne, kao umnožak elementarnih, a K kanonska. Množenje elementarnim matricama ne mijenja rang. Množenje s kanonskom može sačuvati ili smanjiti rang (provjeriti, ako nije očito).[/quote]

Hvala. :)
Anonymous (napisa):
O zadatku s r(AB):
Hint. Jedan način - matrica se može napisati kao umnožak elementarnih matrica i kanonske matrice, do oblika npr. A = S K T, pri čemu su S i T regularne, kao umnožak elementarnih, a K kanonska. Množenje elementarnim matricama ne mijenja rang. Množenje s kanonskom može sačuvati ili smanjiti rang (provjeriti, ako nije očito).


Hvala. Smile


[Vrh]
Korisnički profil Pošaljite privatnu poruku
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 14:56 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
Ok. Reducirao sam ovo što se više može i dobio:
[latex]\begin{bmatrix}
1&1&1&-1&7&|&2\\
1&-1,&6&0&1&|&4\\
2&1&1&1&0&|&6\end{bmatrix}
\sim
\begin{bmatrix}
1&0&0&2&7&|&4\\
0&1&0&-4&-18&|&-12/5\\
0&0&1&1&4&|&2/5\end{bmatrix}[/latex]
Kako sad ovo zapisati kao parametarsko rješenje?
Ok. Reducirao sam ovo što se više može i dobio:

Kako sad ovo zapisati kao parametarsko rješenje?




Zadnja promjena: punio4; 15:20 sri, 13. 2. 2008; ukupno mijenjano 2 put/a.
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Atomised
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Sarma = la pohva - posuda
70 = 95 - 25
Lokacija: Exotica
PostPostano: 15:04 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
[quote="punio4"]
Kako sad ovo zapisati kao parametarsko rješenje?[/quote]

Gledaš ove stupce u kojima imaš više ne-nula i nepoznanice iz tih stupaca su jednake parametrima. Doduše, ne moraš uzeti baš te stupce za parametarske ali tako je najjednostavnije.
punio4 (napisa):

Kako sad ovo zapisati kao parametarsko rješenje?


Gledaš ove stupce u kojima imaš više ne-nula i nepoznanice iz tih stupaca su jednake parametrima. Doduše, ne moraš uzeti baš te stupce za parametarske ali tako je najjednostavnije.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 15:32 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
Jasno, hvala puno :D
Jasno, hvala puno Very Happy


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
vancika
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Sarma = la pohva - posuda
3 = 6 - 3
Lokacija: Varaždin
PostPostano: 16:41 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
jel neko u 5. zadatku dobio slucajeve kad je lam=2,!=2,!=19 i tak... ??
jel neko u 5. zadatku dobio slucajeve kad je lam=2,!=2,!=19 i tak... ??



_________________
People are strange when you're a stranger...
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Atomised
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Sarma = la pohva - posuda
70 = 95 - 25
Lokacija: Exotica
PostPostano: 16:44 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
[quote="vancika"]jel neko u 5. zadatku dobio slucajeve kad je lam=2,!=2,!=19 i tak... ??[/quote]

Ja sam dobio za 1 i -19...

Sad, je li mi točno, ne znam. ;)
vancika (napisa):
jel neko u 5. zadatku dobio slucajeve kad je lam=2,!=2,!=19 i tak... ??


Ja sam dobio za 1 i -19...

Sad, je li mi točno, ne znam. Wink


[Vrh]
Korisnički profil Pošaljite privatnu poruku
vancika
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Sarma = la pohva - posuda
3 = 6 - 3
Lokacija: Varaždin
PostPostano: 16:51 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
ja sam za 2 i 19... daj provjeri jos jemput i ak nades gresku javi jer se meni neda :D e i imam pitanje... dok trazimo rang onda mozemo delati transformacije i po redcima i po stupcima,kod inverza ili jedno ili drugo a kod determinante isto tak?? ili ne? i samo kod determinante ide = a kod ostalog onaj tilda...
ja sam za 2 i 19... daj provjeri jos jemput i ak nades gresku javi jer se meni neda Very Happy e i imam pitanje... dok trazimo rang onda mozemo delati transformacije i po redcima i po stupcima,kod inverza ili jedno ili drugo a kod determinante isto tak?? ili ne? i samo kod determinante ide = a kod ostalog onaj tilda...



_________________
People are strange when you're a stranger...
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Atomised
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Sarma = la pohva - posuda
70 = 95 - 25
Lokacija: Exotica
PostPostano: 16:58 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
[quote="vancika"]ja sam za 2 i 19... daj provjeri jos jemput i ak nades gresku javi jer se meni neda :D [/quote]

[url=http://wims.unice.fr/wims/en_tool~linear~linsolver.en.html]Onaj linear solver[/url] daje rezultate u skladu s mojim rješenjem. :) Ako nisam nešto krivo shvatio, naravno...
vancika (napisa):
ja sam za 2 i 19... daj provjeri jos jemput i ak nades gresku javi jer se meni neda Very Happy


Onaj linear solver daje rezultate u skladu s mojim rješenjem. Smile Ako nisam nešto krivo shvatio, naravno...


[Vrh]
Korisnički profil Pošaljite privatnu poruku
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 18:05 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
Božesačuvaj koje izraze dobivam s desne strane kad je lambda != 1...
Idem opet... Dobivam neke 21-nine. Mathematica veli da bi u nazivniku trebalo biti a + 19...
Ha idemo opet...
Božesačuvaj koje izraze dobivam s desne strane kad je lambda != 1...
Idem opet... Dobivam neke 21-nine. Mathematica veli da bi u nazivniku trebalo biti a + 19...
Ha idemo opet...


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 18:26 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
Mogu reducirat matricu do:
[latex]\begin{bmatrix}
1&1&1&-1&|&1\\
1&2&2&1&|&2\\
0&3&-1&7&|&-1\\
1&1&\lambda &4&|&2
\end{bmatrix}
\sim
\begin{bmatrix}
1&0&0&-3&|&0\\
0&1&9&0&|&9\\
0&0&\lambda + 19&0&|&21\\
0&0&-4&1&|&-4
\end{bmatrix}
[/latex]

Jel još kome tako ispalo?
[EDIT]
Opet krivo zbrojio dio -_-
Ja ću sutra sa svim riješenim uspit skupit 3 boda ako ovako nastavim...
Mogu reducirat matricu do:


Jel još kome tako ispalo?
[EDIT]
Opet krivo zbrojio dio -_-
Ja ću sutra sa svim riješenim uspit skupit 3 boda ako ovako nastavim...


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Gost
PostPostano: 20:28 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
punio4 meni ispalo ko i tebi..
punio4 meni ispalo ko i tebi..


[Vrh]
BitterSweet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: žensko
Sarma = la pohva - posuda
27 = 45 - 18
Lokacija: sjeverno od raja
PostPostano: 20:35 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
evo moj 4. kako je ispao:
t(-3,3,-1,1,0)+z(-7,18,-4,0,1)+(4,-12/5,2/5,0,0)

jeli to točno, i ako je jel treba što sređivat ili je gotovo?
evo moj 4. kako je ispao:
t(-3,3,-1,1,0)+z(-7,18,-4,0,1)+(4,-12/5,2/5,0,0)

jeli to točno, i ako je jel treba što sređivat ili je gotovo?


[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
.bubamara.
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 03. 10. 2007. (17:32:18)
Postovi: (4E)16
Spol: žensko
Sarma = la pohva - posuda
13 = 14 - 1
PostPostano: 20:44 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
[quote="BitterSweet"]evo moj 4. kako je ispao:
t(-3,3,-1,1,0)+z(-7,18,-4,0,1)+(4,-12/5,2/5,0,0)

jeli to točno, i ako je jel treba što sređivat ili je gotovo?[/quote]

ev i meni su zadnja dva ovak ispala, ali prvi mi je (-2,4,-1,1,0)
BitterSweet (napisa):
evo moj 4. kako je ispao:
t(-3,3,-1,1,0)+z(-7,18,-4,0,1)+(4,-12/5,2/5,0,0)

jeli to točno, i ako je jel treba što sređivat ili je gotovo?


ev i meni su zadnja dva ovak ispala, ali prvi mi je (-2,4,-1,1,0)



_________________
Uživam na snijegu
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
BitterSweet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: žensko
Sarma = la pohva - posuda
27 = 45 - 18
Lokacija: sjeverno od raja
PostPostano: 20:49 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
super, mislim da si u pravu, jer sam ja prvi put za t-parametar pogriješila u predznaku pa sam ovo na brzinu ispravljala...
ali ako to ispravim i pretpostavimo da je točno, jeli to rješenje ili treba još sređivat nešto
super, mislim da si u pravu, jer sam ja prvi put za t-parametar pogriješila u predznaku pa sam ovo na brzinu ispravljala...
ali ako to ispravim i pretpostavimo da je točno, jeli to rješenje ili treba još sređivat nešto


[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
.bubamara.
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 03. 10. 2007. (17:32:18)
Postovi: (4E)16
Spol: žensko
Sarma = la pohva - posuda
13 = 14 - 1
PostPostano: 20:53 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
pa onak kak smo i na vježbama radili:
ispišeš rješenje X kao stupac i onda ga rastaviš kao zbroj parametarskog rješenja (rješenja pripadnog homogenog sustava) i rješenja originalnog sustava (ovaj zadnji vektor)

i to je to ;)
pa onak kak smo i na vježbama radili:
ispišeš rješenje X kao stupac i onda ga rastaviš kao zbroj parametarskog rješenja (rješenja pripadnog homogenog sustava) i rješenja originalnog sustava (ovaj zadnji vektor)

i to je to Wink



_________________
Uživam na snijegu
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
punio4
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: muško
Sarma = la pohva - posuda
3 = 11 - 8
Lokacija: Zagreb
PostPostano: 20:55 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
[latex](x_1,x_2,x_3,x_4,x_5)=t(-2,4,-1,1,0)+s(-7,18,-4,0,1)+(4,-\frac{12}{5},\frac{2}{5},0,0); \ t, \ s\in\mathbb{R}[/latex]
Ovo je točno rješenje.
Inače, može li mi netko pomoći [url=http://degiorgi.math.hr/forum/viewtopic.php?t=10803]kako se rješavaju LU matrice?[/url]

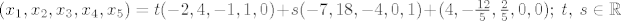
Ovo je točno rješenje.
Inače, može li mi netko pomoći kako se rješavaju LU matrice?


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
BitterSweet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: žensko
Sarma = la pohva - posuda
27 = 45 - 18
Lokacija: sjeverno od raja
PostPostano: 20:57 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
super, hvala...
mi nismo skupa na vježbama, a što smo mi radili, he he.
ma bolje ne govorit ništa
super, hvala...
mi nismo skupa na vježbama, a što smo mi radili, he he.
ma bolje ne govorit ništa


[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
ekatarina
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: žensko
Sarma = la pohva - posuda
30 = 47 - 17
PostPostano: 21:33 sri, 13. 2. 2008    Naslov: Citirajte i odgovorite
[quote="Atomised"][quote="vancika"]ja sam za 2 i 19... daj provjeri jos jemput i ak nades gresku javi jer se meni neda :D [/quote]

[url=http://wims.unice.fr/wims/en_tool~linear~linsolver.en.html]Onaj linear solver[/url] daje rezultate u skladu s mojim rješenjem. :) Ako nisam nešto krivo shvatio, naravno...[/quote]

ja sam samo za -19, ne znam zašto treba i za taj 1, on je dolje u posljednjem retku (lambda - 1) i onda se odmah u slijedećoj matrci to izgubi.
Atomised (napisa):
vancika (napisa):
ja sam za 2 i 19... daj provjeri jos jemput i ak nades gresku javi jer se meni neda Very Happy


Onaj linear solver daje rezultate u skladu s mojim rješenjem. Smile Ako nisam nešto krivo shvatio, naravno...


ja sam samo za -19, ne znam zašto treba i za taj 1, on je dolje u posljednjem retku (lambda - 1) i onda se odmah u slijedećoj matrci to izgubi.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Linearna algebra 1 & 2 (za inženjerske smjerove) Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2, 3  Sljedeće
Stranica 2 / 3.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan