| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
nameless
Forumaš(ica)


Pridružen/a: 29. 09. 2007. (13:59:36)
Postovi: (58)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
nameless
Forumaš(ica)


Pridružen/a: 29. 09. 2007. (13:59:36)
Postovi: (58)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
felixx
Forumaš(ica)

Pridružen/a: 27. 11. 2007. (15:31:43)
Postovi: (61)16
Lokacija: *obrisano*
|
 Postano: 16:01 čet, 14. 2. 2008 Naslov: Postano: 16:01 čet, 14. 2. 2008 Naslov: |
    |
|
|
ok, uspio sam ga rijesiti kad sam isao doma (dok sam se zivcirao jer mi je pauk digao auto).... nda...
dakle, evo rjesenja...
kljucno se sjetiti definicije determinante preko permutacija...
rjesenje ima dva dijela
1. dio ako je n neparan
pp. da ste odabrali neki a u svoju permutaciju
kad njega izlucite (2 broja b vise ne smijete koristiti), a uz svaki od tih b se u retku/stupcu nalazi a kao jedini broj iz tok retka/stupcu koji uopce mozete iskoristit za permutaciju koja nema 0, zanimljivo je za primjetiti da ce ti novi 'a' koje treba iskoristit bit ili za (+2,+2) ili za (-2,-2) od pocetnog po koordinatama modulo n, dakle 2 reda iznad ili dva reda ispod... e sad posto je n neparan znate da cete se tek nakon n ovakvih koraka vratiti u pocetnu polje, tj. imate potpunu permutaciju koja je oblika +- a^n
e sad kako ste vi odabrali sve brojeve na glavnoj dijagonali, u toj permutaciji nema inverzija pa je Ep = 1
dakle u det imate + a^n
sad pretpostavite da ste odabrali neki b
analogno kao u pret. slucaju, taj b ce ponistiti za permutaciju 2 broja a, te ce u njihovom retku/stupcu ostati po jedan b kao jedini broj koji mozete iskoristiti za permutaciju(a vi znate da iz svakog retka/stupca morate uzeti bar jedan), i udaljenost tih novih b ce bit kao u prethodnom slucaju po koodinatama (+2,+2) ili (-2,-2) od pocetnog...
opet kako je n neparan nakon n ovakvih koraka cete se vratiti u pocetno polje i imat cete punu permutaciju...
sad preostaje odrediti inverziju te nase permutacije
ako pogledate raspored ovih b, prva dva su iza svih ostalih dakle
2 * (n-2) inverzija sto je parno pa je Ep = 1
dakle imamo + b^n u det
ovime smo pokazali da nijedna druga permutacija nece dati broj razl. od 0, jer ako uzmemo jedan a moramo uzeti i preostalih n-1, analagono i za b
dakle ako je n neparan
det A = a^n + b^n
e sad
ako je n paran
imamo slican postupak samo treba primjetiti da cemo se ovdje nakon
n/2 koraka vratiti u pocetnu tocku, dakle ako uzmemo jedan a, uzet cemo jos i njih n/2 - 1
analogno i za b
a to jos nije potpuna permutacija
dakle pp. da smo uzeli neki a
onda moramo uzeti jos i n/2- 1 a
sad smo iskoristili svaki drugi stupac i svaki drugi redak... i sad mozemo za preostalih n-1 uzeti samo b-ove ili samo a-ove
analogno ako ej prvi b
dobijemo da postoje samo 4 permutacije koje daju umnozak razl. od 0
a to su a^n, - (ab)^n/2, - (ab)^n/2, + b^n,
ovaj kraj sam malo ubrzao, ali lako se moze skuziti zasto vrijedi....
dakle det A = a^n - (ab)^n/2 - (ab)^n/2 + b^n
ok, uspio sam ga rijesiti kad sam isao doma (dok sam se zivcirao jer mi je pauk digao auto).... nda...
dakle, evo rjesenja...
kljucno se sjetiti definicije determinante preko permutacija...
rjesenje ima dva dijela
1. dio ako je n neparan
pp. da ste odabrali neki a u svoju permutaciju
kad njega izlucite (2 broja b vise ne smijete koristiti), a uz svaki od tih b se u retku/stupcu nalazi a kao jedini broj iz tok retka/stupcu koji uopce mozete iskoristit za permutaciju koja nema 0, zanimljivo je za primjetiti da ce ti novi 'a' koje treba iskoristit bit ili za (+2,+2) ili za (-2,-2) od pocetnog po koordinatama modulo n, dakle 2 reda iznad ili dva reda ispod... e sad posto je n neparan znate da cete se tek nakon n ovakvih koraka vratiti u pocetnu polje, tj. imate potpunu permutaciju koja je oblika +- a^n
e sad kako ste vi odabrali sve brojeve na glavnoj dijagonali, u toj permutaciji nema inverzija pa je Ep = 1
dakle u det imate + a^n
sad pretpostavite da ste odabrali neki b
analogno kao u pret. slucaju, taj b ce ponistiti za permutaciju 2 broja a, te ce u njihovom retku/stupcu ostati po jedan b kao jedini broj koji mozete iskoristiti za permutaciju(a vi znate da iz svakog retka/stupca morate uzeti bar jedan), i udaljenost tih novih b ce bit kao u prethodnom slucaju po koodinatama (+2,+2) ili (-2,-2) od pocetnog...
opet kako je n neparan nakon n ovakvih koraka cete se vratiti u pocetno polje i imat cete punu permutaciju...
sad preostaje odrediti inverziju te nase permutacije
ako pogledate raspored ovih b, prva dva su iza svih ostalih dakle
2 * (n-2) inverzija sto je parno pa je Ep = 1
dakle imamo + b^n u det
ovime smo pokazali da nijedna druga permutacija nece dati broj razl. od 0, jer ako uzmemo jedan a moramo uzeti i preostalih n-1, analagono i za b
dakle ako je n neparan
det A = a^n + b^n
e sad
ako je n paran
imamo slican postupak samo treba primjetiti da cemo se ovdje nakon
n/2 koraka vratiti u pocetnu tocku, dakle ako uzmemo jedan a, uzet cemo jos i njih n/2 - 1
analogno i za b
a to jos nije potpuna permutacija
dakle pp. da smo uzeli neki a
onda moramo uzeti jos i n/2- 1 a
sad smo iskoristili svaki drugi stupac i svaki drugi redak... i sad mozemo za preostalih n-1 uzeti samo b-ove ili samo a-ove
analogno ako ej prvi b
dobijemo da postoje samo 4 permutacije koje daju umnozak razl. od 0
a to su a^n, - (ab)^n/2, - (ab)^n/2, + b^n,
ovaj kraj sam malo ubrzao, ali lako se moze skuziti zasto vrijedi....
dakle det A = a^n - (ab)^n/2 - (ab)^n/2 + b^n
_________________
bla bla
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 17:14 čet, 14. 2. 2008 Naslov: Postano: 17:14 čet, 14. 2. 2008 Naslov: |
    |
|
|
Kakav sam ja imao:
[latex]\begin{vmatrix}
b & 0&\cdots&0 & a \\
0 & 0 & \cdots &a & b \\
\vdots&\cdots&a&b&0\\
0&a&b&\cdots&\vdots\\
a&b & \cdots & 0&0
\end{vmatrix}[/latex]
Uglavnom. Ja sam išao na laplaceov razvoj po prvom retku, jer imam samo a i b, ostalo su mi 0.
Dakle imam [latex]-b\cdot\begin{vmatrix}
0&\cdots&a&b\\
\vdots&a&b&\vdots\\
a&b&\cdots&0\end{vmatrix}+(-1)^n a\cdot\begin{vmatrix}
0&\cdots&a&b\\
\vdots&a&b&\vdots\\
a&b&\cdots&0\end{vmatrix}[/latex]
Sad tu moram raditi (n-1)/2 zamjena redaka i stupaca, ovisno da li je n paran ili neparan, da dobijem nule ispod dijagonale i a na dijagonali.
[latex]-b\cdot(-1)^{\lfloor\frac{n-1}{2}\rfloor}a^{n-1}+(-1)^n a^{n-1}\cdot(-1)^{\lfloor\frac{n-1}{2}\rfloor}[/latex]
[EDIT]
Zeznul sam u ispitu, a i tu... Prva matrica ispadaju b na dijagonali, a druga a na dijagonali... pa je onda prvi b^n, a ne i on a^n.
Dobro rješenje je (mislim):
[latex]-b\cdot(-1)^{\lfloor\frac{n-1}{2}\rfloor}b^{n-1}+(-1)^n a^{n-1}\cdot(-1)^{\lfloor\frac{n-1}{2}\rfloor}[/latex]
[EDIT2]
Aaaaarg! :wall:
Stavio sam i n, umjesto n-1. Zaboravio sam da je stupanj manje...
[URL=http://i4.photobucket.com/albums/y136/Punio4/120294430056.png][img]http://i4.photobucket.com/albums/y136/Punio4/th_120294430056.png[/img][/URL]
Kakav sam ja imao:

Uglavnom. Ja sam išao na laplaceov razvoj po prvom retku, jer imam samo a i b, ostalo su mi 0.
Dakle imam 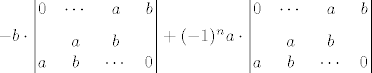
Sad tu moram raditi (n-1)/2 zamjena redaka i stupaca, ovisno da li je n paran ili neparan, da dobijem nule ispod dijagonale i a na dijagonali.
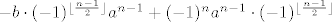
[EDIT]
Zeznul sam u ispitu, a i tu... Prva matrica ispadaju b na dijagonali, a druga a na dijagonali... pa je onda prvi b^n, a ne i on a^n.
Dobro rješenje je (mislim):
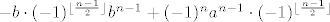
[EDIT2]
Aaaaarg! 
Stavio sam i n, umjesto n-1. Zaboravio sam da je stupanj manje...

|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
 Postano: 21:33 čet, 14. 2. 2008 Naslov: Postano: 21:33 čet, 14. 2. 2008 Naslov: |
    |
|
|
[quote="Novi"]Mislim da bi trebalo za parni n biti det A = a^n - (-ab)^n/2 - (-ab)^n/2 + b^n. (putem dugotrajnog raspisivanja)[/quote]
Mislim da si u pravu (za n=6 sam provjerio na primjeru a=1, b=2 na http://www.math.odu.edu/~bogacki/cgi-bin/lat.cgi?c=det ), felixx ionako nije objašnjavao računanje broja inverzija za parne n, ali to se lako ispravi...
Izgleda da se može riješiti poništavanjem onih beova ispod dijagonale..
ja sam se naspavao ali i dalje ne mogu baš mislit :D dobro, budem sutra mislio. :D
punio, vaša je puno puno lakša...
Jel se sjećaš možda vašeg sustava?
| Novi (napisa): | | Mislim da bi trebalo za parni n biti det A = a^n - (-ab)^n/2 - (-ab)^n/2 + b^n. (putem dugotrajnog raspisivanja) |
Mislim da si u pravu (za n=6 sam provjerio na primjeru a=1, b=2 na http://www.math.odu.edu/~bogacki/cgi-bin/lat.cgi?c=det ), felixx ionako nije objašnjavao računanje broja inverzija za parne n, ali to se lako ispravi...
Izgleda da se može riješiti poništavanjem onih beova ispod dijagonale..
ja sam se naspavao ali i dalje ne mogu baš mislit  dobro, budem sutra mislio. dobro, budem sutra mislio. 
punio, vaša je puno puno lakša...
Jel se sjećaš možda vašeg sustava?
_________________
Nikola Adžaga
Građevinski fakultet, Sveučilište u Zagrebu
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:53 čet, 14. 2. 2008 Naslov: Postano: 21:53 čet, 14. 2. 2008 Naslov: |
    |
|
|
Ono s lambdama?
Da. Bilo ih je sveskup 3 u matrici, od čega 1 u skupu rješenja.
Dok sam sveo lijevih 4x3 na kanonski oblik, u zadnjem stupcu i rješenjima su se nakotile lambde da je to bio užas. Njih 8.
Većina je bila oblika lamda-1, 2lambda-2, ali je bilo i par koji su odstupali od toga...
Riješio sam za lambda = 0 (nema rješenja), i lambda = 1 (jedinstveno), a dalje nisam imao POJMA što da radim s tim čudom.
Valjda sam fulao negdje.
Ono s lambdama?
Da. Bilo ih je sveskup 3 u matrici, od čega 1 u skupu rješenja.
Dok sam sveo lijevih 4x3 na kanonski oblik, u zadnjem stupcu i rješenjima su se nakotile lambde da je to bio užas. Njih 8.
Većina je bila oblika lamda-1, 2lambda-2, ali je bilo i par koji su odstupali od toga...
Riješio sam za lambda = 0 (nema rješenja), i lambda = 1 (jedinstveno), a dalje nisam imao POJMA što da radim s tim čudom.
Valjda sam fulao negdje.
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
guscerica
Forumaš(ica)
Pridružen/a: 15. 02. 2008. (15:21:08)
Postovi: (9)16
Spol: 
|
 Postano: 15:33 pet, 15. 2. 2008 Naslov: Postano: 15:33 pet, 15. 2. 2008 Naslov: |
    |
|
|
malo kasnim...al ono sta felixx napisa...nista ja to ne razumijem,pogubila sam se usred objasnjenja(svejedno hvala na komentaru,moze bit da je netko shvatio :lol: )...
uglavnom dobih isti rezultat ako je n paran i ako je n neparan, al nikakve permutacije ja ne uzimah u obzir...
drzah se samo laplaceovog razvoja i pomalo...(jesam ispisala jako puno,al uspila sam dobit to...)
sad ili sam stvarno zaribala, pa mi se nekako posrecilo da sam dobila rezultat, nekin cudom...ili sam uspjela rijesiti "pjeske"...hm...sve mi se cini da je ovo prvo :oops:
malo kasnim...al ono sta felixx napisa...nista ja to ne razumijem,pogubila sam se usred objasnjenja(svejedno hvala na komentaru,moze bit da je netko shvatio  )... )...
uglavnom dobih isti rezultat ako je n paran i ako je n neparan, al nikakve permutacije ja ne uzimah u obzir...
drzah se samo laplaceovog razvoja i pomalo...(jesam ispisala jako puno,al uspila sam dobit to...)
sad ili sam stvarno zaribala, pa mi se nekako posrecilo da sam dobila rezultat, nekin cudom...ili sam uspjela rijesiti "pjeske"...hm...sve mi se cini da je ovo prvo 
|
|
| [Vrh] |
|
|













