| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
buzov5
Forumaš(ica)

Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
 Postano: 17:03 sub, 16. 2. 2008 Naslov: Postano: 17:03 sub, 16. 2. 2008 Naslov: |
    |
|
|
2. mislim da da, al taj dio teorije tek moram sam sebi dokazat :)
4. je, gledas ko kompoziciju i to samo dvije funkcije..i(x)=e^x g:R->R i h(x)=||f(x)||^2 h:R^n->R. sad je g(x)=i(h(x)) a obje ove su difenercijabilne pa je Dg(x)=Di(h(x))Dh(x). lako se vidi da je Di(x)=e^x i Dh(x)=2x (ovo drugo se moze dokazat preko parcijalnih derivacija dosta lako ak ne vidis iz prve jer je h(x)=x_1^2+x_2^2+...+x_n^2) pa bi konacno rjesenje bilo
Dg(x)=e^(||f(x)||^2)*2f(x) (nadam se da nijesam fulao nigdje)
5. ovo je fora. teorem srednje vrijednosti kaze da za bilo koje tocke(vektore) x i y postoji tocka E na segmetnu x,y( naravno ako je fja definirana na cijelom segmentu, a ovdje ocito je) tako da je f(x)-f(y)=D(E)(x-y) a znas da je D(E)=A jer je to zadano u zadatku pa onda imas da za bilo koje x i y vrijedi f(x)-f(y)=Ax-Ay => f(x)-Ax=f(y)-Ay za bilo koje x i y iz R^n p taj izraz mora biti konstanta(i taj izraz je neki vektor iz R^m) pa to oznacimo s b i sad dobivas f(x)-Ax=b tj f(x)=Ax+b... ah, ovo je lijep zadatak :)
6.gledaj fju korijen(x)..ako onda u tocki x_0 postize maksimum onda i funkcija f(x)=x postize u toj tockli maksimum jer ako postize u nekoj drugoj tocki y onda bi imao y=f(y)>=f(x)=x ali iz prve funkcije i maksimalnosti imas korijen(x)>=korijen(y) pa kad to kvadriras imas x>=y iz cega ide x=y.ista stvar za minimum.. eto tolko..treba sad ucit dalje za usmeni ;)
2. mislim da da, al taj dio teorije tek moram sam sebi dokazat 
4. je, gledas ko kompoziciju i to samo dvije funkcije..i(x)=e^x g:R->R i h(x)=||f(x)||^2 h:R^n->R. sad je g(x)=i(h(x)) a obje ove su difenercijabilne pa je Dg(x)=Di(h(x))Dh(x). lako se vidi da je Di(x)=e^x i Dh(x)=2x (ovo drugo se moze dokazat preko parcijalnih derivacija dosta lako ak ne vidis iz prve jer je h(x)=x_1^2+x_2^2+...+x_n^2) pa bi konacno rjesenje bilo
Dg(x)=e^(||f(x)||^2)*2f(x) (nadam se da nijesam fulao nigdje)
5. ovo je fora. teorem srednje vrijednosti kaze da za bilo koje tocke(vektore) x i y postoji tocka E na segmetnu x,y( naravno ako je fja definirana na cijelom segmentu, a ovdje ocito je) tako da je f(x)-f(y)=D(E)(x-y) a znas da je D(E)=A jer je to zadano u zadatku pa onda imas da za bilo koje x i y vrijedi f(x)-f(y)=Ax-Ay => f(x)-Ax=f(y)-Ay za bilo koje x i y iz R^n p taj izraz mora biti konstanta(i taj izraz je neki vektor iz R^m) pa to oznacimo s b i sad dobivas f(x)-Ax=b tj f(x)=Ax+b... ah, ovo je lijep zadatak 
6.gledaj fju korijen(x)..ako onda u tocki x_0 postize maksimum onda i funkcija f(x)=x postize u toj tockli maksimum jer ako postize u nekoj drugoj tocki y onda bi imao y=f(y)>=f(x)=x ali iz prve funkcije i maksimalnosti imas korijen(x)>=korijen(y) pa kad to kvadriras imas x>=y iz cega ide x=y.ista stvar za minimum.. eto tolko..treba sad ucit dalje za usmeni 
|
|
| [Vrh] |
|
buzov5
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
j.b.i.n.s.h.
Forumaš(ica)

Pridružen/a: 24. 06. 2007. (10:28:11)
Postovi: (1B)16
|
 Postano: 20:04 sub, 16. 2. 2008 Naslov: Postano: 20:04 sub, 16. 2. 2008 Naslov: |
    |
|
|
za sada se mogu uključiti samo u diskusiju vezanu za 2.zad
moje razmišljanje je ovako nekako:
znamo da neprekidna funkcija preslikava kompaktan skup u kompaktan, ali ne znamo mnogo o tome kakva je situacija u domeni ako je slika kompaktan skup
ne možemo govoriti o inverznoj funkciji ove funkcije jer nije injektivna, ali kad zaključimo da je [latex]f^{-1}([0,1]) [/latex] kugla u R2, tj {(x,y): [latex]x^{2}+y^{2}<=1 [/latex]} znamo da je taj skup ipak kompaktan
za sada se mogu uključiti samo u diskusiju vezanu za 2.zad
moje razmišljanje je ovako nekako:
znamo da neprekidna funkcija preslikava kompaktan skup u kompaktan, ali ne znamo mnogo o tome kakva je situacija u domeni ako je slika kompaktan skup
ne možemo govoriti o inverznoj funkciji ove funkcije jer nije injektivna, ali kad zaključimo da je 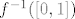 kugla u R2, tj {(x,y): kugla u R2, tj {(x,y): 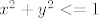 } znamo da je taj skup ipak kompaktan } znamo da je taj skup ipak kompaktan
_________________
...joined because i needed some help...
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 21:17 sub, 16. 2. 2008 Naslov: Postano: 21:17 sub, 16. 2. 2008 Naslov: |
    |
|
|
[quote="goc"]
6.gledaj fju korijen(x)..ako onda u tocki x_0 postize maksimum onda i funkcija f(x)=x postize u toj tockli maksimum jer ako postize u nekoj drugoj tocki y onda bi imao y=f(y)>=f(x)=x ali iz prve funkcije i maksimalnosti imas korijen(x)>=korijen(y) pa kad to kvadriras imas x>=y iz cega ide x=y.ista stvar za minimum.. eto tolko..treba sad ucit dalje za usmeni
[/quote]
goc je to fino formalno pokazao, ali dovoljno je reći da je funkcija korijen strogo monotona
(slikovito:
funkcija unutar korijena postiže svoje "sličice", korijen je strogo monoton i stoga će odnos sličica(odnos sličica = relacija "<=") funkcije korijen ostati isti kao i kod originala odnosno sličica funkcije unutar korijena (proizvoljne dvije sličice(funkcije unutar korijena) će i nakon djelovanja korijena ostati u relaciji "<="), osim što će doći do promjena vrijednosti.
Kako nas konkretne vrijednosti ekstrema ne zanimaju, već samo gdje se postižu, korijen možemo zanemariti i tražiti ekstreme funkcije unutar korijena)
Sada je potpuno jasno da je jednostavnije formalno pokazati, kako je goc napravio, nego opisati što se događa.
[quote="j.b.i.n.s.h."]za sada se mogu uključiti samo u diskusiju vezanu za 2.zad
moje razmišljanje je ovako nekako:
znamo da neprekidna funkcija preslikava kompaktan skup u kompaktan, ali ne znamo mnogo o tome kakva je situacija u domeni ako je slika kompaktan skup
ne možemo govoriti o inverznoj funkciji ove funkcije jer nije injektivna, ali kad zaključimo da je [latex]f^{-1}([0,1]) [/latex] kugla u R2, tj {(x,y): [latex]x^{2}+y^{2}<=1 [/latex]} znamo da je taj skup ipak kompaktan[/quote]
Tako je. Praslika segmenta [0,1] je zatvorena kugla oko nule radijusa 1, a taj skup je zatvoren i omeđen dakle kompaktan.
On je i povezan jer otvoren skup je povezan, ako se bilo koje dvije njegove točke mogu spojiti s konačno mnogo spojnica.
(definicija odnekud sa interneta(građevinski faks) :mrgreen: , ne pitaj što je spojnica, nek intuicija radi)
| goc (napisa): |
6.gledaj fju korijen(x)..ako onda u tocki x_0 postize maksimum onda i funkcija f(x)=x postize u toj tockli maksimum jer ako postize u nekoj drugoj tocki y onda bi imao y=f(y)>=f(x)=x ali iz prve funkcije i maksimalnosti imas korijen(x)>=korijen(y) pa kad to kvadriras imas x>=y iz cega ide x=y.ista stvar za minimum.. eto tolko..treba sad ucit dalje za usmeni
|
goc je to fino formalno pokazao, ali dovoljno je reći da je funkcija korijen strogo monotona
(slikovito:
funkcija unutar korijena postiže svoje "sličice", korijen je strogo monoton i stoga će odnos sličica(odnos sličica = relacija "⇐") funkcije korijen ostati isti kao i kod originala odnosno sličica funkcije unutar korijena (proizvoljne dvije sličice(funkcije unutar korijena) će i nakon djelovanja korijena ostati u relaciji "⇐"), osim što će doći do promjena vrijednosti.
Kako nas konkretne vrijednosti ekstrema ne zanimaju, već samo gdje se postižu, korijen možemo zanemariti i tražiti ekstreme funkcije unutar korijena)
Sada je potpuno jasno da je jednostavnije formalno pokazati, kako je goc napravio, nego opisati što se događa.
| j.b.i.n.s.h. (napisa): | za sada se mogu uključiti samo u diskusiju vezanu za 2.zad
moje razmišljanje je ovako nekako:
znamo da neprekidna funkcija preslikava kompaktan skup u kompaktan, ali ne znamo mnogo o tome kakva je situacija u domeni ako je slika kompaktan skup
ne možemo govoriti o inverznoj funkciji ove funkcije jer nije injektivna, ali kad zaključimo da je 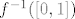 kugla u R2, tj {(x,y): kugla u R2, tj {(x,y): 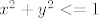 } znamo da je taj skup ipak kompaktan } znamo da je taj skup ipak kompaktan |
Tako je. Praslika segmenta [0,1] je zatvorena kugla oko nule radijusa 1, a taj skup je zatvoren i omeđen dakle kompaktan.
On je i povezan jer otvoren skup je povezan, ako se bilo koje dvije njegove točke mogu spojiti s konačno mnogo spojnica.
(definicija odnekud sa interneta(građevinski faks)  , ne pitaj što je spojnica, nek intuicija radi) , ne pitaj što je spojnica, nek intuicija radi)
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
buzov5
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 1:13 ned, 17. 2. 2008 Naslov: Postano: 1:13 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="buzov5"]a kako dokazat da f-ja opcenito ne preslikava kompaktan skup u kompaktan?
znam da ima TM da neprekidna preslikava, al kak ovo?[/quote]
npr:
[latex]f(x):= \{ \left { \begin{array}{} x \ ; \ x \neq 0 \\ 2 \ ; \ x=0 \end{array} \right [/latex] za koju vrijedi [latex]f([0,1])= \langle 0,1][/latex] , [latex]f^{-1}([0,1])= \langle 0,1][/latex]
EDIT: isprika :oops: na greški, kolega me ispravio post ispod
| buzov5 (napisa): | a kako dokazat da f-ja opcenito ne preslikava kompaktan skup u kompaktan?
znam da ima TM da neprekidna preslikava, al kak ovo? |
npr:
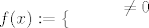 za koju vrijedi za koju vrijedi 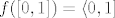 , , 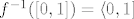
EDIT: isprika  na greški, kolega me ispravio post ispod na greški, kolega me ispravio post ispod
_________________
Rafael Mrđen
Zadnja promjena: rafaelm; 15:42 ned, 17. 2. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 9:24 ned, 17. 2. 2008 Naslov: Postano: 9:24 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="rafaelm"]
npr:
[latex]f(x):= \{ \left { \begin{array}{} x \ ; \ x \neq 0 \\ 2 \ ; \ x=0 \end{array} \right [/latex] za koju vrijedi [latex]f([0,1])= \langle 0,1][/latex] , [latex]f^{-1}([0,1])= \langle 0,1][/latex][/quote]
f([0,1]) = <0,1] U {2}
| rafaelm (napisa): |
npr:
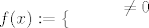 za koju vrijedi za koju vrijedi 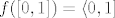 , , 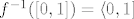 |
f([0,1]) = <0,1] U {2}
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
buzov5
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
 Postano: 12:17 ned, 17. 2. 2008 Naslov: Postano: 12:17 ned, 17. 2. 2008 Naslov: |
    |
|
|
hvala, hvala.
vidim da vam ide pa da vas udavim onako, do kraja..
ako je A lin op sa R^n u R^m.
sad ako kaze dokazite da je diferencijabilan i da mu je DL =L,
to znam, samo uvrstim u definiciju diferencijala.
a sta kad kaze odredite diferencijal? jel mogu napisat kandidat za
DL je L pa dokazat da to vrijedi ili moram kombinirat nes drugo?
mozda se nekom cini glupo al mene to sve smuvalo, nis ne kuzim.
hvala, hvala.
vidim da vam ide pa da vas udavim onako, do kraja..
ako je A lin op sa R^n u R^m.
sad ako kaze dokazite da je diferencijabilan i da mu je DL =L,
to znam, samo uvrstim u definiciju diferencijala.
a sta kad kaze odredite diferencijal? jel mogu napisat kandidat za
DL je L pa dokazat da to vrijedi ili moram kombinirat nes drugo?
mozda se nekom cini glupo al mene to sve smuvalo, nis ne kuzim.
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 12:44 ned, 17. 2. 2008 Naslov: Postano: 12:44 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="buzov5"]
a sta kad kaze odredite diferencijal? [/quote]
Kako je DL(x) = L , za svaki x@IR^n(linearno se najbolje aproksimira linearnim), odrediti diferencijal linearnog operatora u točki od nekog vektora(točka i vektor su dva različita naziva za isti objekt)znači odrediti vrijednost linearnog operatora od tog vektora.
Da bude jasnije,
DL(x) = L je jednakost funkcija
DL(x)(y) = L(y) je jednakost sličica tih funkcija
Valjda se moraju dati dvije točke da se konkretno odredi diferencijal, jedna je točka u kojoj se gleda diferencijal, točka x u DL(x), a druga je točka/vektor na koju diferencijal djeluje, recimo točka y pa imamo DL(x)(y). Stoga odrediti DL(x)(y) znači odrediti L(y), a on se odredi ako je L konkretno zadan.
| buzov5 (napisa): |
a sta kad kaze odredite diferencijal? |
Kako je DL(x) = L , za svaki x@IR^n(linearno se najbolje aproksimira linearnim), odrediti diferencijal linearnog operatora u točki od nekog vektora(točka i vektor su dva različita naziva za isti objekt)znači odrediti vrijednost linearnog operatora od tog vektora.
Da bude jasnije,
DL(x) = L je jednakost funkcija
DL(x)(y) = L(y) je jednakost sličica tih funkcija
Valjda se moraju dati dvije točke da se konkretno odredi diferencijal, jedna je točka u kojoj se gleda diferencijal, točka x u DL(x), a druga je točka/vektor na koju diferencijal djeluje, recimo točka y pa imamo DL(x)(y). Stoga odrediti DL(x)(y) znači odrediti L(y), a on se odredi ako je L konkretno zadan.
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
buzov5
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (13:30:32)
Postovi: (4D)16
Lokacija: zg
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 13:08 ned, 17. 2. 2008 Naslov: Postano: 13:08 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="buzov5"]
DL je L, ali kak doc do toga?[/quote]
Upravo to dokažeš, dakle da je DL = L.
To smo radili na vježbama, a i poviše si spomenuo rješenje, ukratko L je dfb funkcija ako limes iz definicije dfb-sti ide u nulu, treba ti kandidat za diferencijal pa uzmeš da je [b]L sam sebi kandidat[/b] i raspišeš.
Kad bolje razmislim u svom postu iznad sam te zbunio, od početka si znao odgovor. :wink:
| buzov5 (napisa): |
DL je L, ali kak doc do toga? |
Upravo to dokažeš, dakle da je DL = L.
To smo radili na vježbama, a i poviše si spomenuo rješenje, ukratko L je dfb funkcija ako limes iz definicije dfb-sti ide u nulu, treba ti kandidat za diferencijal pa uzmeš da je L sam sebi kandidat i raspišeš.
Kad bolje razmislim u svom postu iznad sam te zbunio, od početka si znao odgovor. 
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
goc9999
Forumaš(ica)


Pridružen/a: 15. 10. 2003. (19:31:20)
Postovi: (238)16
Spol: 
Lokacija: Utrina
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
 Postano: 13:26 ned, 17. 2. 2008 Naslov: Postano: 13:26 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="napraviculom"]ako se nekome da pogledat 4. zadatak s drugog kolokvija. nije mi jasno kako se dobije da je Hesseova matrica sedlasta. dobijem :
0 2y-1
2y-1 2x
i ako se uvrsti u (-1,1) se dobije
0 1
1 -2
nije li to sad negativno semidefinitna?
i jos nesto - ove permutacije, koje to smiju bit? samo zrcaljenje po sporednoj dijagonali ili sve? i sta "stoji" iza toga, zasto to smijemo radit?[/quote]
ne,ne
to je indefinitno
delta1=0
delta2=-1
to je indefinitna matrica
neg.semidef bi ti pocela sa -x,0,.. ili -x,y,0,...
kuzis?
| napraviculom (napisa): | ako se nekome da pogledat 4. zadatak s drugog kolokvija. nije mi jasno kako se dobije da je Hesseova matrica sedlasta. dobijem :
0 2y-1
2y-1 2x
i ako se uvrsti u (-1,1) se dobije
0 1
1 -2
nije li to sad negativno semidefinitna?
i jos nesto - ove permutacije, koje to smiju bit? samo zrcaljenje po sporednoj dijagonali ili sve? i sta "stoji" iza toga, zasto to smijemo radit? |
ne,ne
to je indefinitno
delta1=0
delta2=-1
to je indefinitna matrica
neg.semidef bi ti pocela sa -x,0,.. ili -x,y,0,...
kuzis?
|
|
| [Vrh] |
|
napraviculom
Forumaš(ica)

Pridružen/a: 01. 02. 2007. (16:40:37)
Postovi: (71)16
Spol: 
Lokacija: Scranton
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 13:36 ned, 17. 2. 2008 Naslov: Postano: 13:36 ned, 17. 2. 2008 Naslov: |
    |
|
|
[quote="goc"]
5. ovo je fora. teorem srednje vrijednosti kaze da za bilo koje tocke(vektore) x i y postoji tocka E na segmetnu x,y( naravno ako je fja definirana na cijelom segmentu, a ovdje ocito je) tako da je f(x)-f(y)=D(E)(x-y) a znas da je D(E)=A jer je to zadano u zadatku pa onda imas da za bilo koje x i y vrijedi f(x)-f(y)=Ax-Ay => f(x)-Ax=f(y)-Ay za bilo koje x i y iz R^n p taj izraz mora biti konstanta(i taj izraz je neki vektor iz R^m) pa to oznacimo s b i sad dobivas f(x)-Ax=b tj f(x)=Ax+b... ah, ovo je lijep zadatak :)
[/quote]
Mislim da te moram demantirat...naime Taylor (tj teorem srednje vrijednosti kojeg tu koristiš) se bavi realnim fjama, a tu imaš vektorsku (f ide u Rm) ;)
Ako sam u krivu, nek mene netko demantira
Vjerojatno ide na sličnu foru, al ne koristi se taj teorem
Moguće da se f gleda preko komponentnih fja...pa onda tm srednje vrijednosti za svaku komponentu posebno...recimo
| goc (napisa): |
5. ovo je fora. teorem srednje vrijednosti kaze da za bilo koje tocke(vektore) x i y postoji tocka E na segmetnu x,y( naravno ako je fja definirana na cijelom segmentu, a ovdje ocito je) tako da je f(x)-f(y)=D(E)(x-y) a znas da je D(E)=A jer je to zadano u zadatku pa onda imas da za bilo koje x i y vrijedi f(x)-f(y)=Ax-Ay ⇒ f(x)-Ax=f(y)-Ay za bilo koje x i y iz R^n p taj izraz mora biti konstanta(i taj izraz je neki vektor iz R^m) pa to oznacimo s b i sad dobivas f(x)-Ax=b tj f(x)=Ax+b... ah, ovo je lijep zadatak 
|
Mislim da te moram demantirat...naime Taylor (tj teorem srednje vrijednosti kojeg tu koristiš) se bavi realnim fjama, a tu imaš vektorsku (f ide u Rm) 
Ako sam u krivu, nek mene netko demantira
Vjerojatno ide na sličnu foru, al ne koristi se taj teorem
Moguće da se f gleda preko komponentnih fja...pa onda tm srednje vrijednosti za svaku komponentu posebno...recimo
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|

















