| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
 Postano: 10:17 sub, 12. 4. 2008 Naslov: Re: Par pitanja oko zadataka sa razvojem u Laurentov red Postano: 10:17 sub, 12. 4. 2008 Naslov: Re: Par pitanja oko zadataka sa razvojem u Laurentov red |
    |
|
|
hvala na odgovoru :)
[quote="Mr.Doe"][quote="rat in a cage"]Što točno znači boldano kad nam je zadano "Razvijte u Laurentov red funkciju oko nečega da [b]konvergira u a[/b]"
Ja sam shvatio da trebam odrediti vjenac na kojem ću razvijat u red tako da on ne pokupi nultočke nazivnika funkcije ali pokupi taj [i]a [/i]u koji konvergira. Jel to točno? :?: [/latex] [/quote]
Da. Mada ovaj komentar "ne pokupi nultocke nazivnika", bi ti mogao sugerirati krive stvari, npr. sta je nultocka nazivnika (meni omiljene :D ) gama funkcije [latex]\Gamma[/latex]?
[/quote]
ma da, no dobro. malo sam se slobodno izrazio jer sam gledao konkretan zadatak :oops:
[quote="Mr.Doe"]
[quote="rat in a cage"]
Kako razviti u Laurentov red funkciju:
[latex]f(z)=\frac{1}{z-1-i}[/latex] ako je [latex]|z|<2[/latex]
pokušavam i pokušavam i ne znam kako :cry:[/quote]
Ponovno nisi rekao oko koje tocke, pretpostavljam oko nule;
[/quote]
da oko 0, zaboravio sam napisat.
[quote="Mr.Doe"]
[latex]\displaystyle \frac{-1}{1+i}\cdot\frac{1}{1-\frac{z}{1+i}}[/latex], nadam se da mozes sam zavrsiti.[/quote]
tako sam i ja probao rastaviti, al kaj ne treba da bi se to moglo dalje razvit biti [latex]|\frac{z}{1+i}|<1[/latex]?
a ako je [latex]|z|<2\ [/latex] onda je [latex]\ |\frac{z}{1+i}|<\frac{2}{\sqrt{2}}[/latex] što je negdje 1.41 dakle nije manje od 1. :shock:
hvala na odgovoru 
| Mr.Doe (napisa): | | rat in a cage (napisa): | Što točno znači boldano kad nam je zadano "Razvijte u Laurentov red funkciju oko nečega da konvergira u a"
Ja sam shvatio da trebam odrediti vjenac na kojem ću razvijat u red tako da on ne pokupi nultočke nazivnika funkcije ali pokupi taj a u koji konvergira. Jel to točno?  [/latex] [/latex] |
Da. Mada ovaj komentar "ne pokupi nultocke nazivnika", bi ti mogao sugerirati krive stvari, npr. sta je nultocka nazivnika (meni omiljene  ) gama funkcije ) gama funkcije 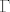 ? ?
|
ma da, no dobro. malo sam se slobodno izrazio jer sam gledao konkretan zadatak 
| Mr.Doe (napisa): |
| rat in a cage (napisa): |
Kako razviti u Laurentov red funkciju:
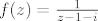 ako je ako je 
pokušavam i pokušavam i ne znam kako  |
Ponovno nisi rekao oko koje tocke, pretpostavljam oko nule;
|
da oko 0, zaboravio sam napisat.
| Mr.Doe (napisa): |
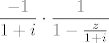 , nadam se da mozes sam zavrsiti. , nadam se da mozes sam zavrsiti. |
tako sam i ja probao rastaviti, al kaj ne treba da bi se to moglo dalje razvit biti 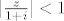 ? ?
a ako je  onda je onda je 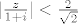 što je negdje 1.41 dakle nije manje od 1. što je negdje 1.41 dakle nije manje od 1. 
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 15:24 sub, 12. 4. 2008 Naslov: Re: Par pitanja oko zadataka sa razvojem u Laurentov red Postano: 15:24 sub, 12. 4. 2008 Naslov: Re: Par pitanja oko zadataka sa razvojem u Laurentov red |
    |
|
|
[quote="rat in a cage"]al kaj ne treba da bi se to moglo dalje razvit biti [latex]|\frac{z}{1+i}|<1[/latex]?
[/quote]
Pa i je, i tamo sam ja razvio funkciju u red potencija.
[quote="rat in a cage"]
a ako je [latex]|z|<2\ [/latex] onda je [latex]\ |\frac{z}{1+i}|<\frac{2}{\sqrt{2}}[/latex] što je negdje 1.41 dakle nije manje od 1. :shock:[/quote]
Ne razumijem sta si ovdje napisao..., idem ja probati korektno zadati zadatak;
Razvijte u Laurentov red oko točke [latex]z=0[/latex] funkciju;
[latex]f(z)=\frac{1}{z-1-i}[/latex], za tocke [latex]|z|<2[/latex].
I sada fino razvijes funkciju, tamo gdje uopce mozes, za [latex]|z|<|1+i|[/latex], u tockama [latex]|z|\geq |1+i|[/latex], red divergira.
Poanta je da ne mozes "natjerati" red da konvergira tamo gdje ti zelis.
| rat in a cage (napisa): | al kaj ne treba da bi se to moglo dalje razvit biti 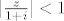 ? ?
|
Pa i je, i tamo sam ja razvio funkciju u red potencija.
| rat in a cage (napisa): |
a ako je  onda je onda je 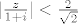 što je negdje 1.41 dakle nije manje od 1. što je negdje 1.41 dakle nije manje od 1.  |
Ne razumijem sta si ovdje napisao..., idem ja probati korektno zadati zadatak;
Razvijte u Laurentov red oko točke 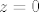 funkciju; funkciju;
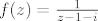 , za tocke , za tocke  . .
I sada fino razvijes funkciju, tamo gdje uopce mozes, za 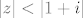 , u tockama , u tockama 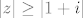 , red divergira. , red divergira.
Poanta je da ne mozes "natjerati" red da konvergira tamo gdje ti zelis.
|
|
| [Vrh] |
|
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
|
| [Vrh] |
|
|




