| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:38 pet, 11. 4. 2008 Naslov: kružnica x kružnica = torus ? Postano: 21:38 pet, 11. 4. 2008 Naslov: kružnica x kružnica = torus ? |
    |
|
|
Više puta sam čuo da je kartezijev produkt dvije kružnice [latex]S \times S[/latex] turus, u prostoru (untutrašnja guma od bicikle). Može li mi to netko obrazložiti...
[latex]S:= \{ (a,b) \in \mathbb{R}^{2} \ : \ a^{2}+b^{2}=1 \} \subseteq \mathbb{R}^{2}[/latex]
[latex]S \times S = \{ (s_{1},s_{2}) \ : \ s_{1},s_{2} \in S \} = \{ (x,y),(u,v)) \ : \ x^{2}+y^{2}=1, \ u^{2}+v^{2}=1 \} \cong \{(x,y,u,v) \ : \ x^{2}+y^{2}=u^{2}+v^{2}=1 \} \subseteq \mathbb{R}^{4}[/latex]
Zašto je to torus? Otkud opravdanje da se uopće može uložiti u 3D prostor?
Više puta sam čuo da je kartezijev produkt dvije kružnice 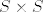 turus, u prostoru (untutrašnja guma od bicikle). Može li mi to netko obrazložiti... turus, u prostoru (untutrašnja guma od bicikle). Može li mi to netko obrazložiti...
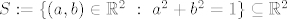
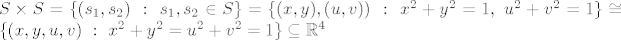
Zašto je to torus? Otkud opravdanje da se uopće može uložiti u 3D prostor?
_________________
Rafael Mrđen
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 1:45 sub, 12. 4. 2008 Naslov: Re: kružnica x kružnica = torus ? Postano: 1:45 sub, 12. 4. 2008 Naslov: Re: kružnica x kružnica = torus ? |
    |
|
|
[quote="rafaelm"]Zašto je to torus? Otkud opravdanje da se uopće može uložiti u 3D prostor?[/quote]
Torus, kao potprostor od [latex]\mathbb{R}^4[/latex], koji si ti opisao je homeomorfan s "3D torusom" T, potprostorom od [latex]\mathbb{R}^3[/latex], tj. postoji preslikavanje [latex]f \colon \mathbb{S}^1 \times \mathbb{S}^1 \to T \subset \mathbb{R}^3[/latex] koje je neprekidno, bijektivno i ima neprekidan inverz pa se i može uložiti u [latex]\mathbb{R}^3[/latex].
Za 3D torus T uzmemo prostor koji je dobiven rotiranjem malo sužene kružnice [latex]C_1[/latex] sa radijusom 1/2 i središtem u točki (1,0,0) oko z-osi. Neka je [latex]C_2[/latex] jedinična kružnica u xy ravnini. Znači, [latex]C_2[/latex] će biti i skup središta svih kružnica dobivenih rotiranjem kružnice [latex]C_1[/latex] oko z-osi. Uzimaju se [latex]C_1[/latex] i [latex]C_2[/latex] jer tada T baš liči na automobilsku gumu, dok središte od [latex]\mathbb{S}^1[/latex] je u ishodištu pa ne možemo to središte rotirati po rubu od [latex]\mathbb{S}^1[/latex] u xy ravnini. No i [latex]C_1[/latex] i [latex]C_2[/latex] su homeomorfni s [latex]\mathbb{S}^1[/latex] pa možemo i njihov produkt promatrati.
Sada je traženi homeomorfizam preslikavanje [latex]f \colon C_1 \times C_2 \to T[/latex] takvo da f(a,b) bude ona točka u koju se prenese [latex]a \in C_1[/latex] kada se središte od [latex]C_1[/latex] (koje se nalazi na [latex]C_2[/latex]) prenese u b.
| rafaelm (napisa): | | Zašto je to torus? Otkud opravdanje da se uopće može uložiti u 3D prostor? |
Torus, kao potprostor od 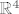 , koji si ti opisao je homeomorfan s "3D torusom" T, potprostorom od , koji si ti opisao je homeomorfan s "3D torusom" T, potprostorom od 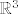 , tj. postoji preslikavanje , tj. postoji preslikavanje 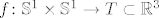 koje je neprekidno, bijektivno i ima neprekidan inverz pa se i može uložiti u koje je neprekidno, bijektivno i ima neprekidan inverz pa se i može uložiti u 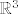 . .
Za 3D torus T uzmemo prostor koji je dobiven rotiranjem malo sužene kružnice 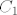 sa radijusom 1/2 i središtem u točki (1,0,0) oko z-osi. Neka je sa radijusom 1/2 i središtem u točki (1,0,0) oko z-osi. Neka je 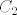 jedinična kružnica u xy ravnini. Znači, jedinična kružnica u xy ravnini. Znači, 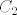 će biti i skup središta svih kružnica dobivenih rotiranjem kružnice će biti i skup središta svih kružnica dobivenih rotiranjem kružnice 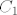 oko z-osi. Uzimaju se oko z-osi. Uzimaju se 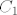 i i 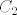 jer tada T baš liči na automobilsku gumu, dok središte od jer tada T baš liči na automobilsku gumu, dok središte od 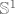 je u ishodištu pa ne možemo to središte rotirati po rubu od je u ishodištu pa ne možemo to središte rotirati po rubu od 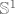 u xy ravnini. No i u xy ravnini. No i 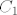 i i 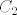 su homeomorfni s su homeomorfni s 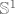 pa možemo i njihov produkt promatrati. pa možemo i njihov produkt promatrati.
Sada je traženi homeomorfizam preslikavanje 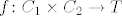 takvo da f(a,b) bude ona točka u koju se prenese takvo da f(a,b) bude ona točka u koju se prenese 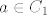 kada se središte od kada se središte od 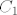 (koje se nalazi na (koje se nalazi na 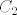 ) prenese u b. ) prenese u b.
_________________
The Dude Abides
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 9:37 sub, 12. 4. 2008 Naslov: Re: kružnica x kružnica = torus ? Postano: 9:37 sub, 12. 4. 2008 Naslov: Re: kružnica x kružnica = torus ? |
    |
|
|
[quote="goranm"]
Torus, kao potprostor od [latex]\mathbb{R}^4[/latex], koji si ti opisao je homeomorfan s "3D torusom" T, potprostorom od [latex]\mathbb{R}^3[/latex], tj. postoji preslikavanje [latex]f \colon \mathbb{S}^1 \times \mathbb{S}^1 \to T \subset \mathbb{R}^3[/latex] koje je neprekidno, bijektivno i ima neprekidan inverz pa se i može uložiti u [latex]\mathbb{R}^3[/latex].[/quote]
Znači li to da mi možemo reći da je [latex]C_1 \times C_2[/latex] bilo što, sve dok postoji homeomorfizam? Zar takvih skupova nema "puno", i to različitih?
npr. [latex]f \ : \ [0,1] \times [0,1] \to [0,2] \times [0,2], \ f(x,y)=(2x,2y)[/latex] mi djeluje kao homeomorfizam. A opet
[latex][0,1] \times [0,1][/latex] znamo da je[i] kocka[/i] sa stranicom 1, a ne 2...
edit: [i]kvadrat[/i]
| goranm (napisa): |
Torus, kao potprostor od 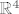 , koji si ti opisao je homeomorfan s "3D torusom" T, potprostorom od , koji si ti opisao je homeomorfan s "3D torusom" T, potprostorom od 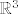 , tj. postoji preslikavanje , tj. postoji preslikavanje 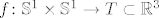 koje je neprekidno, bijektivno i ima neprekidan inverz pa se i može uložiti u koje je neprekidno, bijektivno i ima neprekidan inverz pa se i može uložiti u 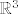 . . |
Znači li to da mi možemo reći da je 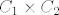 bilo što, sve dok postoji homeomorfizam? Zar takvih skupova nema "puno", i to različitih? bilo što, sve dok postoji homeomorfizam? Zar takvih skupova nema "puno", i to različitih?
npr. 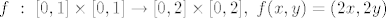 mi djeluje kao homeomorfizam. A opet mi djeluje kao homeomorfizam. A opet
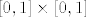 znamo da je kocka sa stranicom 1, a ne 2... znamo da je kocka sa stranicom 1, a ne 2...
edit: kvadrat
_________________
Rafael Mrđen
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 11:18 sub, 12. 4. 2008 Naslov: Re: kružnica x kružnica = torus ? Postano: 11:18 sub, 12. 4. 2008 Naslov: Re: kružnica x kružnica = torus ? |
    |
|
|
[quote="rafaelm"]Znači li to da mi možemo reći da je [latex]C_1 \times C_2[/latex] bilo što, sve dok postoji homeomorfizam? Zar takvih skupova nema "puno", i to različitih?[/quote]
Ako postoji homeomorfizam između dva topološka prostora X i Y, onda se oni smatraju "istima" u smislu da su se sva topološka svojstva od X putem homeomorfizma sačuvala u Y, ali i obratno. Homeomorfizam je analogon izomorfizmu, tj. izomorfizam čuva algebarsku, a homeomorfizam topološku strukturu. Svaki prostor može biti homeomorfan s puno drugih prostora, a homeomorfizam između dva prostora ne treba biti jedinstven. Poanta je da se neki prostor s kojim je teže raditi, tj. teško je za uočiti topološka svojstva, putem homeomorfizma (naravno, ako postoji) zamijeni nekim prostorom u kojemu se lakše uoče topološka svojstva.
[quote]
npr. [latex]f \ : \ [0,1] \times [0,1] \to [0,2] \times [0,2], \ f(x,y)=(2x,2y)[/latex] mi djeluje kao homeomorfizam. A opet
[latex][0,1] \times [0,1][/latex] znamo da je kocka sa stranicom 1, a ne 2...[/quote]
Da, to je homeomorfizam između dva kvadrata, bez obzira što su različite površine ili opsega. Zato se kaže da su homeomorfni (a ne isti), to jest jedan se može nekim preoblikovanjem dobiti iz drugog tako da se ne pokvare topološka svojstva. Tako da ako je [latex][0,2]\times [0,2][/latex] kompaktan, hausdorffov, metrizabilan itd. onda će to biti i [latex][0,1]\times [0,1][/latex].
| rafaelm (napisa): | Znači li to da mi možemo reći da je 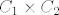 bilo što, sve dok postoji homeomorfizam? Zar takvih skupova nema "puno", i to različitih? bilo što, sve dok postoji homeomorfizam? Zar takvih skupova nema "puno", i to različitih? |
Ako postoji homeomorfizam između dva topološka prostora X i Y, onda se oni smatraju "istima" u smislu da su se sva topološka svojstva od X putem homeomorfizma sačuvala u Y, ali i obratno. Homeomorfizam je analogon izomorfizmu, tj. izomorfizam čuva algebarsku, a homeomorfizam topološku strukturu. Svaki prostor može biti homeomorfan s puno drugih prostora, a homeomorfizam između dva prostora ne treba biti jedinstven. Poanta je da se neki prostor s kojim je teže raditi, tj. teško je za uočiti topološka svojstva, putem homeomorfizma (naravno, ako postoji) zamijeni nekim prostorom u kojemu se lakše uoče topološka svojstva.
| Citat: |
npr. 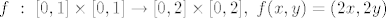 mi djeluje kao homeomorfizam. A opet mi djeluje kao homeomorfizam. A opet
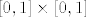 znamo da je kocka sa stranicom 1, a ne 2... znamo da je kocka sa stranicom 1, a ne 2... |
Da, to je homeomorfizam između dva kvadrata, bez obzira što su različite površine ili opsega. Zato se kaže da su homeomorfni (a ne isti), to jest jedan se može nekim preoblikovanjem dobiti iz drugog tako da se ne pokvare topološka svojstva. Tako da ako je 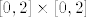 kompaktan, hausdorffov, metrizabilan itd. onda će to biti i kompaktan, hausdorffov, metrizabilan itd. onda će to biti i 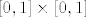 . .
_________________
The Dude Abides
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
|










