| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
 Postano: 23:31 čet, 17. 4. 2008 Naslov: teorem - l'hospitalovo pravilo Postano: 23:31 čet, 17. 4. 2008 Naslov: teorem - l'hospitalovo pravilo |
    |
|
|
pozdrav. htio bih nešto pitati u vezi s teoremom 4.17. iz skripte prof. guljaša. radi se o izrijeku i dokazu l'hospitalovog pravila. krenuo sam ga skuživati i primijetio sam da mi odmah u početku smeta nekoliko stvari.
(1) pretpostavka teorema je da f i g nisu definirane u c. to bi značilo da te funkcije nisu diferencijabilne u toj točki. ali, dokaz pravila koristi taylorov teorem srednje vrijednosti koji, štoviše, zahtijeva višestruku derivabilnost na cijelom intervalu pa i u c, kako bi bilo moguće uopće definirati taylorov polinom.
(2) i odmah ovdje mi je i druga nejasnoća u pretpostavci, odnosno, dokazu l'h-pravila: nigdje nije zahtijevano postojanje (n+1)-e derivacije, u ovom slučaju 2. derivacije funkcije f, odnosno, g koju zahtijeva taylorov teorem srednje vrijednosti.
može li mi netko reći što mi promiče u ovom teoremu da mi tako loše sjeda?
hvala
pozdrav. htio bih nešto pitati u vezi s teoremom 4.17. iz skripte prof. guljaša. radi se o izrijeku i dokazu l'hospitalovog pravila. krenuo sam ga skuživati i primijetio sam da mi odmah u početku smeta nekoliko stvari.
(1) pretpostavka teorema je da f i g nisu definirane u c. to bi značilo da te funkcije nisu diferencijabilne u toj točki. ali, dokaz pravila koristi taylorov teorem srednje vrijednosti koji, štoviše, zahtijeva višestruku derivabilnost na cijelom intervalu pa i u c, kako bi bilo moguće uopće definirati taylorov polinom.
(2) i odmah ovdje mi je i druga nejasnoća u pretpostavci, odnosno, dokazu l'h-pravila: nigdje nije zahtijevano postojanje (n+1)-e derivacije, u ovom slučaju 2. derivacije funkcije f, odnosno, g koju zahtijeva taylorov teorem srednje vrijednosti.
može li mi netko reći što mi promiče u ovom teoremu da mi tako loše sjeda?
hvala
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:02 pet, 18. 4. 2008 Naslov: Re: teorem - l'hospitalovo pravilo Postano: 0:02 pet, 18. 4. 2008 Naslov: Re: teorem - l'hospitalovo pravilo |
    |
|
|
[quote="PopStevo"]
(1) pretpostavka teorema je da f i g nisu definirane u c. to bi značilo da te funkcije nisu diferencijabilne u toj točki. ali, dokaz pravila koristi taylorov teorem srednje vrijednosti koji, štoviše, zahtijeva višestruku derivabilnost na cijelom intervalu pa i u c, kako bi bilo moguće uopće definirati taylorov polinom.[/quote]
Odmah na početku dokaza se komentira kako se dokaz provodi uz jače pretpostavke, tj. da fje. f i g imaju neprekidne derivacije na cijelom I i da je f(c)=g(c)=0 i g'(c)!=0.
| PopStevo (napisa): |
(1) pretpostavka teorema je da f i g nisu definirane u c. to bi značilo da te funkcije nisu diferencijabilne u toj točki. ali, dokaz pravila koristi taylorov teorem srednje vrijednosti koji, štoviše, zahtijeva višestruku derivabilnost na cijelom intervalu pa i u c, kako bi bilo moguće uopće definirati taylorov polinom. |
Odmah na početku dokaza se komentira kako se dokaz provodi uz jače pretpostavke, tj. da fje. f i g imaju neprekidne derivacije na cijelom I i da je f(c)=g(c)=0 i g'(c)!=0.
_________________
The Dude Abides
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
 Postano: 0:20 pet, 18. 4. 2008 Naslov: Postano: 0:20 pet, 18. 4. 2008 Naslov: |
    |
|
|
[quote="goranm"][quote="PopStevo"]
(1) pretpostavka teorema je da f i g nisu definirane u c. to bi značilo da te funkcije nisu diferencijabilne u toj točki. ali, dokaz pravila koristi taylorov teorem srednje vrijednosti koji, štoviše, zahtijeva višestruku derivabilnost na cijelom intervalu pa i u c, kako bi bilo moguće uopće definirati taylorov polinom.[/quote]
Odmah na početku dokaza se komentira kako se dokaz provodi uz jače pretpostavke, tj. da fje. f i g imaju neprekidne derivacije na cijelom I i da je f(c)=g(c)=0 i g'(c)!=0.[/quote]
ali, nije li dodatno potrebno da su i drugi put diferencijabilne, ne samo da imaju neprekidne prve derivacije (da bi se mogao primijeniti taylorov teorem srvr)?
[quote="goranm"][quote="PopStevo"](3) to što je [latex]g'(x)\neq 0, \forall x\in I\setminus {c}[/latex] ne mora značiti da je limes nazivnika [latex]\lim\limits_{x\to c}g'(x)=g'(c)\neq 0[/latex] pa mi ni posljednji korak dokaza nije jasan...
[/quote]
Nije mi baš jasno što želiš reći ovdje. Nazivnik je [latex]g'(c)-w_1(x)[/latex] pa je [latex]\lim\limits_{x\to c}(g'(c)-w_1(x))=g'(c)-\lim\limits_{x \to c} w_1 (x)=g'(c) \neq 0[/latex].[/quote]
ispričavam se, nisam u dokazu doživio izmjenu pretpostavke da je g'(c)!=0 :oops:
i ne bi li bilo elegantnije staviti pretpostavke u tvrdnju teorema?
| goranm (napisa): | | PopStevo (napisa): |
(1) pretpostavka teorema je da f i g nisu definirane u c. to bi značilo da te funkcije nisu diferencijabilne u toj točki. ali, dokaz pravila koristi taylorov teorem srednje vrijednosti koji, štoviše, zahtijeva višestruku derivabilnost na cijelom intervalu pa i u c, kako bi bilo moguće uopće definirati taylorov polinom. |
Odmah na početku dokaza se komentira kako se dokaz provodi uz jače pretpostavke, tj. da fje. f i g imaju neprekidne derivacije na cijelom I i da je f(c)=g(c)=0 i g'(c)!=0. |
ali, nije li dodatno potrebno da su i drugi put diferencijabilne, ne samo da imaju neprekidne prve derivacije (da bi se mogao primijeniti taylorov teorem srvr)?
| goranm (napisa): | | PopStevo (napisa): | (3) to što je 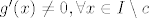 ne mora značiti da je limes nazivnika ne mora značiti da je limes nazivnika 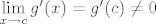 pa mi ni posljednji korak dokaza nije jasan... pa mi ni posljednji korak dokaza nije jasan...
|
Nije mi baš jasno što želiš reći ovdje. Nazivnik je 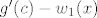 pa je pa je 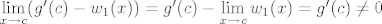 . . |
ispričavam se, nisam u dokazu doživio izmjenu pretpostavke da je g'(c)!=0 
i ne bi li bilo elegantnije staviti pretpostavke u tvrdnju teorema?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 2:00 pet, 18. 4. 2008 Naslov: Postano: 2:00 pet, 18. 4. 2008 Naslov: |
    |
|
|
[quote="PopStevo"]ali, nije li dodatno potrebno da su i drugi put diferencijabilne, ne samo da imaju neprekidne prve derivacije (da bi se mogao primijeniti taylorov teorem srvr)?[/quote]
Trenutno niti ja ne vidim da je to dovoljno. S obzirom da se koristi Taylorov teorem umjesto Cauchyevog, trebale bi biti i drugi put diferencijabilne. A s obzirom da se koristi i napomena 4.1, druge derivacije bi trebale biti i lokalno ograničene oko c. Da je rečeno da su druge derivacije neprekidne, onda bi se mogao iskoristiti i Taylorov teorem i napomena 4.1 jer je neprekidna funkcija u c i lokalno ograničena u c.
Cauchyev teorem srednje vrijednosti (mislim da je u skripti nazvan Lagrangeovim) daje puno jednostavniji dokaz, no ne znam da li su ekvivalentni.
| PopStevo (napisa): | | ali, nije li dodatno potrebno da su i drugi put diferencijabilne, ne samo da imaju neprekidne prve derivacije (da bi se mogao primijeniti taylorov teorem srvr)? |
Trenutno niti ja ne vidim da je to dovoljno. S obzirom da se koristi Taylorov teorem umjesto Cauchyevog, trebale bi biti i drugi put diferencijabilne. A s obzirom da se koristi i napomena 4.1, druge derivacije bi trebale biti i lokalno ograničene oko c. Da je rečeno da su druge derivacije neprekidne, onda bi se mogao iskoristiti i Taylorov teorem i napomena 4.1 jer je neprekidna funkcija u c i lokalno ograničena u c.
Cauchyev teorem srednje vrijednosti (mislim da je u skripti nazvan Lagrangeovim) daje puno jednostavniji dokaz, no ne znam da li su ekvivalentni.
_________________
The Dude Abides
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
amimica
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (15:40:42)
Postovi: (CA)16
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
|














