Deriviraš tu implicitno zadanu "funkciju" (staviš da je [latex]y=y(x)[/latex]) i dobiješ [latex]y'=\frac{-2x-y}{x+2y}[/latex]. To je koeficijent tangente u točki (x, y). Znači ako je [latex](x_0, y_0)[/latex] diralište, onda je jdba tangente (imamo točku i koeficijent smjera)
[latex]y-0=\frac{-2x_0-y_0}{x_0+2y_0} \cdot (x+2)[/latex]
Također i točka [latex](x_0, y_0)[/latex] leži na tom pravcu pa to uvrstimo i dobijemo
[latex]y_0-0=\frac{-2x_0-y_0}{x_0+2y_0} \cdot (x_0+2)[/latex]
tj.
[latex]y_0x_0+2y_0^2=-2x_0^2-4x_0-x_0y_0-2y_0[/latex] ekvivalentno s
[latex]2(y_0^2+x_0y_0+x_0^2)=-4x_0-2y_0[/latex]
Budući da je [latex](x_0, y_0)[/latex] na danoj krivulji, lijeva strana je jednaka 2, podijelimo s 2, rpebacimo i dobijemo [latex]y_0=-2x_0-1[/latex], sad to uvrstimo u [latex]x_0^2+x_0y_0+y_0^2=1[/latex], dobijemo jdbu [latex]3x_0(x_0+1)=0[/latex]. Izračunamo dirališta [latex](0, -1)[/latex] i [latex](-1, 1)[/latex] i sad lako dobimo tangente [latex]y=\frac{-x}{2}-1[/latex] i [latex]y=x+2[/latex]
Deriviraš tu implicitno zadanu "funkciju" (staviš da je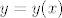 
) i dobiješ 
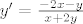. To je koeficijent tangente u točki (x, y). Znači ako je 
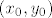diralište, onda je jdba tangente (imamo točku i koeficijent smjera)
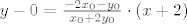
Također i točka 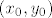leži na tom pravcu pa to uvrstimo i dobijemo
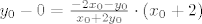
tj.
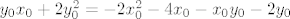ekvivalentno s
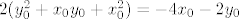
Budući da je 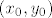na danoj krivulji, lijeva strana je jednaka 2, podijelimo s 2, rpebacimo i dobijemo 
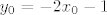, sad to uvrstimo u 
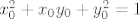, dobijemo jdbu 
. Izračunamo dirališta 
i 
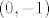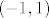i sad lako dobimo tangente 
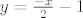i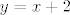 
_________________
Nikola Adžaga
Građevinski fakultet, Sveučilište u Zagrebu
