| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:16 ned, 1. 11. 2009 Naslov: Postano: 15:16 ned, 1. 11. 2009 Naslov: |
    |
|
|
[latex][1,2\rangle[/latex], ne [latex]\langle 1,2][/latex]. Razlika je minimalna, ali postoji, pogotovo za funkciju "najveće cijelo" :).
Misliš, odakle mi u smislu "kako si ga se sjetio" ili "zašto [latex][\sqrt{\frac{\pi}{2}},\sqrt{\pi}]\subseteq[1,2\rangle[/latex]"?
Odgovor na oba pitanja je dosta smislen. U prvom, pogledao sam što je najmanja moguća vrijednost od [latex]\sqrt{x}[/latex], a što je najveća. Utvrdio sam da su obje između [latex]1[/latex] i [latex]2[/latex], pa su i sve ostale vrijednosti od [latex]\sqrt{x}[/latex] između [latex]1[/latex] i [latex]2[/latex]. To mi jako odgovara jer onda znam da je najveće cijelo od svih njih upravo [latex]1[/latex]. Zapravo, cijeli moj odgovor bio je samo formalizacija rezultata ove motivacije.
U drugom pitanju, vrijedi [latex]\sqrt{\frac{\pi}{2}}\geq 1[/latex] (jer je to ekvivalentno s [latex]\pi\geq 2[/latex], a to stoji) i [latex]\sqrt{\pi}<2[/latex] (jer je to ekvivalentno s [latex]\pi<4[/latex], što također stoji). Rezultat je nakon toga očit.
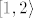 , ne , ne 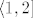 . Razlika je minimalna, ali postoji, pogotovo za funkciju "najveće cijelo" . Razlika je minimalna, ali postoji, pogotovo za funkciju "najveće cijelo"  . .
Misliš, odakle mi u smislu "kako si ga se sjetio" ili "zašto 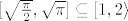 "? "?
Odgovor na oba pitanja je dosta smislen. U prvom, pogledao sam što je najmanja moguća vrijednost od 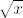 , a što je najveća. Utvrdio sam da su obje između , a što je najveća. Utvrdio sam da su obje između  i i  , pa su i sve ostale vrijednosti od , pa su i sve ostale vrijednosti od 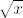 između između  i i  . To mi jako odgovara jer onda znam da je najveće cijelo od svih njih upravo . To mi jako odgovara jer onda znam da je najveće cijelo od svih njih upravo  . Zapravo, cijeli moj odgovor bio je samo formalizacija rezultata ove motivacije. . Zapravo, cijeli moj odgovor bio je samo formalizacija rezultata ove motivacije.
U drugom pitanju, vrijedi 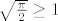 (jer je to ekvivalentno s (jer je to ekvivalentno s 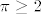 , a to stoji) i , a to stoji) i 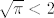 (jer je to ekvivalentno s (jer je to ekvivalentno s 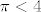 , što također stoji). Rezultat je nakon toga očit. , što također stoji). Rezultat je nakon toga očit.
Zadnja promjena: mornik; 15:19 ned, 1. 11. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
plonker
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (19:19:01)
Postovi: (8)16
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 17:28 ned, 1. 11. 2009 Naslov: Postano: 17:28 ned, 1. 11. 2009 Naslov: |
    |
|
|
@plonker (Mućke? :)): Napisao sam hint na prvoj stranici ovog very same topica :). Uglavnom, ideja je da pretpostaviš da [latex]f[/latex] nije injekcija i djeluješ s [latex]g[/latex] na ono što dobivaš. Onda dobivaš kontradikciju jer je [latex]\sinh[/latex] injektivna funkcija. Znam da ovo što sam sad rekao i nije baš najjasnije, pa javi ako treba još hintovlja.
@niveus: pretpostavljam da si uvidjela o kojoj se kompoziciji radi: [latex]f_1(x)=x^2+2x-2[/latex] i [latex]f_2(x)=\sin x[/latex] (mogu i neke druge funkcije, ali ovo mi se čini najprirodnije). Sad, ti znaš da je [latex]f^{-1}(x)=f_2^{-1}(f_1^{-1}(x))[/latex]. Prvo nas zanima funkcija inverzna [latex]f_1[/latex]. Pogledajmo prvo koliko je [latex]\mathcal{R}_f_2[/latex]. Zašto to gledamo, pitaš se :)? Jer želimo znati koji skup želimo da bude prirodna domena od [latex]f_1[/latex] (tj. u što da se preslika [latex]f_1^{-1}[/latex]). Lako vidimo da je [latex]\mathcal{R}_f_2=[-1,1][/latex]. Dakle, trebamo "namjestiti" [latex]f_1^{-1}[/latex] tako da daje vrijednosti u [latex][-1,1][/latex]. Sad znamo koji ćemo znak odabrati pri traženju inverza kvadratne funkcije i nemamo problema (javi ako imamo :)) s određivanjem: [latex]f_1^{-1}(x)=-1+\sqrt{3+x}[/latex], ako se ne varam.
Sad nas još zanima [latex]f_2^{-1}[/latex]. [url=http://degiorgi.math.hr/forum/viewtopic.php?t=13859&start=20]Tu[/url] sam napisao nešto na tu temu :). Dakle, "obični" arkus sinus nam ne odgovara jer on vraća vrijednosti u [latex][-\pi,\pi][/latex]. No, ako primijetimo da vrijedi [latex]\sin(x)=\sin(-\pi-x)[/latex] (a to lako dokažemo), tada smo na konju - naime, iz intervala [latex][-\frac{3\pi}{2},-\frac{\pi}{2}][/latex] "prelazimo" u [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]. Stoga, formalnije, funkciju [latex]f_2[/latex] možemo prikazati kao kompoziciju funkcija [latex]\sin x[/latex] (na intervalu [latex][-\frac{\pi}{2},\frac{\pi}{2}][/latex]) i [latex]-\pi-x[/latex]. Nakon toga nam nije teško: inverz od takvog "normalnog" sinusa je [latex]\arcsin x[/latex] a inverz od [latex]-\pi-x[/latex] je opet [latex]-\pi-x[/latex]. Komponiranjem ovoga dolazimo do [latex]f^{-1}(x)=-\pi-\arcsin(-1+\sqrt{3+x})[/latex], ako se ne varam.
@plonker (Mućke?  ): Napisao sam hint na prvoj stranici ovog very same topica ): Napisao sam hint na prvoj stranici ovog very same topica  . Uglavnom, ideja je da pretpostaviš da . Uglavnom, ideja je da pretpostaviš da  nije injekcija i djeluješ s nije injekcija i djeluješ s  na ono što dobivaš. Onda dobivaš kontradikciju jer je na ono što dobivaš. Onda dobivaš kontradikciju jer je 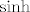 injektivna funkcija. Znam da ovo što sam sad rekao i nije baš najjasnije, pa javi ako treba još hintovlja. injektivna funkcija. Znam da ovo što sam sad rekao i nije baš najjasnije, pa javi ako treba još hintovlja.
@niveus: pretpostavljam da si uvidjela o kojoj se kompoziciji radi: 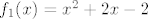 i i 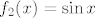 (mogu i neke druge funkcije, ali ovo mi se čini najprirodnije). Sad, ti znaš da je (mogu i neke druge funkcije, ali ovo mi se čini najprirodnije). Sad, ti znaš da je 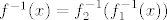 . Prvo nas zanima funkcija inverzna . Prvo nas zanima funkcija inverzna 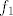 . Pogledajmo prvo koliko je . Pogledajmo prvo koliko je 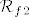 . Zašto to gledamo, pitaš se . Zašto to gledamo, pitaš se  ? Jer želimo znati koji skup želimo da bude prirodna domena od ? Jer želimo znati koji skup želimo da bude prirodna domena od 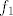 (tj. u što da se preslika (tj. u što da se preslika 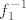 ). Lako vidimo da je ). Lako vidimo da je 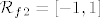 . Dakle, trebamo "namjestiti" . Dakle, trebamo "namjestiti" 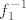 tako da daje vrijednosti u tako da daje vrijednosti u 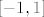 . Sad znamo koji ćemo znak odabrati pri traženju inverza kvadratne funkcije i nemamo problema (javi ako imamo . Sad znamo koji ćemo znak odabrati pri traženju inverza kvadratne funkcije i nemamo problema (javi ako imamo  ) s određivanjem: ) s određivanjem: 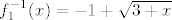 , ako se ne varam. , ako se ne varam.
Sad nas još zanima 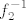 . Tu sam napisao nešto na tu temu . Tu sam napisao nešto na tu temu  . Dakle, "obični" arkus sinus nam ne odgovara jer on vraća vrijednosti u . Dakle, "obični" arkus sinus nam ne odgovara jer on vraća vrijednosti u 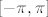 . No, ako primijetimo da vrijedi . No, ako primijetimo da vrijedi 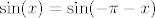 (a to lako dokažemo), tada smo na konju - naime, iz intervala (a to lako dokažemo), tada smo na konju - naime, iz intervala 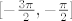 "prelazimo" u "prelazimo" u 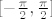 . Stoga, formalnije, funkciju . Stoga, formalnije, funkciju 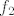 možemo prikazati kao kompoziciju funkcija možemo prikazati kao kompoziciju funkcija 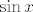 (na intervalu (na intervalu 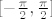 ) i ) i  . Nakon toga nam nije teško: inverz od takvog "normalnog" sinusa je . Nakon toga nam nije teško: inverz od takvog "normalnog" sinusa je 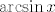 a inverz od a inverz od  je opet je opet  . Komponiranjem ovoga dolazimo do . Komponiranjem ovoga dolazimo do 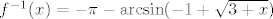 , ako se ne varam. , ako se ne varam.
|
|
| [Vrh] |
|
plonker
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (19:19:01)
Postovi: (8)16
|
|
| [Vrh] |
|
astrmastr
Forumaš(ica)

Pridružen/a: 30. 10. 2009. (23:45:28)
Postovi: (4)16
|
|
| [Vrh] |
|
jkrstic
Forumaš(ica)


Pridružen/a: 01. 10. 2009. (19:28:31)
Postovi: (AC)16
Spol: 
Lokacija: Somewhere in time
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:42 ned, 1. 11. 2009 Naslov: Postano: 19:42 ned, 1. 11. 2009 Naslov: |
    |
|
|
Točno, ako sam te dobro shvatio (imaš pravo, zbunjujuće je :lol:).
Na primjer, imaš [latex]f=f_1\circ f_2\circ f_3[/latex] i želiš odrediti [latex]f(A)[/latex] i [latex]f^{-1}(B)[/latex]. Tada imaš [latex]f(A)=f_1(f_2(f_3(A)))[/latex], što znači da prvo izračunaš [latex]f_3(A)[/latex], onda [latex]f_2(f_3(A))[/latex] i onda [latex]f_1(f_2(f_3(A)))[/latex].
Također, imaš [latex]f^{-1}(B)=f_3^{-1}(f_2^{-1}(f_1^{-1}(B)))[/latex]. Tada prvo računaš [latex]f_1^{-1}(B)[/latex], onda [latex]f_2^{-1}(f_1^{-1}(B))[/latex] i onda [latex]f_3^{-1}(f_2^{-1}(f_1^{-1}(B)))[/latex].
Točno, ako sam te dobro shvatio (imaš pravo, zbunjujuće je  ). ).
Na primjer, imaš 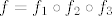 i želiš odrediti i želiš odrediti 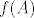 i i 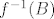 . Tada imaš . Tada imaš 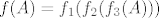 , što znači da prvo izračunaš , što znači da prvo izračunaš 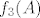 , onda , onda 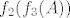 i onda i onda 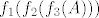 . .
Također, imaš 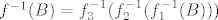 . Tada prvo računaš . Tada prvo računaš 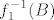 , onda , onda 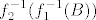 i onda i onda 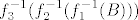 . .
|
|
| [Vrh] |
|
plonker
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (19:19:01)
Postovi: (8)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
mare
Forumaš(ica)

Pridružen/a: 01. 11. 2009. (20:20:21)
Postovi: (11)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
mare
Forumaš(ica)

Pridružen/a: 01. 11. 2009. (20:20:21)
Postovi: (11)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
|











