| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 15:41 sub, 1. 7. 2006 Naslov: Postano: 15:41 sub, 1. 7. 2006 Naslov: |
    |
|
|
[quote="Ignavia"]1. kod parcijalnog i potpunog pivotiranja smo napisali da nije potrebno izvrsiti zamjene redaka odnosno stupaca, nego samo pronadjemo doticni element u matrici s kojim hocemo ponistavat i onda bla bla...
hm, znaci dobijemo na kraju neku rupicastu matricu i da li nam je to sad neki problem? hocemo ju onda na kraju pretvorit u prekrasnu gornjetrokutastu ili nas to uopce ne zanima? ako ne, onda ce kompic stalno morat provjeravat i trazit di je nula di ne (kad rjesava sustav)? dal mi mozda nismo uopce obzirni prema kompicu? :cry:
[/quote]
Ne znam jesam dobro shvatio tvoje pitanje. Kad algoritam implementiramo u nekom programskom jeziku, onda ne izvršavamo zamjenu redaka (i stupaca kod potpunog pivotiranja), već vršimo indeksiranje preko vektora permutacije.
Evo primjera:
[latex]
PA=\left[
\begin{array}{ccc}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}
\right]\left[
\begin{array}{ccc}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{array}
\right] =
\left[
\begin{array}{ccc}
4 & 5 & 6 \\
1 & 2 & 3 \\
7 & 8 & 9
\end{array}
\right]
[/latex]
Matricu P zapamtimo kao vektor p=(2,1,3) (već imamo veliku uštedu prostora). I sad, kad želimo element [latex][PA]_{ij}[/latex] uzmemo element [latex][A]_{p_ij}[/latex]. Dakle, matrica PA nam uopće ne treba i ne treba je računati! :)
[quote="Ignavia"]
3. ona tri teorem- Faber, 2. i Weierstrass koje smo samo naveli trebaju i ostat samo navedeni il kaj? (dokaz?) (ovo je podmetnuto glupo pitanje)
[/quote]
Mislim da trebaju ostati nedokazani, da. Mene više zanima što je s teoremima u dijelu o Gaussovoj integraciji. Tamo pak ništa nije dokazano.
[quote="Ignavia"]
4. kakvu posebnu poruku nam salje Rungeov primjer? (u smislu Pn ne tezi ka f(x))
f(x)=1/1+x^2
[/quote]
Šalje nam poruku da se ne isplati povećavati stupanj interpolacijskog polinoma. Što veći stupanj polinoma uzmemo (na ekvidistantnoj mreži), mogla bi se dogoditi veća (a ne manja) greška!
| Ignavia (napisa): | 1. kod parcijalnog i potpunog pivotiranja smo napisali da nije potrebno izvrsiti zamjene redaka odnosno stupaca, nego samo pronadjemo doticni element u matrici s kojim hocemo ponistavat i onda bla bla...
hm, znaci dobijemo na kraju neku rupicastu matricu i da li nam je to sad neki problem? hocemo ju onda na kraju pretvorit u prekrasnu gornjetrokutastu ili nas to uopce ne zanima? ako ne, onda ce kompic stalno morat provjeravat i trazit di je nula di ne (kad rjesava sustav)? dal mi mozda nismo uopce obzirni prema kompicu? 
|
Ne znam jesam dobro shvatio tvoje pitanje. Kad algoritam implementiramo u nekom programskom jeziku, onda ne izvršavamo zamjenu redaka (i stupaca kod potpunog pivotiranja), već vršimo indeksiranje preko vektora permutacije.
Evo primjera:
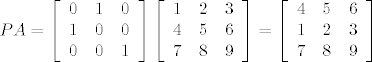
Matricu P zapamtimo kao vektor p=(2,1,3) (već imamo veliku uštedu prostora). I sad, kad želimo element 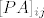 uzmemo element uzmemo element 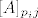 . Dakle, matrica PA nam uopće ne treba i ne treba je računati! . Dakle, matrica PA nam uopće ne treba i ne treba je računati! 
| Ignavia (napisa): |
3. ona tri teorem- Faber, 2. i Weierstrass koje smo samo naveli trebaju i ostat samo navedeni il kaj? (dokaz?) (ovo je podmetnuto glupo pitanje)
|
Mislim da trebaju ostati nedokazani, da. Mene više zanima što je s teoremima u dijelu o Gaussovoj integraciji. Tamo pak ništa nije dokazano.
| Ignavia (napisa): |
4. kakvu posebnu poruku nam salje Rungeov primjer? (u smislu Pn ne tezi ka f(x))
f(x)=1/1+x^2
|
Šalje nam poruku da se ne isplati povećavati stupanj interpolacijskog polinoma. Što veći stupanj polinoma uzmemo (na ekvidistantnoj mreži), mogla bi se dogoditi veća (a ne manja) greška!
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
zavod za analizu
Forumaš s poteškoćama u pisanju

Pridružen/a: 23. 06. 2006. (05:33:55)
Postovi: (5A)16
Spol: 
|
 Postano: 15:44 sub, 1. 7. 2006 Naslov: Postano: 15:44 sub, 1. 7. 2006 Naslov: |
    |
|
|
[quote="Ignavia"]
i evo jos malo pitanja za zavod pa i sire...
1. kod parcijalnog i potpunog pivotiranja smo napisali da nije potrebno izvrsiti zamjene redaka odnosno stupaca, nego samo pronadjemo doticni element u matrici s kojim hocemo ponistavat i onda bla bla...
hm, znaci dobijemo na kraju neku rupicastu matricu i da li nam je to sad neki problem? hocemo ju onda na kraju pretvorit u prekrasnu gornjetrokutastu ili nas to uopce ne zanima? ako ne, onda ce kompic stalno morat provjeravat i trazit di je nula di ne (kad rjesava sustav)? dal mi mozda nismo uopce obzirni prema kompicu? :cry: [/quote]
Zavod misli da je to dosta neobzirno prema kompicu. :x
[quote="Ignavia"]
2. dobili smo jednom za dz usporedit ocjenu pogreske kod Taylorovog i interpolacijskog polinoma u nultockama Cebisevljevog p., kak to tocno trebamo napravit - jasno je npr da kod interpol. imamo maksimum n+1-ve derivacije(tj. u nekoj tocki isto, al si malo zaokruzimo), a kod T. n+1-vu u nekoj tocki, (n+1)! i kod jednog i kod drugog, ali kaj cemo s ostatkom...
[/quote]
Hm. Zavod misli da ste na vježbama pokazali da za interpolacijski polinom u (translatiranim) Čebiševljevim točkama na [a,b] stupnja n funkcije f vrijedi slijedeća ocjena uniformne pogreške
[latex]\|f-p_n\|_{\infty}^{[a,b]}\leq \frac{(b-a)^{n+1}}{2^{2n+1}}\cdot \frac{M_{n+1}f}{(n+1)!}[/latex].
E sad, ako iskoristimo Taylorov teorem srednje vrijednosti, dobijemo slijedeću ocjenu unif. pogreške Taylorovim polinomom [latex]T_n[/latex]
[latex]\|f-T_n\|_{\infty}^{[a,b]}\leq (b-a)^{n+1}\cdot \frac{M_{n+1}f}{(n+1)!}[/latex].
Nakon poduže analize, zavodu se čini da prva ocjena izgleda bolje. :D 8)
[quote="Ignavia"]
3. ona tri teorem- Faber, 2. i Weierstrass koje smo samo naveli trebaju i ostat samo navedeni il kaj? (dokaz?) (ovo je podmetnuto glupo pitanje)
[/quote]
Ovo je ful dobro podmetnuto! :sherlock:
[quote="Ignavia"]
4. kakvu posebnu poruku nam salje Rungeov primjer? (u smislu Pn ne tezi ka f(x))
f(x)=1/1+x^2
[/quote]
Šalje nam dosta tužnu poruku. :cry: A to je da niz interpolacijskih polinoma na ekvidistanrnoj mreži ne mora unifomno konvergirati prema funkciji koju interpoliramo. A i ne mora se smanjivati ocjena pogreške povećanjem stupnja interpolacije. Dosta tužno. :cry: :cry:
[quote="Ignavia"]
5. sto je s Banachovim milim teoremom, pa to je najsvjetlija tocka, a nismo ni spomenuli na predavanjima? jel smo to mozda kojim slucajem dobili za zadacu bez da sam ja toga svijesna ili ne? opcenito rjesavanja nelinearnih jednadzbi ima samo 2 lista???
:band:[/quote]
Da nažalost, Zavodu je to isto najsvjetlija točka.
| Ignavia (napisa): |
i evo jos malo pitanja za zavod pa i sire...
1. kod parcijalnog i potpunog pivotiranja smo napisali da nije potrebno izvrsiti zamjene redaka odnosno stupaca, nego samo pronadjemo doticni element u matrici s kojim hocemo ponistavat i onda bla bla...
hm, znaci dobijemo na kraju neku rupicastu matricu i da li nam je to sad neki problem? hocemo ju onda na kraju pretvorit u prekrasnu gornjetrokutastu ili nas to uopce ne zanima? ako ne, onda ce kompic stalno morat provjeravat i trazit di je nula di ne (kad rjesava sustav)? dal mi mozda nismo uopce obzirni prema kompicu?  |
Zavod misli da je to dosta neobzirno prema kompicu. 
| Ignavia (napisa): |
2. dobili smo jednom za dz usporedit ocjenu pogreske kod Taylorovog i interpolacijskog polinoma u nultockama Cebisevljevog p., kak to tocno trebamo napravit - jasno je npr da kod interpol. imamo maksimum n+1-ve derivacije(tj. u nekoj tocki isto, al si malo zaokruzimo), a kod T. n+1-vu u nekoj tocki, (n+1)! i kod jednog i kod drugog, ali kaj cemo s ostatkom...
|
Hm. Zavod misli da ste na vježbama pokazali da za interpolacijski polinom u (translatiranim) Čebiševljevim točkama na [a,b] stupnja n funkcije f vrijedi slijedeća ocjena uniformne pogreške
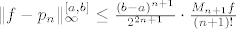 . .
E sad, ako iskoristimo Taylorov teorem srednje vrijednosti, dobijemo slijedeću ocjenu unif. pogreške Taylorovim polinomom 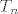
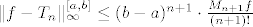 . .
Nakon poduže analize, zavodu se čini da prva ocjena izgleda bolje.  
| Ignavia (napisa): |
3. ona tri teorem- Faber, 2. i Weierstrass koje smo samo naveli trebaju i ostat samo navedeni il kaj? (dokaz?) (ovo je podmetnuto glupo pitanje)
|
Ovo je ful dobro podmetnuto! 
| Ignavia (napisa): |
4. kakvu posebnu poruku nam salje Rungeov primjer? (u smislu Pn ne tezi ka f(x))
f(x)=1/1+x^2
|
Šalje nam dosta tužnu poruku.  A to je da niz interpolacijskih polinoma na ekvidistanrnoj mreži ne mora unifomno konvergirati prema funkciji koju interpoliramo. A i ne mora se smanjivati ocjena pogreške povećanjem stupnja interpolacije. Dosta tužno. A to je da niz interpolacijskih polinoma na ekvidistanrnoj mreži ne mora unifomno konvergirati prema funkciji koju interpoliramo. A i ne mora se smanjivati ocjena pogreške povećanjem stupnja interpolacije. Dosta tužno.  
| Ignavia (napisa): |
5. sto je s Banachovim milim teoremom, pa to je najsvjetlija tocka, a nismo ni spomenuli na predavanjima? jel smo to mozda kojim slucajem dobili za zadacu bez da sam ja toga svijesna ili ne? opcenito rjesavanja nelinearnih jednadzbi ima samo 2 lista???
 |
Da nažalost, Zavodu je to isto najsvjetlija točka.
_________________ 
Zadnja promjena: zavod za analizu; 15:46 sub, 1. 7. 2006; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 16:20 sub, 1. 7. 2006 Naslov: Postano: 16:20 sub, 1. 7. 2006 Naslov: |
    |
|
|
Vauuu... pa nisam ocekivala da ste tako gladni :lol:
evo, svi dobijete sarme, al posto ne moze sve odjednom, prvi dobije goranm jer me je spasio iz pakla neimanja biljeski...
posto je vrlo komplicirano, ovdje cu napisati raspored sarmi:
[b]user[/b]____[b]ukupan broj sarmi[/b]___[b]Ignavia[/b]___[b]Grga[/b]
goranm__________4___________2_______2...... :klofam:
zavod__________2+2__________2_______2
Melkor__________2+1__________2_______1
Anđelčić________1+1__________1_______1
molim vas da sami pratite razvoj svojih sarmi, naknadne reklamacije (od pon nadalje) ne uvazavam :roll:
:elvis:
edit:
vsego__________3___________1,5______1,5
Vauuu... pa nisam ocekivala da ste tako gladni 
evo, svi dobijete sarme, al posto ne moze sve odjednom, prvi dobije goranm jer me je spasio iz pakla neimanja biljeski...
posto je vrlo komplicirano, ovdje cu napisati raspored sarmi:
user____ukupan broj sarmi___Ignavia___Grga
goranm__________4___________2_______2...... 
zavod__________2+2__________2_______2
Melkor__________2+1__________2_______1
Anđelčić________1+1__________1_______1
molim vas da sami pratite razvoj svojih sarmi, naknadne reklamacije (od pon nadalje) ne uvazavam 

edit:
vsego__________3___________1,5______1,5
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 11:19 ned, 2. 7. 2006 Naslov: Postano: 11:19 ned, 2. 7. 2006 Naslov: |
    |
|
|
ako ste slucajno pomislili da nemam vise pitanja... :lol:
1. odkud onih k! kod prosirenja definicije podijeljene razlike k-tog reda, ne, ne , ne mogu to nikako shvatit, izgleda da mi je odumrlo pola mozga ili tako nesto
2. teorem za Newtonovu metodu - u pretpostavkama teorema stoji f'(x0)*f''(x0)>0... i onda u dokazu razlikujemo 4 slucaja od kojih 2 ne zadovoljavaju tu pretpostavku??? hm? jel se to netko zeka?
3. ma onaj grozomorni tm (gauss-Legendrova bla bla) za koji je LSSD vec pitala, evo ponavljam pitanje dokaza, makar sam vec i na tom topicu pitala, tu je sve na jednom mjestu.
Dodjite po svoje sarme. :uncle_sam:
ako ste slucajno pomislili da nemam vise pitanja... 
1. odkud onih k! kod prosirenja definicije podijeljene razlike k-tog reda, ne, ne , ne mogu to nikako shvatit, izgleda da mi je odumrlo pola mozga ili tako nesto
2. teorem za Newtonovu metodu - u pretpostavkama teorema stoji f'(x0)*f''(x0)>0... i onda u dokazu razlikujemo 4 slucaja od kojih 2 ne zadovoljavaju tu pretpostavku??? hm? jel se to netko zeka?
3. ma onaj grozomorni tm (gauss-Legendrova bla bla) za koji je LSSD vec pitala, evo ponavljam pitanje dokaza, makar sam vec i na tom topicu pitala, tu je sve na jednom mjestu.
Dodjite po svoje sarme. 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 12:23 ned, 2. 7. 2006 Naslov: Postano: 12:23 ned, 2. 7. 2006 Naslov: |
    |
|
|
[quote="goranm"][quote="Ignavia"]2. teorem za Newtonovu metodu - u pretpostavkama teorema stoji f'(x0)*f''(x0)>0... i onda u dokazu razlikujemo 4 slucaja od kojih 2 ne zadovoljavaju tu pretpostavku??? hm? jel se to netko zeka?
[/quote]
U bilješkama stoji krivo, trebalo bi biti f(x0) * f''(x0)>0 umjesto f[size=18][b]'[/b][/size](x0)*f''(x0)>0
Ispričavam se :oops: , ja sam isto fotokopirao bilješke.
Taj teorem možeš pogledati na stranici 464 knjige.[/quote]
joj, ma super, hvala, sad mi je lakse :D
| goranm (napisa): | | Ignavia (napisa): | 2. teorem za Newtonovu metodu - u pretpostavkama teorema stoji f'(x0)*f''(x0)>0... i onda u dokazu razlikujemo 4 slucaja od kojih 2 ne zadovoljavaju tu pretpostavku??? hm? jel se to netko zeka?
|
U bilješkama stoji krivo, trebalo bi biti f(x0) * f''(x0)>0 umjesto f'(x0)*f''(x0)>0
Ispričavam se  , ja sam isto fotokopirao bilješke. , ja sam isto fotokopirao bilješke.
Taj teorem možeš pogledati na stranici 464 knjige. |
joj, ma super, hvala, sad mi je lakse 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 15:02 ned, 2. 7. 2006 Naslov: Postano: 15:02 ned, 2. 7. 2006 Naslov: |
    |
|
|
[quote="Ignavia"]1. odkud onih k! kod prosirenja definicije podijeljene razlike k-tog reda, ne, ne , ne mogu to nikako shvatit, izgleda da mi je odumrlo pola mozga ili tako nesto[/quote]
Ja si to objašnjavam ovako:
Neka je [latex]p_k[/latex] interpolacijski polinom stupnja k u točkama [latex]x_0,\ldots,x_k[/latex]. Želimo povećati stupanj interpolacije dodavanjem još jedne točke:
[latex]p_{k+1}(x)=p_k(x)+f[x_0,\ldots,x_{k+1}](x-x_0)\cdots(x-x_k)[/latex]
U točki [latex]x_{k+1}[/latex] vrijedi:
[latex]p_{k+1}(x_{k+1})=f(x_{k+1})=p_k(x_{k+1})+f[x_0,\ldots,x_{k+1}](x_{k+1}-x_0)\cdots(x_{k+1}-x_k)[/latex]
tj.
[latex]f(x_{k+1})-p_k(x_{k+1})=f[x_0,\ldots,x_{k+1}](x_{k+1}-x_0)\cdots(x_{k+1}-x_k)[/latex]
Sad to usporedimo s pogreškom interpolacijskog polinoma [latex]p_k[/latex] i dobivamo:
[latex]f[x_0,\ldots,x_{k+1}](x_{k+1}-x_0)\cdots(x_{k+1}-x_k)=\frac{f^{(k)}(\xi)}{k!}(x_{k+1}-x_0)\cdots(x_{k+1}-x_k)[/latex]
tj.
[latex]f[x_0,\ldots,x_{k+1}]=\frac{f^{(k)}(\xi)}{k!},\quad\xi\in\left<\min x_i,\max x_i\right>[/latex]
E, sad, kad bi "skupili" sve točke [latex]x_i[/latex] u [latex]x_0[/latex], onda bi i [latex]\xi[/latex] postao [latex]x_0[/latex] (k-ta derivacija od f je neprekidna). Pa tako lijepo proširimo definiciju podijeljene razlike.
| Ignavia (napisa): | | 1. odkud onih k! kod prosirenja definicije podijeljene razlike k-tog reda, ne, ne , ne mogu to nikako shvatit, izgleda da mi je odumrlo pola mozga ili tako nesto |
Ja si to objašnjavam ovako:
Neka je 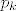 interpolacijski polinom stupnja k u točkama interpolacijski polinom stupnja k u točkama 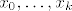 . Želimo povećati stupanj interpolacije dodavanjem još jedne točke: . Želimo povećati stupanj interpolacije dodavanjem još jedne točke:
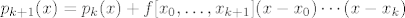
U točki 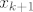 vrijedi: vrijedi:
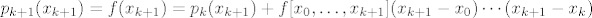
tj.
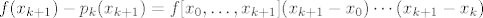
Sad to usporedimo s pogreškom interpolacijskog polinoma 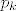 i dobivamo: i dobivamo:
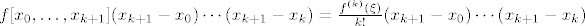
tj.
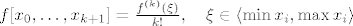
E, sad, kad bi "skupili" sve točke 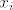 u u  , onda bi i , onda bi i 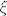 postao postao  (k-ta derivacija od f je neprekidna). Pa tako lijepo proširimo definiciju podijeljene razlike. (k-ta derivacija od f je neprekidna). Pa tako lijepo proširimo definiciju podijeljene razlike.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
Zadnja promjena: Melkor; 16:43 ned, 2. 7. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 20:01 ned, 2. 7. 2006 Naslov: Postano: 20:01 ned, 2. 7. 2006 Naslov: |
    |
|
|
@MB: Kolega MB, malo smo razočarani. :vatrica:
@zavod: s pravom, sramim se, jos sam se pravio pametan tu.. :oops:
@melkor: ovo "skupljanje" bi bilo preciznije objasnjeno s limesom (x_0,...x_n)->(x_0,...,x_0), ali svaka cast za ideju.
@MB: Kolega MB, malo smo razočarani. 
@zavod: s pravom, sramim se, jos sam se pravio pametan tu.. 
@melkor: ovo "skupljanje" bi bilo preciznije objasnjeno s limesom (x_0,...x_n)->(x_0,...,x_0), ali svaka cast za ideju.
|
|
| [Vrh] |
|
beros
Forumaš(ica)


Pridružen/a: 06. 11. 2002. (11:48:22)
Postovi: (29)16
|
 Postano: 20:05 pon, 3. 7. 2006 Naslov: Postano: 20:05 pon, 3. 7. 2006 Naslov: |
    |
|
|
[quote="goranm"]Pa gledajte, vrli Runge je bio ovako dosta ljubomoran tip i nije mogao podnjeti što Newton dobiva svu slavu pa je tako odlučio napraviti spačku. A kako ju je napravio? E tako da je osmislio taj svoj primjer koji "ima svojstvo da niz Newtonovih interpolacijskih polinoma na ekvidistantnoj mreži ne konvergira (po točkama) prema funkciji kada se broj čvorova povećava."
Strana 308, primjer 7.2.1 u udžbeniku numeričke analize.
Stvarno je zločest bio....
[/quote]
Žao mi je što kvarim veselje, ali ne postoji Newtonov interpolacijski polinom, postoji samo Newtonov oblik interpolacijskog polinoma (kao što postoji i Lagrangeov oblik interpolacijskog polinoma). Dakle, Runge nije imao zašto biti ljubomoran na Newtona ...
| goranm (napisa): | Pa gledajte, vrli Runge je bio ovako dosta ljubomoran tip i nije mogao podnjeti što Newton dobiva svu slavu pa je tako odlučio napraviti spačku. A kako ju je napravio? E tako da je osmislio taj svoj primjer koji "ima svojstvo da niz Newtonovih interpolacijskih polinoma na ekvidistantnoj mreži ne konvergira (po točkama) prema funkciji kada se broj čvorova povećava."
Strana 308, primjer 7.2.1 u udžbeniku numeričke analize.
Stvarno je zločest bio....
|
Žao mi je što kvarim veselje, ali ne postoji Newtonov interpolacijski polinom, postoji samo Newtonov oblik interpolacijskog polinoma (kao što postoji i Lagrangeov oblik interpolacijskog polinoma). Dakle, Runge nije imao zašto biti ljubomoran na Newtona ...
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 20:26 pon, 3. 7. 2006 Naslov: Postano: 20:26 pon, 3. 7. 2006 Naslov: |
    |
|
|
[quote="MB"]ovo "skupljanje" bi bilo preciznije objasnjeno s limesom (x_0,...x_n)->(x_0,...,x_0), ali svaka cast za ideju.[/quote]
Bilo bi, ali mislio sam da sam ionako pretjerao s količinom LaTeX-a u postu. :)
Inače, nije baš moja ideja, to sam pročitao u onoj on-line skripti Numerička analiza. :oops:
| MB (napisa): | | ovo "skupljanje" bi bilo preciznije objasnjeno s limesom (x_0,...x_n)→(x_0,...,x_0), ali svaka cast za ideju. |
Bilo bi, ali mislio sam da sam ionako pretjerao s količinom LaTeX-a u postu. 
Inače, nije baš moja ideja, to sam pročitao u onoj on-line skripti Numerička analiza. 
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 3:28 uto, 4. 7. 2006 Naslov: Postano: 3:28 uto, 4. 7. 2006 Naslov: |
    |
|
|
[quote="beros"][quote="goranm"]"ima svojstvo da niz Newtonovih interpolacijskih polinoma na ekvidistantnoj mreži ne konvergira (po točkama) prema funkciji kada se broj čvorova povećava."
Strana 308, primjer 7.2.1 u udžbeniku numeričke analize.
[/quote]
Žao mi je što kvarim veselje, ali ne postoji Newtonov interpolacijski polinom, postoji samo Newtonov oblik interpolacijskog polinoma (kao što postoji i Lagrangeov oblik interpolacijskog polinoma). Dakle, Runge nije imao zašto biti ljubomoran na Newtona ...[/quote]
To što sam u navodnike stavio je prepisano iz elektronskog udžbenika numeričke analize koji se nalazi na stranicama unm-a, možete pogledati na strani 308. :)
Ali slažem se, Newtonov je oblik :)
| beros (napisa): | | goranm (napisa): | "ima svojstvo da niz Newtonovih interpolacijskih polinoma na ekvidistantnoj mreži ne konvergira (po točkama) prema funkciji kada se broj čvorova povećava."
Strana 308, primjer 7.2.1 u udžbeniku numeričke analize.
|
Žao mi je što kvarim veselje, ali ne postoji Newtonov interpolacijski polinom, postoji samo Newtonov oblik interpolacijskog polinoma (kao što postoji i Lagrangeov oblik interpolacijskog polinoma). Dakle, Runge nije imao zašto biti ljubomoran na Newtona ... |
To što sam u navodnike stavio je prepisano iz elektronskog udžbenika numeričke analize koji se nalazi na stranicama unm-a, možete pogledati na strani 308. 
Ali slažem se, Newtonov je oblik 
_________________
The Dude Abides
|
|
| [Vrh] |
|
beros
Forumaš(ica)


Pridružen/a: 06. 11. 2002. (11:48:22)
Postovi: (29)16
|
|
| [Vrh] |
|
|

















