| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 20:49 pon, 31. 10. 2011 Naslov: Postano: 20:49 pon, 31. 10. 2011 Naslov: |
    |
|
|
b) Prvo računamo gustoću od [tex]Y - X[/tex]:[dtex]f_{Y - X}(z) = \int\limits_{-\infty}^{+\infty} \frac{1}{4} \mathbb{1}_{[-2, 2]}(x) \cdot \frac{1}{2 \sqrt{2 \pi}} e^{-\frac{(z + x)^2}{8}} dx = \int\limits_{-2}^{2} \frac{1}{8 \sqrt{2 \pi}} e^{-\frac{(z + x)^2}{8}} dx = \left[ \begin{array}{l}
t = \frac{z + x}{2} \\
dx = 2 dt
\end{array} \right] = \int\limits_{\frac{z}{2} - 1}^{\frac{z}{2} + 1} \frac{1}{4 \sqrt{2 \pi}} e^{-\frac{t^2}{2}} dt[/dtex]
Sad znamo da je [dtex]\mathbb{P}(X < Y) = \mathbb{P}(Y - X > 0) = \int\limits_0^{+\infty} f_{Y - X}(z) dz = \int\limits_0^{+\infty} \left( \int\limits_{\frac{z}{2} - 1}^{\frac{z}{2} + 1} \frac{1}{4 \sqrt{2 \pi}} e^{-\frac{t^2}{2}} dt \right) dz[/dtex]
Napravimo zamjenu poretka integracije (trebat će područje integracije podijeliti na dva dijela). Nakon malo petljanja ispadne rezultat [tex]\frac{1}{2}[/tex]. :w00t:
Ne vidim kako bi se ovo rješilo na drugačiji način, ali ako je netko uspio, rado bih znao. :D
c) Tu se iskoristi formula za gustoću produkta, napravi se supstitucija radi pojednostavljivanja, i stane se. Tako je u službenom rješenju. :D
b) Prvo računamo gustoću od [tex]Y - X[/tex]:[dtex]f_{Y - X}(z) = \int\limits_{-\infty}^{+\infty} \frac{1}{4} \mathbb{1}_{[-2, 2]}(x) \cdot \frac{1}{2 \sqrt{2 \pi}} e^{-\frac{(z + x)^2}{8}} dx = \int\limits_{-2}^{2} \frac{1}{8 \sqrt{2 \pi}} e^{-\frac{(z + x)^2}{8}} dx = \left[ \begin{array}{l}
t = \frac{z + x}{2} \\
dx = 2 dt
\end{array} \right] = \int\limits_{\frac{z}{2} - 1}^{\frac{z}{2} + 1} \frac{1}{4 \sqrt{2 \pi}} e^{-\frac{t^2}{2}} dt[/dtex]
Sad znamo da je [dtex]\mathbb{P}(X < Y) = \mathbb{P}(Y - X > 0) = \int\limits_0^{+\infty} f_{Y - X}(z) dz = \int\limits_0^{+\infty} \left( \int\limits_{\frac{z}{2} - 1}^{\frac{z}{2} + 1} \frac{1}{4 \sqrt{2 \pi}} e^{-\frac{t^2}{2}} dt \right) dz[/dtex]
Napravimo zamjenu poretka integracije (trebat će područje integracije podijeliti na dva dijela). Nakon malo petljanja ispadne rezultat [tex]\frac{1}{2}[/tex]. 
Ne vidim kako bi se ovo rješilo na drugačiji način, ali ako je netko uspio, rado bih znao. 
c) Tu se iskoristi formula za gustoću produkta, napravi se supstitucija radi pojednostavljivanja, i stane se. Tako je u službenom rješenju. 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:43 pon, 31. 10. 2011 Naslov: Postano: 22:43 pon, 31. 10. 2011 Naslov: |
    |
|
|
Fakat. #-o
E sad, ne znam jesi li to napravio namjerno, ili ti se potkrala greška. Treba integrirati zajedničku funkciju gustoće po skupu [latex]\{(x, y) \in \mathbb{R}^2 : x \in [-2, 2], y > x\}[/latex], a ti si dodao i 2 beskonačna trokuta na kojima ti se skratilo. Možda si drugačije razmišljao...
Fakat. 
E sad, ne znam jesi li to napravio namjerno, ili ti se potkrala greška. Treba integrirati zajedničku funkciju gustoće po skupu 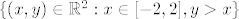 , a ti si dodao i 2 beskonačna trokuta na kojima ti se skratilo. Možda si drugačije razmišljao... , a ti si dodao i 2 beskonačna trokuta na kojima ti se skratilo. Možda si drugačije razmišljao...
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:12 pon, 31. 10. 2011 Naslov: Postano: 23:12 pon, 31. 10. 2011 Naslov: |
    |
|
|
Vidiš stvarno, a svejedno je ispalo dobro, imao sam sreće čini se.
Znači, trebalo bi onda razbiti na 3 integrala ili...?
Malo sam sad zbunjen, uopće nisam zapravo gledao po čem integriram,
više sam mehanički raspisao :D
Vidiš stvarno, a svejedno je ispalo dobro, imao sam sreće čini se.
Znači, trebalo bi onda razbiti na 3 integrala ili...?
Malo sam sad zbunjen, uopće nisam zapravo gledao po čem integriram,
više sam mehanički raspisao 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
čungalunga
Forumaš(ica)


Pridružen/a: 25. 11. 2009. (20:50:12)
Postovi: (4C)16
Spol: 
Lokacija: varaždin/zagreb
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|















