|
(To ćete inače na DIFRAF-u dokazivati za [latex]\mathbb{R}^n[/latex]. :))
Sljedeća tvrdnja će nam biti dovoljna: ako svaka okolina od [latex]\alpha\in\mathbb{R}[/latex] sadrži barem jedan član niza, a da je taj član različit od [latex]\alpha[/latex], onda je [latex]\alpha[/latex] gomilište niza. (Ovaj uvjet je očito "stroži" od tvog uvjeta, a zapravo lako možeš pokazati da su ta dva uvjeta ekvivalentna.)
Dokaz ide ovako: Uzmi sljedeći niz intervala (dakle, okolina): [latex]I_n=\langle \alpha-\displaystyle\frac{1}{n},\alpha+\frac{1}{n}\rangle[/latex] za sve [latex]n\in\mathbb{N}[/latex]. Sad, za svaki [latex]I_n\backslash \{\alpha\}[/latex] postoji neki [latex]a_{q(n)}[/latex] unutar tog skupa. Naš je problem sad što [latex]a_{q(n)}[/latex] nije nužno podniz (indeksi ne moraju biti rastući, a elementi se mogu i ponavljati). No dobro, to ćemo relativno lako riješiti:
Neka je [latex]a_{p(1)}=a_{q(1)}[/latex]. ([latex](a_{p(n)})_n[/latex] će nam biti traženi podniz.) Sad, tzv. jakom indukcijom (dakle, pretpostavljamo da tvrdnja vrijedi za sve [latex]1\leq k\leq n[/latex]) pretpostavimo da postoje elementi [latex]a_{p(k)}\in I_k\backslash \{\alpha\}[/latex]. Želimo tada pokazati i da možemo naći element [latex]a_{p(n+1)}\in I_{n+1}\backslash \{\alpha\}[/latex]. Pa dobro: neka je [latex]d=\min\{|a_{p(1)}-\alpha|, |a_{p(2)}-\alpha|, \ldots, |a_{p(n)}-\alpha|\}[/latex] - ovo što slijedi je relativno standardan trik. Znamo da je [latex]d>0[/latex] (jer nijedan od ovih elemenata nije [latex]\alpha[/latex]). Stoga, postoji neki [latex]t_0\in\mathbb{N}[/latex] takav da je [latex]\displaystyle\frac{1}{t_0}<d[/latex] (Arhimedov aksiom). Dapače, za sve [latex]t\geq t_0[/latex], [latex]t\in\mathbb{N}[/latex] vrijedi [latex]\displaystyle\frac{1}{t}<d[/latex].
E, sad, pogledajmo elemente [latex]a_{q(t)}[/latex] za [latex]t\geq t_0[/latex]. Nijedan od tih elemenata nije jednak nekom [latex]a_{p(k)}[/latex] "od gore". Naime, [latex]|a_{q(t)}-\alpha|<\displaystyle\frac{1}{t}\leq \frac{1}{t_0}<d=\min\{|a_{p(1)}-\alpha|, |a_{p(2)}-\alpha|, \ldots, |a_{p(n)}-\alpha|\}[/latex].
Sad, uzmimo [latex]f=\max\{t_0,p(n)\}[/latex]. Sad, ujedno znamo da [latex]a_f[/latex] nije jednak nijednom [latex]a_{p(k)}[/latex] za [latex]1\leq k\leq n[/latex] a i [latex]f>p(n)\geq n[/latex], pa je [latex]f\geq n+1[/latex]. Neka je sad [latex]a_{p(n+1)}:=a_f[/latex]: gotovi smo. :)
Naime, [latex]a_f\in\I_f\backslash\{\alpha\}[/latex], a kako je [latex]f\geq n+1[/latex], [latex]a_{p(n+1)}\in\I_{n+1}\backslash\{\alpha\}[/latex]. Stoga, završili smo korak indukcije.
Kako za članove podniza [latex](a_{p(n)})_n[/latex] vrijedi [latex]|a_{p(n)}-\alpha|<\displaystyle\frac{1}{n}[/latex], taj podniz uistinu konvergira u [latex]\alpha[/latex], pa smo gotovi.
Eto. Dokaz koji se radi u DIFRAF-u je sigurno elegantniji, ne sjećam ga se sad doslovno, ali ideja je ista. :) Ako nešto ne bude jasno, urlaj, ali to je u biti to. :)
(Ah, i pmli reče svoju riječ. :D Njegovo je zapravo jednostavnije jer ide direktno s tvojim uvjetom i nije glup kao ja. :P)
(To ćete inače na DIFRAF-u dokazivati za  . .  ) )
Sljedeća tvrdnja će nam biti dovoljna: ako svaka okolina od 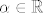 sadrži barem jedan član niza, a da je taj član različit od sadrži barem jedan član niza, a da je taj član različit od  , onda je , onda je  gomilište niza. (Ovaj uvjet je očito "stroži" od tvog uvjeta, a zapravo lako možeš pokazati da su ta dva uvjeta ekvivalentna.) gomilište niza. (Ovaj uvjet je očito "stroži" od tvog uvjeta, a zapravo lako možeš pokazati da su ta dva uvjeta ekvivalentna.)
Dokaz ide ovako: Uzmi sljedeći niz intervala (dakle, okolina): 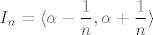 za sve za sve 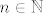 . Sad, za svaki . Sad, za svaki 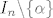 postoji neki postoji neki 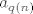 unutar tog skupa. Naš je problem sad što unutar tog skupa. Naš je problem sad što 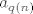 nije nužno podniz (indeksi ne moraju biti rastući, a elementi se mogu i ponavljati). No dobro, to ćemo relativno lako riješiti: nije nužno podniz (indeksi ne moraju biti rastući, a elementi se mogu i ponavljati). No dobro, to ćemo relativno lako riješiti:
Neka je 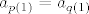 . ( . (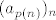 će nam biti traženi podniz.) Sad, tzv. jakom indukcijom (dakle, pretpostavljamo da tvrdnja vrijedi za sve će nam biti traženi podniz.) Sad, tzv. jakom indukcijom (dakle, pretpostavljamo da tvrdnja vrijedi za sve 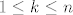 ) pretpostavimo da postoje elementi ) pretpostavimo da postoje elementi 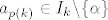 . Želimo tada pokazati i da možemo naći element . Želimo tada pokazati i da možemo naći element 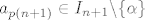 . Pa dobro: neka je . Pa dobro: neka je 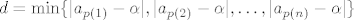 - ovo što slijedi je relativno standardan trik. Znamo da je - ovo što slijedi je relativno standardan trik. Znamo da je 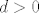 (jer nijedan od ovih elemenata nije (jer nijedan od ovih elemenata nije  ). Stoga, postoji neki ). Stoga, postoji neki 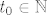 takav da je takav da je 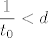 (Arhimedov aksiom). Dapače, za sve (Arhimedov aksiom). Dapače, za sve  , ,  vrijedi vrijedi 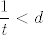 . .
E, sad, pogledajmo elemente 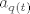 za za  . Nijedan od tih elemenata nije jednak nekom . Nijedan od tih elemenata nije jednak nekom 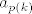 "od gore". Naime, "od gore". Naime, 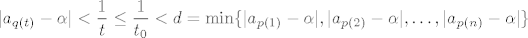 . .
Sad, uzmimo 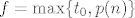 . Sad, ujedno znamo da . Sad, ujedno znamo da 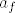 nije jednak nijednom nije jednak nijednom 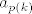 za za 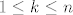 a i a i 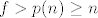 , pa je , pa je 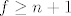 . Neka je sad . Neka je sad 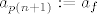 : gotovi smo. : gotovi smo. 
Naime, 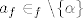 , a kako je , a kako je 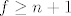 , , 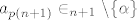 . Stoga, završili smo korak indukcije. . Stoga, završili smo korak indukcije.
Kako za članove podniza 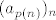 vrijedi vrijedi 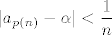 , taj podniz uistinu konvergira u , taj podniz uistinu konvergira u  , pa smo gotovi. , pa smo gotovi.
Eto. Dokaz koji se radi u DIFRAF-u je sigurno elegantniji, ne sjećam ga se sad doslovno, ali ideja je ista.  Ako nešto ne bude jasno, urlaj, ali to je u biti to. Ako nešto ne bude jasno, urlaj, ali to je u biti to. 
(Ah, i pmli reče svoju riječ.  Njegovo je zapravo jednostavnije jer ide direktno s tvojim uvjetom i nije glup kao ja. Njegovo je zapravo jednostavnije jer ide direktno s tvojim uvjetom i nije glup kao ja.  ) )
|




