| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 11:12 pon, 9. 10. 2006 Naslov: Postano: 11:12 pon, 9. 10. 2006 Naslov: |
    |
|
|
1. Teorem dualnosti u sparivanju
2. Euler-Lagrangeova jednadžba
3. Normalna jednadžba. Pravac regresije.
[quote]Hamiltonov princip, u koju kategoriju spada to pitanje, pod tesko ili lako pitanje??[/quote]
U ovogodišnjim predavanjima Hamiltonov princip je jedna jedina rečenica, ali se veže uz Euler-Lagrangeovu jednadžbu.
Evo da se službeno riješi misterij oko EL jednadžbe, to bi trebalo ići otprilike ovako:
Pretpostavimo da je položaj sistema opisan s r slobodnih koordinata
[latex]q=(q_1,\dots,q_r), \Phi (q) \in \mathbb{R}^{3N}[/latex] gdje je broj čestica (točaka) tog sistema.
Pretpostavimo da se sistem giba u polju sila F koje je konzervativno.
Potencijalnu energiju sistema označavamo s U(q).
Tražimo trajektorij (gibanje) [latex]t \mapsto q(t), \quad t \geq 0[/latex], t vrijeme.
Kako karakterizirati stvarnu putanju [latex]\gamma (t)[/latex] od svih mogućih ?
[latex]
t \mapsto q(t), \quad 0 \leq t < T \\
q(0)=A \quad q(T)=B \\
U(q(t)) \quad \textrm{potencijalna energija u trenutku t} \\
T(q(t), \dot{q}(t)) \quad \textrm{kineti\v{c}ka energija u trenutku t} \\
L(q,\dot{q})=T(q, \dot{q}) - U(q) \quad \textrm{Lagrangeova funkcija sistema}
[/latex]
[latex]
J(\gamma)=\int_0^T L(\gamma (t),\dot{\gamma} (t))dt
[/latex]
gdje je [latex]\gamma (t)[/latex] neka krivulja u U (područje karte U).
Stvarna krivulja je ona gdje [latex]J(\gamma (t))[/latex] poprima minimum.
Hamiltonov princip:
Od svih krivulja [latex]t \mapsto \gamma (t), \gamma (0)=A, \gamma (T)=B[/latex] stvarno gibanje sistema minimizira funkciju djelovanja [latex]J(\gamma)[/latex].
Teorem
Gibanje sistema [latex]t \mapsto \gamma (t)[/latex] je rješenje sistema diferencijalnih jednadžbi
[latex]
(1) \quad \frac{d}{dt} \left( \frac{ \partial L( q , \dot{q} )}{\partial \dot{q}_i} \right) - \frac{\partial L(q,\dot{q} ) }{\partial q_i} = 0, \quad i=1,\dots,r
[/latex]
(1) nazivamo Euler-Lagrangeovom jednadžbom.
Ako [latex]\gamma (t)[/latex] minimizira [latex]J(\gamma)[/latex], onda vrijedi (1).
Neka je [latex]\gamma[/latex] točka minimuma od [latex]J(\gamma)[/latex]. To znači da za svaku krivulju [latex]\gamma + \lambda \varphi, \quad \lambda \in \mathbb{R}, \varphi \in C_0^{\infty} (0,T), \varphi (0)=\varphi (T)=0[/latex] vrijedi:
[latex]J(\gamma + \lambda \varphi) \geq J(\gamma) \\
\displaystyle \lim_{n \to \infty} \frac{1}{\lambda}\left( J(\gamma + \lambda \varphi) - J(\gamma) \right) \geq 0
[/latex]
[latex]
0 \leq \displaystyle \lim_{n \to \infty} \frac{1}{\lambda}\left( \int_0^T( L (\gamma + \lambda \varphi, \dot{\gamma} + \lambda \dot{\varphi}) - L( \gamma, \dot{\gamma}))dt \right)[/latex]
[latex]
\displaystyle \lim_{n \to \infty} \frac{1}{\lambda} \textrm{ se ubaci pod integral i dobije se: }
[/latex]
[latex]
0=\int_0^T \left( \frac{\partial L(\gamma (t), \dot{\gamma} (t))}{\partial q} \varphi(t) + \frac{\partial L(\gamma(t), \dot{\gamma} (t))}{\partial \dot {q}} \dot{\varphi} (t)\right)dt
[/latex]
To se sada parcijalno integrira, iskoristi se osnovna lema varijacionog računa i dobije se (1).
:D
1. Teorem dualnosti u sparivanju
2. Euler-Lagrangeova jednadžba
3. Normalna jednadžba. Pravac regresije.
| Citat: | | Hamiltonov princip, u koju kategoriju spada to pitanje, pod tesko ili lako pitanje?? |
U ovogodišnjim predavanjima Hamiltonov princip je jedna jedina rečenica, ali se veže uz Euler-Lagrangeovu jednadžbu.
Evo da se službeno riješi misterij oko EL jednadžbe, to bi trebalo ići otprilike ovako:
Pretpostavimo da je položaj sistema opisan s r slobodnih koordinata
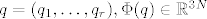 gdje je broj čestica (točaka) tog sistema. gdje je broj čestica (točaka) tog sistema.
Pretpostavimo da se sistem giba u polju sila F koje je konzervativno.
Potencijalnu energiju sistema označavamo s U(q).
Tražimo trajektorij (gibanje) 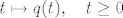 , t vrijeme. , t vrijeme.
Kako karakterizirati stvarnu putanju 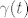 od svih mogućih ? od svih mogućih ?
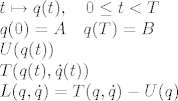
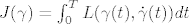
gdje je 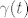 neka krivulja u U (područje karte U). neka krivulja u U (područje karte U).
Stvarna krivulja je ona gdje 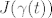 poprima minimum. poprima minimum.
Hamiltonov princip:
Od svih krivulja 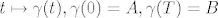 stvarno gibanje sistema minimizira funkciju djelovanja stvarno gibanje sistema minimizira funkciju djelovanja 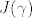 . .
Teorem
Gibanje sistema 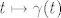 je rješenje sistema diferencijalnih jednadžbi je rješenje sistema diferencijalnih jednadžbi
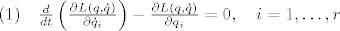
(1) nazivamo Euler-Lagrangeovom jednadžbom.
Ako 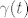 minimizira minimizira 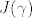 , onda vrijedi (1). , onda vrijedi (1).
Neka je 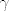 točka minimuma od točka minimuma od 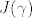 . To znači da za svaku krivulju . To znači da za svaku krivulju 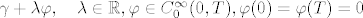 vrijedi: vrijedi:


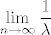
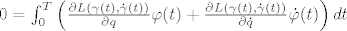
To se sada parcijalno integrira, iskoristi se osnovna lema varijacionog računa i dobije se (1).

_________________
The Dude Abides
|
|
| [Vrh] |
|
mickey
Forumaš(ica)

Pridružen/a: 02. 12. 2003. (14:34:02)
Postovi: (13)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Stormbringer
Forumaš(ica)
Pridružen/a: 20. 05. 2004. (21:38:56)
Postovi: (35)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 0:29 čet, 17. 12. 2009 Naslov: Postano: 0:29 čet, 17. 12. 2009 Naslov: |
    |
|
|
pa mislim da je dobar mail bio, ovaj na math, ne. hmmm, cak na matematici
to kao misteriozno sam ukomponirala adresu :blista:
ali samo se zezam malo, ne ocekujem vise da mi odgovori, a i nije vise vazno, sve je u redu! :D
pa mislim da je dobar mail bio, ovaj na math, ne. hmmm, cak na matematici
to kao misteriozno sam ukomponirala adresu 
ali samo se zezam malo, ne ocekujem vise da mi odgovori, a i nije vise vazno, sve je u redu! 
|
|
| [Vrh] |
|
Stormbringer
Forumaš(ica)
Pridružen/a: 20. 05. 2004. (21:38:56)
Postovi: (35)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Stormbringer
Forumaš(ica)
Pridružen/a: 20. 05. 2004. (21:38:56)
Postovi: (35)16
|
 Postano: 23:54 čet, 17. 12. 2009 Naslov: Postano: 23:54 čet, 17. 12. 2009 Naslov: |
    |
|
|
[quote="Ignavia"]
a zasto se ti dopisujes sa profesorom? nisam ranije htjela pitat jer je mozda nepristojno, ali sada se vec bolje poznamo :jastuk:[/quote]
LOL :D a što bi bila nepristojna, ionako mi se čini da smo izgleda samo ti i ja jedini preostali na ovom jalovom podforumu :D ja se dopisujem s profesorom, tj. dopisivao sam se, oko termina usmenog, koji je sad konačno ovaj ponedjeljak 8) moram priznat da je pomalo utješna spoznaja da ipak nisam ostalo jedan jedini, ubogi, individua odvojena od kolektivne svijesti apsolvenata koji su modeliranje davali prije 3 godine :oops: ovo je pretraumatična ispovijest....
| Ignavia (napisa): |
a zasto se ti dopisujes sa profesorom? nisam ranije htjela pitat jer je mozda nepristojno, ali sada se vec bolje poznamo  |
LOL  a što bi bila nepristojna, ionako mi se čini da smo izgleda samo ti i ja jedini preostali na ovom jalovom podforumu a što bi bila nepristojna, ionako mi se čini da smo izgleda samo ti i ja jedini preostali na ovom jalovom podforumu  ja se dopisujem s profesorom, tj. dopisivao sam se, oko termina usmenog, koji je sad konačno ovaj ponedjeljak ja se dopisujem s profesorom, tj. dopisivao sam se, oko termina usmenog, koji je sad konačno ovaj ponedjeljak  moram priznat da je pomalo utješna spoznaja da ipak nisam ostalo jedan jedini, ubogi, individua odvojena od kolektivne svijesti apsolvenata koji su modeliranje davali prije 3 godine moram priznat da je pomalo utješna spoznaja da ipak nisam ostalo jedan jedini, ubogi, individua odvojena od kolektivne svijesti apsolvenata koji su modeliranje davali prije 3 godine  ovo je pretraumatična ispovijest.... ovo je pretraumatična ispovijest....
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
Stormbringer
Forumaš(ica)
Pridružen/a: 20. 05. 2004. (21:38:56)
Postovi: (35)16
|
 Postano: 13:26 sub, 19. 12. 2009 Naslov: Postano: 13:26 sub, 19. 12. 2009 Naslov: |
    |
|
|
[quote="Ignavia"][quote="Stormbringer"]moram priznat da je pomalo utješna spoznaja da ipak nisam ostalo jedan jedini, ubogi, individua odvojena od kolektivne svijesti apsolvenata koji su modeliranje davali prije 3 godine [/quote]
da, to ipak nisi ti, nego ja. bas ti fala! :cestitam:
i pazi da ne padnes na ovom ledu vani na putu za ispit :voodoo: :zlobnik:[/quote]
hvala ti na lijepim željama, ipak, opasno će sklisko postati tek kad uđem u kabinet, upravo je nevjerojatno kako ovo predbožićno vrijeme ubija volju za učenje :oops:
| Ignavia (napisa): | | Stormbringer (napisa): | | moram priznat da je pomalo utješna spoznaja da ipak nisam ostalo jedan jedini, ubogi, individua odvojena od kolektivne svijesti apsolvenata koji su modeliranje davali prije 3 godine |
da, to ipak nisi ti, nego ja. bas ti fala! 
i pazi da ne padnes na ovom ledu vani na putu za ispit   |
hvala ti na lijepim željama, ipak, opasno će sklisko postati tek kad uđem u kabinet, upravo je nevjerojatno kako ovo predbožićno vrijeme ubija volju za učenje 
|
|
| [Vrh] |
|
Stormbringer
Forumaš(ica)
Pridružen/a: 20. 05. 2004. (21:38:56)
Postovi: (35)16
|
 Postano: 17:50 čet, 24. 12. 2009 Naslov: Postano: 17:50 čet, 24. 12. 2009 Naslov: |
    |
|
|
[quote="Ignavia"]
da, to ipak nisi ti, nego ja. bas ti fala! :cestitam:
[/quote]
emmm, probat ću ti ovo što nježnije priopćiti, ali da - mislim da si sad ostala sama na ovome :? ipaak, ako ti treba društvo ovdje na podforumu, mogu se ja zadržat još neko vrijeme ovdje :D
| Ignavia (napisa): |
da, to ipak nisi ti, nego ja. bas ti fala! 
|
emmm, probat ću ti ovo što nježnije priopćiti, ali da - mislim da si sad ostala sama na ovome  ipaak, ako ti treba društvo ovdje na podforumu, mogu se ja zadržat još neko vrijeme ovdje ipaak, ako ti treba društvo ovdje na podforumu, mogu se ja zadržat još neko vrijeme ovdje 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Stormbringer
Forumaš(ica)
Pridružen/a: 20. 05. 2004. (21:38:56)
Postovi: (35)16
|
 Postano: 21:01 pon, 28. 12. 2009 Naslov: Postano: 21:01 pon, 28. 12. 2009 Naslov: |
    |
|
|
[quote="goranm"][quote="Stormbringer"]emmm, probat ću ti ovo što nježnije priopćiti, ali da - mislim da si sad ostala sama na ovome :? ipaak, ako ti treba društvo ovdje na podforumu, mogu se ja zadržat još neko vrijeme ovdje :D[/quote]
opaaa...sad treba vidit tko će zadnji ostat na ma4 od nas dvojice :lol:[/quote]
hahaha, joooj da, još i to :oops: usput, tvoji materijali iz modeliranja su kod mene, vrlo rado ti to vratim, samo reci kad se sretnemo :)
| goranm (napisa): | | Stormbringer (napisa): | emmm, probat ću ti ovo što nježnije priopćiti, ali da - mislim da si sad ostala sama na ovome  ipaak, ako ti treba društvo ovdje na podforumu, mogu se ja zadržat još neko vrijeme ovdje ipaak, ako ti treba društvo ovdje na podforumu, mogu se ja zadržat još neko vrijeme ovdje  |
opaaa...sad treba vidit tko će zadnji ostat na ma4 od nas dvojice  |
hahaha, joooj da, još i to  usput, tvoji materijali iz modeliranja su kod mene, vrlo rado ti to vratim, samo reci kad se sretnemo usput, tvoji materijali iz modeliranja su kod mene, vrlo rado ti to vratim, samo reci kad se sretnemo 
|
|
| [Vrh] |
|
|











