| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:10 čet, 22. 11. 2007 Naslov: Relacije - konkretni primjer Postano: 12:10 čet, 22. 11. 2007 Naslov: Relacije - konkretni primjer |
    |
|
|
Dakle, jasno je meni "u teoriji" što su relacije, te znam definiciju...
No nije mi jasno npr, kako to upotrijebiti na nekom konkretnom primjeru, sa skupovima i elementima... Na primjer, DZ2, zadatak 4/a:
Provjerite odnos slijedećih skupove, dokažite relacije koje vrijede, a za one koje ne vrijede nađite kontraprimjer.
[latex]A \setminus(B \cup C)[/latex] i [latex](A \setminus B)\setminus C[/latex]
Ili kad su zadani elementi kao u 8. zadatku:
Na skupu [latex]S=\{1,2,3,4\}[/latex] zadana je relacija
[latex]\rho=\{(1,1),(1,5),(2,4),(3,1),(4,4),(5,1),(5,3)\}[/latex]
Proširite relaciju [latex]\rho[/latex] najmanjim brojem uređenih parova tako da bude refleksivna i simetrična relacija...
Pomoć itko :oops: ?
Dakle, jasno je meni "u teoriji" što su relacije, te znam definiciju...
No nije mi jasno npr, kako to upotrijebiti na nekom konkretnom primjeru, sa skupovima i elementima... Na primjer, DZ2, zadatak 4/a:
Provjerite odnos slijedećih skupove, dokažite relacije koje vrijede, a za one koje ne vrijede nađite kontraprimjer.
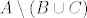 i i 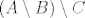
Ili kad su zadani elementi kao u 8. zadatku:
Na skupu 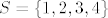 zadana je relacija zadana je relacija
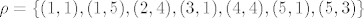
Proširite relaciju 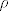 najmanjim brojem uređenih parova tako da bude refleksivna i simetrična relacija... najmanjim brojem uređenih parova tako da bude refleksivna i simetrična relacija...
Pomoć itko  ? ?
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
 Postano: 12:26 čet, 22. 11. 2007 Naslov: Postano: 12:26 čet, 22. 11. 2007 Naslov: |
    |
|
|
a ovo drugo imas neki skup od svejedno kolko elemenata,e sad da bi relacija bila refleksivna moras imati uredene parove koji to zadovoljavaju (npr. skup s elementima 1,2,3; relacija je refleksivna ako ima uredene parove (1,1),(2,2),(3,3)) i sad gledas kaj imas vec zadano u relaciji i nadopunjavas s onim kaj nemas a treba ti... isto tak i za simetricnost,tranzitivnost,antisimetricnost...
a ovo drugo imas neki skup od svejedno kolko elemenata,e sad da bi relacija bila refleksivna moras imati uredene parove koji to zadovoljavaju (npr. skup s elementima 1,2,3; relacija je refleksivna ako ima uredene parove (1,1),(2,2),(3,3)) i sad gledas kaj imas vec zadano u relaciji i nadopunjavas s onim kaj nemas a treba ti... isto tak i za simetricnost,tranzitivnost,antisimetricnost...
_________________
People are strange when you're a stranger...
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 12:26 čet, 22. 11. 2007 Naslov: Re: Relacije - konkretni primjer Postano: 12:26 čet, 22. 11. 2007 Naslov: Re: Relacije - konkretni primjer |
    |
|
|
[quote="punio4"]Dakle, jasno je meni "u teoriji" što su relacije, te znam definiciju...
No nije mi jasno npr, kako to upotrijebiti na nekom konkretnom primjeru, sa skupovima i elementima... Na primjer, DZ2, zadatak 4/a:
Provjerite odnos slijedećih skupove, dokažite relacije koje vrijede, a za one koje ne vrijede nađite kontraprimjer.
[latex]A \setminus(B \cup C)[/latex] i [latex](A \setminus B)\setminus C[/latex][/quote]
Ovako odokativno, rekao bih da su ti skupovi jednaki. 8)
[quote="punio4"]Ili kad su zadani elementi kao u 8. zadatku:
Na skupu [latex]S=\{1,2,3,4\}[/latex] zadana je relacija
[latex]\rho=\{(1,1),(1,5),(2,4),(3,1),(4,4),(5,1),(5,3)\}[/latex]
Proširite relaciju [latex]\rho[/latex] najmanjim brojem uređenih parova tako da bude refleksivna i simetrična relacija...[/quote]
Pa, dodaj parove koji fale. :D
Za refleksivnost, to su svi oblika [latex](x,x),\quad x \in S[/latex] (osim onih koje vec imas). :)
Za simetricnost, to su svi oblika [latex](y,x),\quad (x,y) \in \rho[/latex] (opet, osim onih koje vec imas). :)
Jasnije? :)
| punio4 (napisa): | Dakle, jasno je meni "u teoriji" što su relacije, te znam definiciju...
No nije mi jasno npr, kako to upotrijebiti na nekom konkretnom primjeru, sa skupovima i elementima... Na primjer, DZ2, zadatak 4/a:
Provjerite odnos slijedećih skupove, dokažite relacije koje vrijede, a za one koje ne vrijede nađite kontraprimjer.
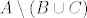 i i 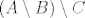 |
Ovako odokativno, rekao bih da su ti skupovi jednaki. 
| punio4 (napisa): | Ili kad su zadani elementi kao u 8. zadatku:
Na skupu 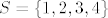 zadana je relacija zadana je relacija
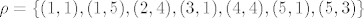
Proširite relaciju 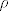 najmanjim brojem uređenih parova tako da bude refleksivna i simetrična relacija... najmanjim brojem uređenih parova tako da bude refleksivna i simetrična relacija... |
Pa, dodaj parove koji fale. 
Za refleksivnost, to su svi oblika  (osim onih koje vec imas). (osim onih koje vec imas). 
Za simetricnost, to su svi oblika 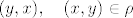 (opet, osim onih koje vec imas). (opet, osim onih koje vec imas). 
Jasnije? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
|











