| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
noa
Forumaš(ica)
Pridružen/a: 14. 04. 2007. (22:28:08)
Postovi: (51)16
|
|
| [Vrh] |
|
pins
Forumaš(ica)

Pridružen/a: 07. 12. 2006. (16:18:23)
Postovi: (17)16
|
|
| [Vrh] |
|
lyra
Forumaš(ica)

Pridružen/a: 17. 07. 2006. (21:23:44)
Postovi: (63)16
Spol: 
|
 Postano: 16:17 sri, 28. 11. 2007 Naslov: Postano: 16:17 sri, 28. 11. 2007 Naslov: |
    |
|
|
[quote="pins"]ajme ljudi, jedna grupa, je li bila (an+2)+3(an+1)-4(an)=12+10n rekurzija?? moguce je da mi se dogodija sramotan lapsus...[/quote]
hm..? da, bila je ta rekurzija..kaj s njom?
| pins (napisa): | | ajme ljudi, jedna grupa, je li bila (an+2)+3(an+1)-4(an)=12+10n rekurzija?? moguce je da mi se dogodija sramotan lapsus... |
hm..? da, bila je ta rekurzija..kaj s njom?
_________________
- Hey, Rachel, how many hipsters does it take to screw in a lightbulb?
- Gee, Jess, how many?
- You don't KNOW?
|
|
| [Vrh] |
|
pins
Forumaš(ica)

Pridružen/a: 07. 12. 2006. (16:18:23)
Postovi: (17)16
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
ft
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (21:38:47)
Postovi: (25)16
|
|
| [Vrh] |
|
ft
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (21:38:47)
Postovi: (25)16
|
 Postano: 19:32 sri, 28. 11. 2007 Naslov: Postano: 19:32 sri, 28. 11. 2007 Naslov: |
    |
|
|
Inace, evo rijesenje 8. iz moje grupe
Gledas jedan kvadrat 2x2 , npr onaj [ A22, A23, A32, A33] .
Za brojeve A22, A23, A32, A33 mora vrijediti :
A22 + A23 <= r ;
A22 + A32 <=r;
A23 + A33 <= r
A32 + A33 <= r;
Odnosno A22+ A23+ A32+ A33 <= 2r
Ali ako uvedemo jos uvjet da je A22+ A23+ A32+ A33 >= r stvari pocinju izgledati odlicno, jer je sada naime jednoznacno odredeno sto ostali brojevi u kvadratu 3x3 moraju biti.
Zasto ?
Jasno je kako dobijemo A21, A31, A12, A13. no jedini problem moze biti A11. ali ako pogledamo da je A12 + A13 = 2r – (A22+ A23+ A32+ A33) = A21 + A31 jasno je sada da je A11 isto jedinstveno odreden.
Dakle ukipan broj je u biti broj r<= A22+ A23+ A32+ A33 <= 2r uz 4 pocetna uvjeta, a to sada nije tesko izracunati.
E da mi je sada vratiti vrime, rijesija san ga u odma kuci. ima san tu ideju i na kolokviju samo je nesto zapelo pa san u nedostatku vrimena krenija na drugu ideju.
A to je ono sta ja uvik svima govorin, kad imas malo vrimena onda raste nervoza da neces stici sve rijesiti pa onda dolaze greske i koncentracija ti pada
Inace, evo rijesenje 8. iz moje grupe
Gledas jedan kvadrat 2x2 , npr onaj [ A22, A23, A32, A33] .
Za brojeve A22, A23, A32, A33 mora vrijediti :
A22 + A23 ⇐ r ;
A22 + A32 ⇐r;
A23 + A33 ⇐ r
A32 + A33 ⇐ r;
Odnosno A22+ A23+ A32+ A33 ⇐ 2r
Ali ako uvedemo jos uvjet da je A22+ A23+ A32+ A33 >= r stvari pocinju izgledati odlicno, jer je sada naime jednoznacno odredeno sto ostali brojevi u kvadratu 3x3 moraju biti.
Zasto ?
Jasno je kako dobijemo A21, A31, A12, A13. no jedini problem moze biti A11. ali ako pogledamo da je A12 + A13 = 2r – (A22+ A23+ A32+ A33) = A21 + A31 jasno je sada da je A11 isto jedinstveno odreden.
Dakle ukipan broj je u biti broj r⇐ A22+ A23+ A32+ A33 ⇐ 2r uz 4 pocetna uvjeta, a to sada nije tesko izracunati.
E da mi je sada vratiti vrime, rijesija san ga u odma kuci. ima san tu ideju i na kolokviju samo je nesto zapelo pa san u nedostatku vrimena krenija na drugu ideju.
A to je ono sta ja uvik svima govorin, kad imas malo vrimena onda raste nervoza da neces stici sve rijesiti pa onda dolaze greske i koncentracija ti pada
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 19:39 sri, 28. 11. 2007 Naslov: Postano: 19:39 sri, 28. 11. 2007 Naslov: |
    |
|
|
Ajde ajde ft, bit će 100% na drugom kolokviju, bit će 5 iz diskretne, ne brini...znamo mi svi da ti to znaš... :tapsh:
@Ronnie Ja sam razmišljao ovak: biram prvi par na 150*100 načina, drugi na 149*99 i tako do 131*81 i sve to podijelim sa 20! jer mi nije bitan poredak parova. Kad se to sredi dobiju se oni povrsi i 20!
Ajde ajde ft, bit će 100% na drugom kolokviju, bit će 5 iz diskretne, ne brini...znamo mi svi da ti to znaš... 
@Ronnie Ja sam razmišljao ovak: biram prvi par na 150*100 načina, drugi na 149*99 i tako do 131*81 i sve to podijelim sa 20! jer mi nije bitan poredak parova. Kad se to sredi dobiju se oni povrsi i 20!
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
Zadnja promjena: Luuka; 19:41 sri, 28. 11. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
pucca
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (19:23:02)
Postovi: (1B)16
Lokacija: Osijek
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 19:54 sri, 28. 11. 2007 Naslov: Postano: 19:54 sri, 28. 11. 2007 Naslov: |
    |
|
|
sve je ok, ft, vjerujemo ti mi da si ti to riješio doma, ne moraš nam to dokazivat ovim putem ;)
ajd sad za izazov riješi 8. zadatak iz druge grupe, onaj sa sumom produkata rješenja jednadžbe... ak ne znaš kak točno ide, pitaj, budem ti rekla :)
sve je ok, ft, vjerujemo ti mi da si ti to riješio doma, ne moraš nam to dokazivat ovim putem 
ajd sad za izazov riješi 8. zadatak iz druge grupe, onaj sa sumom produkata rješenja jednadžbe... ak ne znaš kak točno ide, pitaj, budem ti rekla 
_________________ kalendar 
  |
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
 Postano: 20:59 sri, 28. 11. 2007 Naslov: Postano: 20:59 sri, 28. 11. 2007 Naslov: |
    |
|
|
hm....nisam ga jos do kraja piknuo, al cini se da je rjesenje [latex]{n+k-1}\choose{n-k}[/latex]
nisam ga rjesavao slazuci neke bijekcije nego algebarski vise, al mozda sad nekom sine ideja kad vidi broj :)
inace, jel ima jos ko tupav poput mene da je uspio sat vremena rjesavat rekurziju a da ju NIJE rijesio do kraja :) 2.-7. nam nisu bili preteski, zadnji izgleda cist pristojno...
EDIT:rjesenje je to sto sam reko [latex]{n+k-1}\choose{n-k}[/latex] ili [latex]{n+k-1}\choose{2k-1}[/latex], kad to pogodite(ne pitajte kako :) )bacite jaku indukciju i podijelite malo na slucajeve:
ukratko: oznacimo s [latex]f(n,k)[/latex] trazenu sumu za svaki n i k. ako bi n_1 bio jednak tocno jedan onda kad gledamo ostale cemo imat [latex]f(n-1,k-1)[/latex] sto mnozimo sa svima zajednickim faktorom 1
ako bi n_1 bio tocno dva onda za ostale imamo [latex]f(n-2,k-1)[/latex] sto mnozimo sa zajednickim faktorom 2... itd...
ako ib n_1 bio tocno [latex](n-k+1)[/latex] (a to je maksimalna vrijednost da bi i svi ostali mogli biti prirodni) onda ostale rasporedimo na [latex]f(k-1,k-1)[/latex] i mnozimo s [latex]n-k+1[/latex]
sad imamo
[latex]f(n,k)=\sum_{i=1}^{n-k+1} i*f(n-i,k-1)[/latex]=
[latex]\sum_{i=1}^{n-k+1} i\cdot[/latex] [latex]n+k-i-2\choose2k-3[/latex]
ok. sad ovo raspisete u niz suma...nesto ovakvo
[latex]2k-3\choose2k-3[/latex]
[latex]2k-3\choose2k-3[/latex] + [latex]2k-2\choose2k-3[/latex]
[latex]2k-3\choose2k-3[/latex] + [latex]2k-2\choose2k-2[/latex] + [latex]2k-1\choose2k-3[/latex] itd...
suma u svakom retku je jednaka
[latex]2k-2\choose2k-2[/latex]
[latex]2k-1\choose2k-2[/latex]
[latex]2k\choose2k-2[/latex] itd.. do
[latex]n+k-2\choose2k-2[/latex]
suma svega toga je
[latex]n+k-1\choose2k-1[/latex] sto smo i htjeli dokazati...
bla
sad se mogu posvetit zlom SPAu...(nadam se da me vsego nece zbog ovog komentara zadav't :) )
hm....nisam ga jos do kraja piknuo, al cini se da je rjesenje 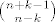
nisam ga rjesavao slazuci neke bijekcije nego algebarski vise, al mozda sad nekom sine ideja kad vidi broj 
inace, jel ima jos ko tupav poput mene da je uspio sat vremena rjesavat rekurziju a da ju NIJE rijesio do kraja  2.-7. nam nisu bili preteski, zadnji izgleda cist pristojno... 2.-7. nam nisu bili preteski, zadnji izgleda cist pristojno...
EDIT:rjesenje je to sto sam reko 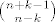 ili ili 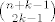 , kad to pogodite(ne pitajte kako , kad to pogodite(ne pitajte kako  )bacite jaku indukciju i podijelite malo na slucajeve: )bacite jaku indukciju i podijelite malo na slucajeve:
ukratko: oznacimo s 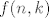 trazenu sumu za svaki n i k. ako bi n_1 bio jednak tocno jedan onda kad gledamo ostale cemo imat trazenu sumu za svaki n i k. ako bi n_1 bio jednak tocno jedan onda kad gledamo ostale cemo imat 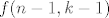 sto mnozimo sa svima zajednickim faktorom 1 sto mnozimo sa svima zajednickim faktorom 1
ako bi n_1 bio tocno dva onda za ostale imamo 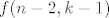 sto mnozimo sa zajednickim faktorom 2... itd... sto mnozimo sa zajednickim faktorom 2... itd...
ako ib n_1 bio tocno 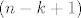 (a to je maksimalna vrijednost da bi i svi ostali mogli biti prirodni) onda ostale rasporedimo na (a to je maksimalna vrijednost da bi i svi ostali mogli biti prirodni) onda ostale rasporedimo na 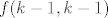 i mnozimo s i mnozimo s 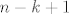
sad imamo
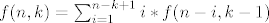 = =
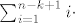 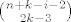
ok. sad ovo raspisete u niz suma...nesto ovakvo
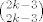
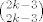 + + 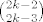
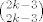 + + 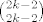 + + 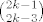 itd... itd...
suma u svakom retku je jednaka
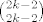
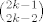
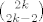 itd.. do itd.. do
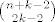
suma svega toga je
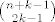 sto smo i htjeli dokazati... sto smo i htjeli dokazati...
bla
sad se mogu posvetit zlom SPAu...(nadam se da me vsego nece zbog ovog komentara zadav't  ) )
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
Nori
Forumaš(ica)
Pridružen/a: 01. 10. 2006. (18:41:07)
Postovi: (E5)16
Spol: 
|
 Postano: 21:53 sri, 28. 11. 2007 Naslov: Postano: 21:53 sri, 28. 11. 2007 Naslov: |
    |
|
|
Ja se slažem s ft-om. Bila sam tvoja grupa, i u najmnanju ruku, kolokvij je bio neprimjeren (barem naša grupa)...
Ti ciklusi permutacija, taj dokaz ide prek cijele strane i više, užasno puno posla, zatim taj s 2 okrugla stola, 12 345 ljudi, i 2 uvjeta i zadnji koji je nerješiv u pola sata, sat za ljude inteligencije<150 čine kolokvij teškim:((((
Ja se slažem s ft-om. Bila sam tvoja grupa, i u najmnanju ruku, kolokvij je bio neprimjeren (barem naša grupa)...
Ti ciklusi permutacija, taj dokaz ide prek cijele strane i više, užasno puno posla, zatim taj s 2 okrugla stola, 12 345 ljudi, i 2 uvjeta i zadnji koji je nerješiv u pola sata, sat za ljude inteligencije<150 čine kolokvij teškim:((((
_________________
Meni mama neda da.... Pričam sa dječacima... meni mama neda to-A što?-Jer kaže da je opasno!
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
ft
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (21:38:47)
Postovi: (25)16
|
 Postano: 22:54 sri, 28. 11. 2007 Naslov: Postano: 22:54 sri, 28. 11. 2007 Naslov: |
    |
|
|
[quote="Nori"]Ja se slažem s ft-om. Bila sam tvoja grupa, i u najmnanju ruku, kolokvij je bio neprimjeren (barem naša grupa)...
Ti ciklusi permutacija, taj dokaz ide prek cijele strane i više, užasno puno posla, zatim taj s 2 okrugla stola, 12 345 ljudi, i 2 uvjeta i zadnji koji je nerješiv u pola sata, sat za ljude inteligencije<150 čine kolokvij teškim:(((([/quote]
To je ono sta ja govorin. Nama drugi definitivno nije smija doci, ne zato sta je tezak jer nije, nego zato sta je demotivirajuci za daljne rijesavanje
| Nori (napisa): | Ja se slažem s ft-om. Bila sam tvoja grupa, i u najmnanju ruku, kolokvij je bio neprimjeren (barem naša grupa)...
Ti ciklusi permutacija, taj dokaz ide prek cijele strane i više, užasno puno posla, zatim taj s 2 okrugla stola, 12 345 ljudi, i 2 uvjeta i zadnji koji je nerješiv u pola sata, sat za ljude inteligencije<150 čine kolokvij teškim:(((( |
To je ono sta ja govorin. Nama drugi definitivno nije smija doci, ne zato sta je tezak jer nije, nego zato sta je demotivirajuci za daljne rijesavanje
|
|
| [Vrh] |
|
|














