| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kištra
Forumaš(ica)


Pridružen/a: 06. 03. 2008. (18:44:16)
Postovi: (3)16
Spol: 
Lokacija: Garesnica
|
|
| [Vrh] |
|
kištra
Forumaš(ica)


Pridružen/a: 06. 03. 2008. (18:44:16)
Postovi: (3)16
Spol: 
Lokacija: Garesnica
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 17:00 uto, 11. 3. 2008 Naslov: Postano: 17:00 uto, 11. 3. 2008 Naslov: |
    |
|
|
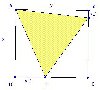
formule koje ti trebaju su sinus i kosinus iz pravokutnog trokuta, sinus i kosinus razlike kuteva, i povrsina pravokutnog trokuta ;)
na slici je uistinu pravokutnik, samo sto podsjeca na kvadrat da to nije normalno ;) (duljine stranica se razlikuju za jako malo)
predlazem da gledas sliku i sam si rijesis, ove formule vjerujem da u 4tom razredu srednje zbilja znas :)
[latex]
\alpha &= \measuredangle BAE \\
x_1 &= a \sin \alpha \\
y &= a \cos \alpha \\
y_1 &= a \sin \left( \frac{\pi}{6} - \alpha \right) \\
&= a \left( \frac{1}{2} \cos \alpha - \frac{\sqrt{3}}{2} \sin \alpha \right) \\
x &= a \cos \left( \frac{\pi}{6} - \alpha \right) \\
&= a \left( \frac{\sqrt{3}}{2} \cos \alpha + \frac{1}{2} \sin \alpha \right) \\
[/latex]
zelimo vidjeti jednakost povrsina, tj:
[latex]L := \frac{(x-x_1)(y-y_1)}{2} &\stackrel{?}{=} \frac{x_1y}{2} + \frac{xy_1}{2} =: D\\[/latex]
gledamo jednu stranu
[latex]2L &= (x-x_1)(y-y_1) \\
&= a \left( \frac{\sqrt{3}}{2} \cos \alpha + \frac{1}{2} \sin \alpha - \sin \alpha \right) a \left( \cos \alpha - \frac{1}{2} \cos \alpha + \frac{\sqrt{3}}{2} \sin \alpha \right) \\
&= a^2 \left(\frac{\sqrt{3}}{2} \cos \alpha - \frac{1}{2} \sin \alpha \right) \left(\frac{1}{2} \cos \alpha + \frac{\sqrt{3}}{2} \sin \alpha \right) \\
&= \cdots \\
&= a^2 \left( \frac{\sqrt{3}}{2} ({\cos}^2 \alpha - {\sin}^2 \alpha) + \frac{1}{2} \cos \alpha \sin \alpha \right)[/latex]
pa drugu
[latex]
2D &= x_1y + xy_1 \\
&= a \sin \alpha \ a \cos \alpha + a \left( \frac{1}{2} \cos \alpha - \frac{\sqrt{3}}{2} \sin \alpha \right) a \left( \frac{\sqrt{3}}{2} \cos \alpha + \frac{1}{2} \sin \alpha \right) \\
&= \cdots \\
&= a^2 \left( \frac{\sqrt{3}}{2} ({\cos}^2 \alpha - {\sin}^2 \alpha) + \frac{1}{2} \cos \alpha \sin \alpha \right)[/latex]
:weee: jednako je :weee:
umjesto ovih tockica slijedi mnozenje zagrada i minijaturno grupiranje da se dobije zavrsni zapis ;)
formule koje ti trebaju su sinus i kosinus iz pravokutnog trokuta, sinus i kosinus razlike kuteva, i povrsina pravokutnog trokuta 
na slici je uistinu pravokutnik, samo sto podsjeca na kvadrat da to nije normalno  (duljine stranica se razlikuju za jako malo) (duljine stranica se razlikuju za jako malo)
predlazem da gledas sliku i sam si rijesis, ove formule vjerujem da u 4tom razredu srednje zbilja znas 
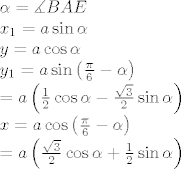
zelimo vidjeti jednakost povrsina, tj:
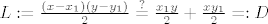
gledamo jednu stranu
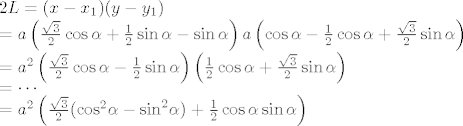
pa drugu
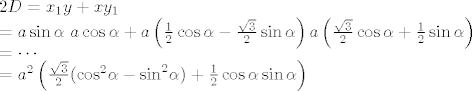
 jednako je jednako je 
umjesto ovih tockica slijedi mnozenje zagrada i minijaturno grupiranje da se dobije zavrsni zapis 
| Description: |
|
| Filesize: |
20.21 KB |
| Viewed: |
211 Time(s) |
|
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kištra
Forumaš(ica)


Pridružen/a: 06. 03. 2008. (18:44:16)
Postovi: (3)16
Spol: 
Lokacija: Garesnica
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 7:17 sri, 12. 3. 2008 Naslov: Postano: 7:17 sri, 12. 3. 2008 Naslov: |
    |
|
|
...ali se može "spasiti", da se ipak riješi samo uz pomoć Pitagore i formula za površinu pravokutnika i kvadrata.
Dakle, neka je AB = a, BC = b, BE = x, CF = y.
Trebalo bi pokazati da je
(b-x)y = ax + b(a-y).
Odmah da najavim - pokazat će se da je
x = 2b - a sqrt(3),
y = b sqrt(3) - a
pa je onda lako provjeriti jednakost, s obje strane bit će
4ab - (a^2 + b^2)sqrt(3).
Iz pravokutnih trokuta imamo
a^2 + x^2 = (b-x)^2 + y^2 = b^2+(a-y)^2.
Odavde se lako izvuče: 2ay = a^2 - x^2 + 2bx
pa možemo izraziti y.
Dalje, površina pravokutnika jednaka je ab i to je jednako zbroju 3 pravokutna trokuta i jednakostraničnog trokuta sa stranicom c, za koju vrijedi
c^2 = a^2 + x^2. površina tog trokuta je c^2 sqrt(3)/4.
Kad se to izjednači i sredi, pa se uvrsti y kako je izražen otprije, dobiva se jednadžba po x koja je 3. stupnja, ali se lako faktorizira. Ukratko, dobije se
(a^2 + x^2) (x + a sqrt(3) - 2b) = 0.
Kako je prvi faktor pozitivan, drugi mora biti 0 i zato x = 2b - a sqrt(3),
što je i najavljeno, a ostalo je lako.
Simpatičan zadatak, u biti prolazi i u 7. razredu osnovne škole...
...ali se može "spasiti", da se ipak riješi samo uz pomoć Pitagore i formula za površinu pravokutnika i kvadrata.
Dakle, neka je AB = a, BC = b, BE = x, CF = y.
Trebalo bi pokazati da je
(b-x)y = ax + b(a-y).
Odmah da najavim - pokazat će se da je
x = 2b - a sqrt(3),
y = b sqrt(3) - a
pa je onda lako provjeriti jednakost, s obje strane bit će
4ab - (a^2 + b^2)sqrt(3).
Iz pravokutnih trokuta imamo
a^2 + x^2 = (b-x)^2 + y^2 = b^2+(a-y)^2.
Odavde se lako izvuče: 2ay = a^2 - x^2 + 2bx
pa možemo izraziti y.
Dalje, površina pravokutnika jednaka je ab i to je jednako zbroju 3 pravokutna trokuta i jednakostraničnog trokuta sa stranicom c, za koju vrijedi
c^2 = a^2 + x^2. površina tog trokuta je c^2 sqrt(3)/4.
Kad se to izjednači i sredi, pa se uvrsti y kako je izražen otprije, dobiva se jednadžba po x koja je 3. stupnja, ali se lako faktorizira. Ukratko, dobije se
(a^2 + x^2) (x + a sqrt(3) - 2b) = 0.
Kako je prvi faktor pozitivan, drugi mora biti 0 i zato x = 2b - a sqrt(3),
što je i najavljeno, a ostalo je lako.
Simpatičan zadatak, u biti prolazi i u 7. razredu osnovne škole...
|
|
| [Vrh] |
|
|







