| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
ivo34
Forumaš(ica)


Pridružen/a: 03. 02. 2005. (10:11:04)
Postovi: (171)16
Spol: 
|
 Postano: 23:25 sub, 15. 3. 2008 Naslov: Postano: 23:25 sub, 15. 3. 2008 Naslov: |
    |
|
|
Sferne: x = r*cos(fi)*sin(psi), y = r*sin(fi)*sin(psi), z = r*cos(psi);
Kartezijeve: r = korijen(x^2+y^2) + z^2, tg(fi) = y/x, cos(psi) = z/y.
Ovo malo ruzno izgleda, ali je tocno (nadam se :wink: ).
Sferne: x = r*cos(fi)*sin(psi), y = r*sin(fi)*sin(psi), z = r*cos(psi);
Kartezijeve: r = korijen(x^2+y^2) + z^2, tg(fi) = y/x, cos(psi) = z/y.
Ovo malo ruzno izgleda, ali je tocno (nadam se  ). ).
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 0:08 ned, 16. 3. 2008 Naslov: Re: pitanje iz vjezbi Postano: 0:08 ned, 16. 3. 2008 Naslov: Re: pitanje iz vjezbi |
    |
|
|
[quote="kika"]Moze li mi netko tko je bio na prvim vjezbi iz Integrala kod asistentice Petre napisati iz zadnjeg primjera prije Parametarski zadane plohe i krivulje, koje su sferne koordinate, a koje su dobivene Kartezijeve koordinate?[/quote]
Sferne ( 2, pi/4, pi/3) -> kartezijeve ( sqrt(6)/2, sqrt(6)/2, 1)
Ak ti to treba ;)
| kika (napisa): | | Moze li mi netko tko je bio na prvim vjezbi iz Integrala kod asistentice Petre napisati iz zadnjeg primjera prije Parametarski zadane plohe i krivulje, koje su sferne koordinate, a koje su dobivene Kartezijeve koordinate? |
Sferne ( 2, pi/4, pi/3) → kartezijeve ( sqrt(6)/2, sqrt(6)/2, 1)
Ak ti to treba 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 10:13 sri, 2. 4. 2008 Naslov: Postano: 10:13 sri, 2. 4. 2008 Naslov: |
    |
|
|
Pitanje.
N nekim vježbama (zadnjim, predzadnjim, ne znam) je bila ona fja definirana na trokutu omeđenog sa (0,0),(1,1) i (1,-1) i glasi korjen(x^2-y^2).
Sad je to asistentica Tadić rješavala na neki čudan način (kužim supstituciju y=xsint) i dobila pi/6. Nije bilo računanja granica kod te supstitucije ni ičeg sličnog, pojavio se neki arcsin itd...
Rješio sam to na 'normalan' način (računanje granica, postanu -pi/2 i pi/2, pa 2x parcijalno) i dobio pi/4.
Mathematica kaže pi/6 pa pitam: di sam fulo?
Pitanje.
N nekim vježbama (zadnjim, predzadnjim, ne znam) je bila ona fja definirana na trokutu omeđenog sa (0,0),(1,1) i (1,-1) i glasi korjen(x^2-y^2).
Sad je to asistentica Tadić rješavala na neki čudan način (kužim supstituciju y=xsint) i dobila pi/6. Nije bilo računanja granica kod te supstitucije ni ičeg sličnog, pojavio se neki arcsin itd...
Rješio sam to na 'normalan' način (računanje granica, postanu -pi/2 i pi/2, pa 2x parcijalno) i dobio pi/4.
Mathematica kaže pi/6 pa pitam: di sam fulo?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
 Postano: 10:31 sri, 2. 4. 2008 Naslov: Postano: 10:31 sri, 2. 4. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Pitanje.
N nekim vježbama (zadnjim, predzadnjim, ne znam) je bila ona fja definirana na trokutu omeđenog sa (0,0),(1,1) i (1,-1) i glasi korjen(x^2-y^2).
Sad je to asistentica Tadić rješavala na neki čudan način (kužim supstituciju y=xsint) i dobila pi/6. Nije bilo računanja granica kod te supstitucije ni ičeg sličnog, pojavio se neki arcsin itd...
Rješio sam to na 'normalan' način (računanje granica, postanu -pi/2 i pi/2, pa 2x parcijalno) i dobio pi/4.
Mathematica kaže pi/6 pa pitam: di sam fulo?[/quote]
pa nije bilo potrebe za uvrstavanjem granica kad je ona tu supstituciju uvodila u neodredenom integralu,tj.vjerojatno je htjela da vidimo da je to opcenito za takav oblik integrala i da nema veze sa granicama.
isto bi ti bilo kao da si uzeo neki gotov integral iz tablice i onda isao uvrstit granice,nisi ih mijenjao i nije te bilo briga(bar mene :D ) kak je dobiven taj integral...
probaj si zamisliti da je to petra prepisala iz bronstajna-zavrsni rezultat,i onda isla racunati s granicama.
(a arcsin se pojavio jer joj je trebalo koliko je t da vrati supstituciju u neodredenom integralu :) )
| Luuka (napisa): | Pitanje.
N nekim vježbama (zadnjim, predzadnjim, ne znam) je bila ona fja definirana na trokutu omeđenog sa (0,0),(1,1) i (1,-1) i glasi korjen(x^2-y^2).
Sad je to asistentica Tadić rješavala na neki čudan način (kužim supstituciju y=xsint) i dobila pi/6. Nije bilo računanja granica kod te supstitucije ni ičeg sličnog, pojavio se neki arcsin itd...
Rješio sam to na 'normalan' način (računanje granica, postanu -pi/2 i pi/2, pa 2x parcijalno) i dobio pi/4.
Mathematica kaže pi/6 pa pitam: di sam fulo? |
pa nije bilo potrebe za uvrstavanjem granica kad je ona tu supstituciju uvodila u neodredenom integralu,tj.vjerojatno je htjela da vidimo da je to opcenito za takav oblik integrala i da nema veze sa granicama.
isto bi ti bilo kao da si uzeo neki gotov integral iz tablice i onda isao uvrstit granice,nisi ih mijenjao i nije te bilo briga(bar mene  ) kak je dobiven taj integral... ) kak je dobiven taj integral...
probaj si zamisliti da je to petra prepisala iz bronstajna-zavrsni rezultat,i onda isla racunati s granicama.
(a arcsin se pojavio jer joj je trebalo koliko je t da vrati supstituciju u neodredenom integralu  ) )
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 11:06 sri, 16. 4. 2008 Naslov: Postano: 11:06 sri, 16. 4. 2008 Naslov: |
    |
|
|
Opet ja. :)
Baš mi nije sjela ova zamjena varijabli pa ako ima neka dobra duša da to malo pojasni... Uglavnom želimo 'promijeniti' područje integracije da bi mogli napisati granice kod integrala ( ili? )... zadatak dan za dz je :
[latex]\int_{B}{(x^2-y^2)dxdy}[/latex]
gdje je B paralelogram omeđen sa (1,1), (2,2), (0,0), (4/3 , 10/3).
Mi sad taj paralelogram želimo pretvoriti u nešto lijepo (kvadrat?) da bi znali granice za x i y. zamjena bi bila u=x-y, v=x+y , pa je
fi(u,v) = (x,y) tj. fi^-1 (x,y)=(x-y,x+y) Sad izračunamo jakobian of fi^-1, nađemo jakobian od fi preko binet-cauchy i kaj sad? Kak nać što je A=fi(B) ?
edit: Probah kak smo radili na vježbama, promatrat one pravce pa u ovisnosti x,y vidjet kak se ponašaju u,v. Dobih 4 pravokutnika (u u-v sustavu) i sad samo integriram po tih 4 pravokutnika fju uv (koja ispadne od (x-y)(x+y) )?
Opet ja. 
Baš mi nije sjela ova zamjena varijabli pa ako ima neka dobra duša da to malo pojasni... Uglavnom želimo 'promijeniti' područje integracije da bi mogli napisati granice kod integrala ( ili? )... zadatak dan za dz je :
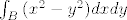
gdje je B paralelogram omeđen sa (1,1), (2,2), (0,0), (4/3 , 10/3).
Mi sad taj paralelogram želimo pretvoriti u nešto lijepo (kvadrat?) da bi znali granice za x i y. zamjena bi bila u=x-y, v=x+y , pa je
fi(u,v) = (x,y) tj. fi^-1 (x,y)=(x-y,x+y) Sad izračunamo jakobian of fi^-1, nađemo jakobian od fi preko binet-cauchy i kaj sad? Kak nać što je A=fi(B) ?
edit: Probah kak smo radili na vježbama, promatrat one pravce pa u ovisnosti x,y vidjet kak se ponašaju u,v. Dobih 4 pravokutnika (u u-v sustavu) i sad samo integriram po tih 4 pravokutnika fju uv (koja ispadne od (x-y)(x+y) )?
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
andreao
Forumaš(ica)


Pridružen/a: 10. 02. 2005. (12:08:18)
Postovi: (46F)16
Lokacija: SK
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
kika
Forumaš(ica)

Pridružen/a: 11. 02. 2005. (09:36:12)
Postovi: (188)16
|
 Postano: 23:08 čet, 17. 4. 2008 Naslov: Postano: 23:08 čet, 17. 4. 2008 Naslov: |
    |
|
|
[quote="Luuka"]
edit: Probah kak smo radili na vježbama, promatrat one pravce pa u ovisnosti x,y vidjet kak se ponašaju u,v. Dobih 4 pravokutnika (u u-v sustavu) i sad samo integriram po tih 4 pravokutnika fju uv (koja ispadne od (x-y)(x+y) )?[/quote]
jesi uspio sve skuziti?
ovaj integral kaj si napisao i koji ide po novom podrucju je u*v*|Jg(u,v)|dudv (u i v zbog (x-y)(x+y),a Jg(u,v) zbog teorema o zamjeni varijabli)
| Luuka (napisa): |
edit: Probah kak smo radili na vježbama, promatrat one pravce pa u ovisnosti x,y vidjet kak se ponašaju u,v. Dobih 4 pravokutnika (u u-v sustavu) i sad samo integriram po tih 4 pravokutnika fju uv (koja ispadne od (x-y)(x+y) )? |
jesi uspio sve skuziti?
ovaj integral kaj si napisao i koji ide po novom podrucju je u*v*|Jg(u,v)|dudv (u i v zbog (x-y)(x+y),a Jg(u,v) zbog teorema o zamjeni varijabli)
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 23:27 čet, 17. 4. 2008 Naslov: Postano: 23:27 čet, 17. 4. 2008 Naslov: |
    |
|
|
[quote="kika"]meni se cini da je taj crtez ona zamislila da je zadan,pa iz njega gledas kaj je kaj....
jos mi je i nacrtan prije rjesenja zadatka,bas kao da je tekst zadatka...
neka me netko ispravi ak grijesim :oops:[/quote]
pa naravno da je zadan. :? pa moraš znati područje po kojem integriraš. u zadatku piše da je to tetraedar s vrhovima (0,0,0), (0,0,1), (0,1,0) i (1,0,0). ne?
u principu ti je tu poredak integracije nebitan jer je stvar simetrična pa je svejedno otkud krećeš. recimo, izvana prema unutra neka ide x, y, z. tada ti x ide od 0 do 1, y ti ide od 0 do pravca u xy ravnini koji je rub stranice tog tetraedra, tj. do 1-x, a z ide od 0 do one ravnine (recimo baze tetraedra) koja prolazi točkama (0,0,1), (0,1,0) i (1,0,0), tj. z=-x-y+1, ako se ne varam.
nadam se da je jasnije :wink:
| kika (napisa): | meni se cini da je taj crtez ona zamislila da je zadan,pa iz njega gledas kaj je kaj....
jos mi je i nacrtan prije rjesenja zadatka,bas kao da je tekst zadatka...
neka me netko ispravi ak grijesim  |
pa naravno da je zadan.  pa moraš znati područje po kojem integriraš. u zadatku piše da je to tetraedar s vrhovima (0,0,0), (0,0,1), (0,1,0) i (1,0,0). ne? pa moraš znati područje po kojem integriraš. u zadatku piše da je to tetraedar s vrhovima (0,0,0), (0,0,1), (0,1,0) i (1,0,0). ne?
u principu ti je tu poredak integracije nebitan jer je stvar simetrična pa je svejedno otkud krećeš. recimo, izvana prema unutra neka ide x, y, z. tada ti x ide od 0 do 1, y ti ide od 0 do pravca u xy ravnini koji je rub stranice tog tetraedra, tj. do 1-x, a z ide od 0 do one ravnine (recimo baze tetraedra) koja prolazi točkama (0,0,1), (0,1,0) i (1,0,0), tj. z=-x-y+1, ako se ne varam.
nadam se da je jasnije 
_________________
ima let u finish
|
|
| [Vrh] |
|
|














