| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
frikmen2
Forumaš(ica)
Pridružen/a: 04. 11. 2006. (12:12:01)
Postovi: (2B)16
|
 Postano: 16:56 čet, 10. 4. 2008 Naslov: sup(AB)=supA*subB Postano: 16:56 čet, 10. 4. 2008 Naslov: sup(AB)=supA*subB |
    |
|
|
Zanima me rješenje (dokaz) zadatka 1.10 iz skripte prof. Guljaša (str.35) koji glasi:
Neka su A i B iz R+ odozgo ograničeni neprazni skupovi. Treba dokazati da je tada i AB={xy | x€A, y€B} odozgo ograničen i da vrijedi sup(AB)=supA*supB.
Ovo prvo u dokazu, to da je skup AB ograničen kužim. Našli smo broj (supA*supB) koji je veći od svakog elementa iz AB.
Ali ovo dalje gdje se dokazuje da je sup(AB)=supA*supB mi nije baš kristalno jasno. Tu se uzima epsilon veći od nule i manji od (supA+supB)/2. I na kraju se kaže "zbog proizvoljnosti od epsilon tvrdnja vrijedi...". Ali, po meni, tu epsilon nije proizvoljan, nego je iz intervala <0, (supA+supB)/2>.
Ovo za epsilon_0 mi je (valjda) jasno zašto je takav odabran. Zato da se nakon množenja dobije -epsilon i na kraju ispada da (supA+supB)/2-epsilon nije limes.
Nadam se da sam dovoljno dobro pojasnio u čemu je problem. Ponovit ću pitanje: ako je na početku epsilon < (supA+supB)/2 kako na kraju možemo reći da je epsilon proizvoljan.
Dokaz iz knjige je attachan.
Zanima me rješenje (dokaz) zadatka 1.10 iz skripte prof. Guljaša (str.35) koji glasi:
Neka su A i B iz R+ odozgo ograničeni neprazni skupovi. Treba dokazati da je tada i AB={xy | x€A, y€B} odozgo ograničen i da vrijedi sup(AB)=supA*supB.
Ovo prvo u dokazu, to da je skup AB ograničen kužim. Našli smo broj (supA*supB) koji je veći od svakog elementa iz AB.
Ali ovo dalje gdje se dokazuje da je sup(AB)=supA*supB mi nije baš kristalno jasno. Tu se uzima epsilon veći od nule i manji od (supA+supB)/2. I na kraju se kaže "zbog proizvoljnosti od epsilon tvrdnja vrijedi...". Ali, po meni, tu epsilon nije proizvoljan, nego je iz intervala <0, (supA+supB)/2>.
Ovo za epsilon_0 mi je (valjda) jasno zašto je takav odabran. Zato da se nakon množenja dobije -epsilon i na kraju ispada da (supA+supB)/2-epsilon nije limes.
Nadam se da sam dovoljno dobro pojasnio u čemu je problem. Ponovit ću pitanje: ako je na početku epsilon < (supA+supB)/2 kako na kraju možemo reći da je epsilon proizvoljan.
Dokaz iz knjige je attachan.
|
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
|
| [Vrh] |
|
frikmen2
Forumaš(ica)
Pridružen/a: 04. 11. 2006. (12:12:01)
Postovi: (2B)16
|
 Postano: 17:56 čet, 10. 4. 2008 Naslov: Postano: 17:56 čet, 10. 4. 2008 Naslov: |
    |
|
|
Po definiciji supremuma supA je najmanja gornja međa skupa A. Znači, za bilo koji epsilon veći od 0 broj supA-epsilon nije supremum, odnosno imat ćemo neki element iz A veći od supA-epsilon.
Mi tu želimo pokazati da je supA*supB supremum skupa AB, odnosno, ako se pomaknemo za [u]bilo koji[/u] epsilon veći od 0 u lijevo od supA*supB (koji je supremum skupa) da ćemo naići na neki element iz AB.
U dokazu je epsilon manji od (supA+supB)/2, što nije proizvoljan broj veći od nule.
Po definiciji supremuma supA je najmanja gornja međa skupa A. Znači, za bilo koji epsilon veći od 0 broj supA-epsilon nije supremum, odnosno imat ćemo neki element iz A veći od supA-epsilon.
Mi tu želimo pokazati da je supA*supB supremum skupa AB, odnosno, ako se pomaknemo za bilo koji epsilon veći od 0 u lijevo od supA*supB (koji je supremum skupa) da ćemo naići na neki element iz AB.
U dokazu je epsilon manji od (supA+supB)/2, što nije proizvoljan broj veći od nule.
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:56 čet, 10. 4. 2008 Naslov: Postano: 19:56 čet, 10. 4. 2008 Naslov: |
    |
|
|
[quote="frikmen2"]U dokazu je epsilon manji od (supA+supB)/2, što nije proizvoljan broj veći od nule.[/quote]
U tom dijelu dokaza bi se možda trebalo ubaciti "bez smanjenja općenitosti". Epsilon je tako odabran radi lakšeg naštimavanja. Ako uzmeš npr.
[latex]0<\varepsilon<\sup{A}+\sup{B}[/latex]
i analogno definiraš [latex]\varepsilon_0[/latex] te provedeš iste korake, i dalje će vrijediti
[latex]xy>\varepsilon_0^2-(\sup{A}+\sup{B})\varepsilon_0+\sup{A}\sup{B}[/latex],
samo što će ovaj put umjesto [latex]\varepsilon_0^2-(\sup{A}+\sup{B})\varepsilon_0 > - \varepsilon[/latex] vrijediti [latex]\varepsilon_0^2-2(\sup{A}+\sup{B})\varepsilon_0 > - \varepsilon[/latex]
pa neće odmah biti očito da je [latex]xy > \sup{A}\sup{B}-\varepsilon[/latex] (ali nakon malo raspisivanja i korištenja da su [latex]\varepsilon_0[/latex] i [latex](\sup{A}+\sup{B})[/latex] pozitivni pokaže se da je tako).
Slično možeš provesti dokaz i kada je [latex]0<\varepsilon<n(\sup{A}+\sup{B})[/latex], za svaki [latex]n \in \mathbb{N}[/latex]. A jasno je da koji god ti [latex]\varepsilon>0[/latex] odabrao, uvijek će postojati dovoljno velik [latex]n \in \mathbb{N}[/latex] takav da vrijedi [latex]0<\varepsilon<n(\sup{A}+\sup{B})[/latex]. Zato je [latex]\varepsilon>0[/latex] zbilja proizvoljan iako je malo šturo obrazloženo zašto.
| frikmen2 (napisa): | | U dokazu je epsilon manji od (supA+supB)/2, što nije proizvoljan broj veći od nule. |
U tom dijelu dokaza bi se možda trebalo ubaciti "bez smanjenja općenitosti". Epsilon je tako odabran radi lakšeg naštimavanja. Ako uzmeš npr.
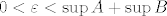
i analogno definiraš 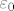 te provedeš iste korake, i dalje će vrijediti te provedeš iste korake, i dalje će vrijediti
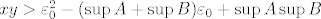 , ,
samo što će ovaj put umjesto 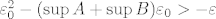 vrijediti vrijediti 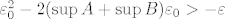
pa neće odmah biti očito da je 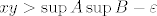 (ali nakon malo raspisivanja i korištenja da su (ali nakon malo raspisivanja i korištenja da su 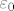 i i  pozitivni pokaže se da je tako). pozitivni pokaže se da je tako).
Slično možeš provesti dokaz i kada je 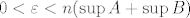 , za svaki , za svaki  . A jasno je da koji god ti . A jasno je da koji god ti 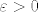 odabrao, uvijek će postojati dovoljno velik odabrao, uvijek će postojati dovoljno velik  takav da vrijedi takav da vrijedi 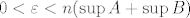 . Zato je . Zato je 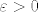 zbilja proizvoljan iako je malo šturo obrazloženo zašto. zbilja proizvoljan iako je malo šturo obrazloženo zašto.
_________________
The Dude Abides
|
|
| [Vrh] |
|
|







