| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 13:49 ned, 28. 9. 2008 Naslov: Postano: 13:49 ned, 28. 9. 2008 Naslov: |
    |
|
|
Neka [latex]Y\sim N(\mu,\sigma^2)[/latex], tada [latex]\mathbb{P}\{\frac{1}{Y}\leq 1\}=\mathbb{P}\{\omega\in \Omega: Y(\omega)\in (-\infty,0)\cup [1,\infty)\}[/latex], ostavljam ti da zavrsis. Inace "rubovi" doticnih skupova uopce nisu vazni, jer je fija gustoce of Y neprekidna. Mozes primjetiti, da se zadatak zapravo svodi na algebarsko manipuliranje, a ne na vjerojanost :( .
Neka 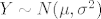 , tada , tada 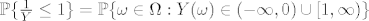 , ostavljam ti da zavrsis. Inace "rubovi" doticnih skupova uopce nisu vazni, jer je fija gustoce of Y neprekidna. Mozes primjetiti, da se zadatak zapravo svodi na algebarsko manipuliranje, a ne na vjerojanost , ostavljam ti da zavrsis. Inace "rubovi" doticnih skupova uopce nisu vazni, jer je fija gustoce of Y neprekidna. Mozes primjetiti, da se zadatak zapravo svodi na algebarsko manipuliranje, a ne na vjerojanost  . .
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 17:57 ned, 28. 9. 2008 Naslov: Postano: 17:57 ned, 28. 9. 2008 Naslov: |
    |
|
|
1. (a) Brutalni racun to rjesava ( koliko vidim nisi se ni potrudio rjesiti, jer ovo ide direktno iz definicije ).
(b) Ne.
2. Imas teorem koji kaze da ako su [latex]X_n[/latex] nenegativne sl. varijable ( cak izmjerive funkcije ), da tada [latex]\mathbb{E}[\sum_{n=1}^{\infty}X_n]=\sum_{n=1}^{\infty}\mathbb{E}[X_n][/latex], pa ostatak ostavljam tebi. Ne znam kako ces se za varijancu "jeftino" izvuci.
3. Ne znam, ovako na brzinu.
Edit: Uvjet u 3. zapravo znaci da je [latex]\mathbb{E}[X^2]=2[/latex]
1. (a) Brutalni racun to rjesava ( koliko vidim nisi se ni potrudio rjesiti, jer ovo ide direktno iz definicije ).
(b) Ne.
2. Imas teorem koji kaze da ako su 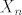 nenegativne sl. varijable ( cak izmjerive funkcije ), da tada nenegativne sl. varijable ( cak izmjerive funkcije ), da tada 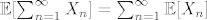 , pa ostatak ostavljam tebi. Ne znam kako ces se za varijancu "jeftino" izvuci. , pa ostatak ostavljam tebi. Ne znam kako ces se za varijancu "jeftino" izvuci.
3. Ne znam, ovako na brzinu.
Edit: Uvjet u 3. zapravo znaci da je 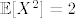
Zadnja promjena: Mr.Doe; 8:56 pon, 29. 9. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
 Postano: 10:12 pon, 29. 9. 2008 Naslov: Postano: 10:12 pon, 29. 9. 2008 Naslov: |
    |
|
|
[quote="Mr.Doe"]1. (a) Brutalni racun to rjesava ( koliko vidim nisi se ni potrudio rjesiti, jer ovo ide direktno iz definicije ).
[/quote]
potrudio se jesam. al mi nije bilo smisla navodit pokušaj koji se nije maknuo od početka...nevidim kako to izračunati, slabo mi idu ta očekivanja i varijance..evo moj pokušaj:
[latex]Cov (X+Y,|X-Y|)=E((X+Y-EX-EY)(|X-Y|-E|X-Y|)[/latex]
i sad već više neznam kaj bi dalje. kako izračunati E|X-Y| ?
znam da je [latex]EX=EY=\frac{1}{2}[/latex] i [latex]Var X=Var Y=\frac{1}{4}[/latex] ali mi baš i ne pomaže puno. :cry:
[quote]
(b) Ne.
[/quote]
mislim da sam uspio sad dobiti da nisu. ovak:
[latex]P(X+Y=1, |X-Y|=1)=P(X=1,Y=0)+P(X=0,Y=1)=2npq^{2n-1} \ [/latex] [b](1)[/b]
[latex]P(X+Y=1)*P(|X-Y|=1)=(npq^{2n-1})^2 \ [/latex] [b](2)[/b]
i sad [b](1)[/b]!=[b](2) [/b] => nisu nezavisni.
to dobro?
[quote="Mr.Doe"]
2. Imas teorem koji kaze da ako su [latex]X_n[/latex] nenegativne sl. varijable ( cak izmjerive funkcije ), da tada [latex]\mathbb{E}[\sum_{n=1}^{\infty}X_n]=\sum_{n=1}^{\infty}\mathbb{E}[X_n][/latex], pa ostatak ostavljam tebi. [/quote]
hmm...ne znam za taj teorem. mislim da ga nema u predavanjima prof.Sarape.
znam da ima onaj da je za nezavisne sl.var. [latex]\mathbb{E}[\Pi_{k=1}^{n}X_k]=\Pi_{k=1}^{n}\mathbb{E}[X_k][/latex] al ovaj nisam vidio. :shock:
| Mr.Doe (napisa): | 1. (a) Brutalni racun to rjesava ( koliko vidim nisi se ni potrudio rjesiti, jer ovo ide direktno iz definicije ).
|
potrudio se jesam. al mi nije bilo smisla navodit pokušaj koji se nije maknuo od početka...nevidim kako to izračunati, slabo mi idu ta očekivanja i varijance..evo moj pokušaj:

i sad već više neznam kaj bi dalje. kako izračunati E|X-Y| ?
znam da je 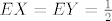 i i 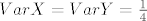 ali mi baš i ne pomaže puno. ali mi baš i ne pomaže puno. 
mislim da sam uspio sad dobiti da nisu. ovak:
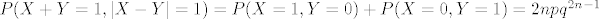 (1) (1)
 (2) (2)
i sad (1)!=(2) ⇒ nisu nezavisni.
to dobro?
| Mr.Doe (napisa): |
2. Imas teorem koji kaze da ako su 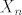 nenegativne sl. varijable ( cak izmjerive funkcije ), da tada nenegativne sl. varijable ( cak izmjerive funkcije ), da tada 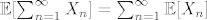 , pa ostatak ostavljam tebi. , pa ostatak ostavljam tebi. |
hmm...ne znam za taj teorem. mislim da ga nema u predavanjima prof.Sarape.
znam da ima onaj da je za nezavisne sl.var. 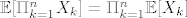 al ovaj nisam vidio. al ovaj nisam vidio. 
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
 Postano: 13:15 pon, 29. 9. 2008 Naslov: Postano: 13:15 pon, 29. 9. 2008 Naslov: |
    |
|
|
evo, tu su rjesena par rokova koja sam ja rijesio, ajde ih prekontrolirajte, posebno me zanima 22.04.2008 rok, 2. zadatak, ak moze mala pomoc.
hvala!
evo, tu su rjesena par rokova koja sam ja rijesio, ajde ih prekontrolirajte, posebno me zanima 22.04.2008 rok, 2. zadatak, ak moze mala pomoc.
hvala!
_________________  Everything happens with a reason! 

| Description: |
|

Download |
| Filename: |
uvis rjeseni 27062008.pdf |
| Filesize: |
255.82 KB |
| Downloaded: |
286 Time(s) |
| Description: |
|

Download |
| Filename: |
uvis rjeseni 22042008.pdf |
| Filesize: |
275.67 KB |
| Downloaded: |
304 Time(s) |
| Description: |
|

Download |
| Filename: |
uvis rjeseni 11072008.pdf |
| Filesize: |
198.9 KB |
| Downloaded: |
264 Time(s) |
|
|
| [Vrh] |
|
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
 Postano: 18:44 pon, 29. 9. 2008 Naslov: Postano: 18:44 pon, 29. 9. 2008 Naslov: |
    |
|
|
a jesam bedast ne vidim najjednostavnije rješenje :oops: uvijek mislim da mora biti nešto komplicirano....
@filipnet:
po ovom što si ti napisao u tom 2.zadatku ide dalje
(X+Y)*|X-Y|=[0 (5/8 ), 1 (1/4), 2 (1/8 ) ]
(ovo bez zag.su vrijednosti, a u okruglim zagradama su vjerojatnosti)
to se dobije iz ovih tvojih razdioba od (X+Y) i |X-Y|
npr. za 0 gledaš koje sve kombinacije mogu za umnožak dati 0 => 0-0, 0-1, 1-0, 2-0 [b]([/b][i]vrijednost (X+Y)[/i][b]-[/b][i]vrijednost|X-Y[/i]|[b]) [/b]=> vjerojatnost je 1/4*1/2+1/4*1/2+1/2*1/2+1/4*1/2=5/8
dakle množiš vjer.iz jedne i druge razdiobe za 0-0 + umnož.vjer. za 0-1 + umnož.za 1-0 + umnož.za 2-0.
bar mislim da je tako.
[quote="Mr.Doe"]
Edit: Uvjet u 3. zapravo znaci da je [latex]\mathbb{E}[X^2]=2[/latex][/quote]
kak se dobije to?
a jesam bedast ne vidim najjednostavnije rješenje  uvijek mislim da mora biti nešto komplicirano.... uvijek mislim da mora biti nešto komplicirano....
@filipnet:
po ovom što si ti napisao u tom 2.zadatku ide dalje
(X+Y)*|X-Y|=[0 (5/8 ), 1 (1/4), 2 (1/8 ) ]
(ovo bez zag.su vrijednosti, a u okruglim zagradama su vjerojatnosti)
to se dobije iz ovih tvojih razdioba od (X+Y) i |X-Y|
npr. za 0 gledaš koje sve kombinacije mogu za umnožak dati 0 ⇒ 0-0, 0-1, 1-0, 2-0 (vrijednost (X+Y)-vrijednost|X-Y|) ⇒ vjerojatnost je 1/4*1/2+1/4*1/2+1/2*1/2+1/4*1/2=5/8
dakle množiš vjer.iz jedne i druge razdiobe za 0-0 + umnož.vjer. za 0-1 + umnož.za 1-0 + umnož.za 2-0.
bar mislim da je tako.
| Mr.Doe (napisa): |
Edit: Uvjet u 3. zapravo znaci da je 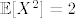 |
kak se dobije to?
|
|
| [Vrh] |
|
|








