| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:16 ned, 26. 10. 2008 Naslov: Postano: 22:16 ned, 26. 10. 2008 Naslov: |
    |
|
|
A kaj ti treba objasnit? Jer pitanje je prilično neodređeno... nije ti jasna primjena, dokazi tvrdnji, što ti kriteriji predstavljaju?
Imaš tu popis kriterija, i mislim pokoji primjer, možda ti to riješi koje pitanje: [url]http://degiorgi.math.hr/forum/viewtopic.php?t=10335[/url]
A kaj ti treba objasnit? Jer pitanje je prilično neodređeno... nije ti jasna primjena, dokazi tvrdnji, što ti kriteriji predstavljaju?
Imaš tu popis kriterija, i mislim pokoji primjer, možda ti to riješi koje pitanje: http://degiorgi.math.hr/forum/viewtopic.php?t=10335
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
AnAA
Forumaš(ica)

Pridružen/a: 25. 10. 2008. (16:00:57)
Postovi: (12)16
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 13:31 sub, 1. 11. 2008 Naslov: Postano: 13:31 sub, 1. 11. 2008 Naslov: |
    |
|
|
Dakle ovako za Leibnitza, on kaže:
an padajući nakon nekog indexa, an>0, lim(an)=0 onda red [latex]\sum{(-1)^{n}a_{n}} [/latex] konvergira.
Pa trebaš provjerit dal je tvoj niz padajuć i ima li poz članove (ne gledaš onaj (-1)^n ) i to je to... Leibnitz daje da konv...
Tvoj niz očito ima poz članove ( i arctgn i korijen(n) su pozitivni ), treba još provjerit dal je padajuć... a i to je istina jer arctg(n) raste, a 1/korijen(n) pada pa sveukupno pada
-> red konvergira.
:D :D :D :D
Dakle ovako za Leibnitza, on kaže:
an padajući nakon nekog indexa, an>0, lim(an)=0 onda red 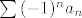 konvergira. konvergira.
Pa trebaš provjerit dal je tvoj niz padajuć i ima li poz članove (ne gledaš onaj (-1)^n ) i to je to... Leibnitz daje da konv...
Tvoj niz očito ima poz članove ( i arctgn i korijen(n) su pozitivni ), treba još provjerit dal je padajuć... a i to je istina jer arctg(n) raste, a 1/korijen(n) pada pa sveukupno pada
→ red konvergira.
   
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:54 ned, 16. 11. 2008 Naslov: Postano: 16:54 ned, 16. 11. 2008 Naslov: |
    |
|
|
Prozuji malo po forumu, ima toga dosta... a ugl je slično, uzmeš red koji je za fju slično tvojoj i onda deriviraš, integriraš, ovisi kaj trebaš... pitaj konkretno...
Prozuji malo po forumu, ima toga dosta... a ugl je slično, uzmeš red koji je za fju slično tvojoj i onda deriviraš, integriraš, ovisi kaj trebaš... pitaj konkretno...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|








