| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
hrcho
Forumaš(ica)

Pridružen/a: 21. 10. 2007. (17:54:17)
Postovi: (7)16
Lokacija: tko zna neka mi kaze
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
hrcho
Forumaš(ica)

Pridružen/a: 21. 10. 2007. (17:54:17)
Postovi: (7)16
Lokacija: tko zna neka mi kaze
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
hrcho
Forumaš(ica)

Pridružen/a: 21. 10. 2007. (17:54:17)
Postovi: (7)16
Lokacija: tko zna neka mi kaze
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:50 uto, 18. 11. 2008 Naslov: Postano: 0:50 uto, 18. 11. 2008 Naslov: |
    |
|
|
[quote="hrcho"]1. Neka je M zbroj prvih 2006^2006 prostih brojeva. Odredi ostatak pri dijeljenju M^2 s 8.[/quote]
[latex]M[/latex] je suma [latex]2006^{2006}[/latex] prostih brojeva, [latex]2006^{2006}[/latex] je paran broj, pa se u sumi pojavljuje neparno mnogo neparnih brojeva (točnije, njih [latex]2006^{2006}-1[/latex]), te jedan paran broj, jedini paran prost broj je broj [latex]2[/latex]. Dakle, [latex]M[/latex] je neparan broj. Kvadrat bilo kojeg neparnog cijelog broja daje ostatak [latex]1[/latex] pri dijeljenju s [latex]8[/latex], dakle [latex]M^2 \equiv 1 \pmod{8}[/latex].
Ova činjenica se lako pokaže, naime, neka je [latex]n[/latex] neparan cijeli broj, tada postoji cijeli broj [latex]k[/latex] takav da je [latex]n = 2k -1[/latex]. Sada nam je [latex]n^2 = 4k^2 -4k +1 = 4k\left(k-1\right)+1[/latex]. Broj [latex]k\left(k-1\right)[/latex] je paran jer je umnožak dva uzastopna cijela broja.
| hrcho (napisa): | | 1. Neka je M zbroj prvih 2006^2006 prostih brojeva. Odredi ostatak pri dijeljenju M^2 s 8. |
 je suma je suma 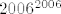 prostih brojeva, prostih brojeva, 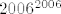 je paran broj, pa se u sumi pojavljuje neparno mnogo neparnih brojeva (točnije, njih je paran broj, pa se u sumi pojavljuje neparno mnogo neparnih brojeva (točnije, njih 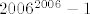 ), te jedan paran broj, jedini paran prost broj je broj ), te jedan paran broj, jedini paran prost broj je broj  . Dakle, . Dakle,  je neparan broj. Kvadrat bilo kojeg neparnog cijelog broja daje ostatak je neparan broj. Kvadrat bilo kojeg neparnog cijelog broja daje ostatak  pri dijeljenju s pri dijeljenju s 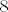 , dakle , dakle 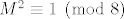 . .
Ova činjenica se lako pokaže, naime, neka je  neparan cijeli broj, tada postoji cijeli broj neparan cijeli broj, tada postoji cijeli broj  takav da je takav da je 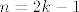 . Sada nam je . Sada nam je 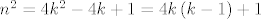 . Broj . Broj 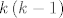 je paran jer je umnožak dva uzastopna cijela broja. je paran jer je umnožak dva uzastopna cijela broja.
|
|
| [Vrh] |
|
|








