imam problem sa shvacanjem ovog teorema, vjerojatno je neka glupa greska ali ja fakat jednu stvar ne razumijem.
dakle, Liouvilleov teorem kaze sljedece:
Svaka holomorfna funkcija, za koju postoji [latex]M \in \mathbb{N}[/latex] takav da vrijedi [latex]\lvert f(z) \rvert \leq M \quad \forall z \in \mathbb{C}[/latex], je konstantna.
dokaz teorema:
dokaz koristi cinjenicu da je svaka holomorfna funkcija analiticka. buduci da je f cijela funkcija, mozemo je razviti u Taylorov red (oko 0):
[latex]f(z)=\sum\limits_{k=0}^{+\infty} a_k z^k[/latex]
gdje je [latex]a_k[/latex] (preko Cauchyeve integralne formule) jednak
[latex]a_k=\frac{f^{(k)}(0)}{k!}=\frac{1}{2\pi i}\oint\limits_ {C_r} \frac{f(\zeta)}{\zeta^{k+1}}\text{d}\zeta[/latex]
[latex]C_r[/latex] je kruznica radijusa r oko ishodista i r>0. sada mozemo direktno procijeniti:
[latex]\lvert a_k \rvert \leq \frac{1}{2\pi i}\oint\limits_ {C_r} \frac{\lvert f(\zeta) \rvert}{\lvert \zeta\rvert^{k+1}}\text{d}\zeta \leq \frac{1}{2\pi} \oint\limits_ {C_r} \frac{M}{r^{k+1}}}\text{d}\zeta=\frac{M}{2\pi r^{k+1}}\oint\limits_{C_r}\text{d}\zeta=\frac{M}{2\pi r^{k+1}}2\pi r=\frac{M}{r^k}[/latex]
gdje smo u drugoj nejedakosti koristili pretpostavku da je [latex]f(z)\leq M \quad \forall z\in \mathbb{C}[/latex] te cinjenicu da je [latex] \lvert z \rvert = r[/latex] na kruznici [latex]C_r[/latex]. izbor za r je potpuno proizvoljan. stoga, ako r pustamo u beskonacnost, dolazimo do toga da je [latex]a_k=0 \quad \forall k \geq 1[/latex]. iz toga slijedi da je f(z) konstantna funkcija, odnosno [latex]f(z)=a_k[/latex].
ok, sad slijedi pitanje. ovaj sredisnji dio je u biti maksimum funkcije na kruznici C_r. pretpostavka teorema je da je funkcija omedjena s gornje strane sa nekakvim M, sto znaci da je maksimum funkcije uvijek manji od tog M. i sad, koliko god mi povecavali ili smanjivali r (od 0 do beskonacno), sredisnji dio ce uvijek biti strogo manji od onog dijela desno jer je maksimum funkcije uvijek strogo manji od M. da li je ovo dovoljno dobar opis ovoga sto se gore desava? i jos nesto, zasto pustamo [latex]r\to +\infty[/latex]?
imam problem sa shvacanjem ovog teorema, vjerojatno je neka glupa greska ali ja fakat jednu stvar ne razumijem.
dakle, Liouvilleov teorem kaze sljedece:
Svaka holomorfna funkcija, za koju postoji 
takav da vrijedi 
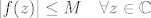, je konstantna.
dokaz teorema:
dokaz koristi cinjenicu da je svaka holomorfna funkcija analiticka. buduci da je f cijela funkcija, mozemo je razviti u Taylorov red (oko 0):
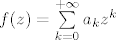
gdje je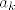 
(preko Cauchyeve integralne formule) jednak
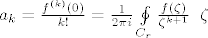
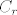je kruznica radijusa r oko ishodista i r>0. sada mozemo direktno procijeniti:
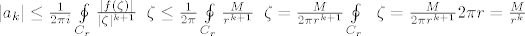
gdje smo u drugoj nejedakosti koristili pretpostavku da je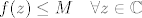 
te cinjenicu da je 
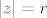na kruznici 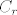. izbor za r je potpuno proizvoljan. stoga, ako r pustamo u beskonacnost, dolazimo do toga da je 
. iz toga slijedi da je f(z) konstantna funkcija, odnosno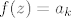 
.
ok, sad slijedi pitanje. ovaj sredisnji dio je u biti maksimum funkcije na kruznici C_r. pretpostavka teorema je da je funkcija omedjena s gornje strane sa nekakvim M, sto znaci da je maksimum funkcije uvijek manji od tog M. i sad, koliko god mi povecavali ili smanjivali r (od 0 do beskonacno), sredisnji dio ce uvijek biti strogo manji od onog dijela desno jer je maksimum funkcije uvijek strogo manji od M. da li je ovo dovoljno dobar opis ovoga sto se gore desava? i jos nesto, zasto pustamo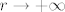 
?
