| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 23:55 uto, 3. 2. 2009 Naslov: Re: 6. domaća zadaća Postano: 23:55 uto, 3. 2. 2009 Naslov: Re: 6. domaća zadaća |
    |
|
|
[quote="ToMeK"]riješenja neka možda :D[/quote]
[latex]1.[/latex]ne postoji
[latex]2. k=0[/latex]
[latex]x_1=3, x_2=-3, x_3=0[/latex]
[latex]3. [/latex]lako moguce da sam fulao, ne samo u ovom nego i u drugim zadacima...
[latex]\displaystyle\left( x,y,z\right) \in \{ \left(0,-1+\sqrt{10},-1-\sqrt{10}\right),...,\left(1,\frac{-3-\sqrt{33}}{2},\frac{-3+\sqrt{33}}{2}\right) ,... \}[/latex]
[latex]...[/latex] znaci i permutacije, da ne pisem sad :)
[latex]4. \textrm{??? } p\left( x\right)=\left( x+2\right)^0\cdot \left(3x^3+17x^2+27x+13\right)[/latex]
[latex]5.\displaystyle \frac{3x^2-x+1}{x^4-4x^3+5x^2-4x+4}=\frac{11/25}{x-2}+\frac{11/5}{\left( x-2\right)^2}+\frac{-11x/25-2/25}{x^2+1}[/latex]
[latex]6. p\left( x\right)=6x^3-17x^2+12x[/latex]
| ToMeK (napisa): | riješenja neka možda  |
 ne postoji ne postoji
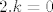
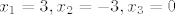
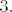 lako moguce da sam fulao, ne samo u ovom nego i u drugim zadacima... lako moguce da sam fulao, ne samo u ovom nego i u drugim zadacima...
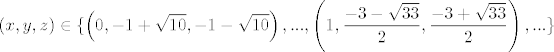
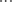 znaci i permutacije, da ne pisem sad znaci i permutacije, da ne pisem sad 
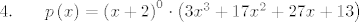
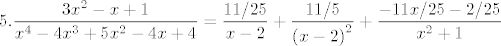
_________________
Mario Berljafa
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
 Postano: 0:04 sri, 4. 2. 2009 Naslov: Postano: 0:04 sri, 4. 2. 2009 Naslov: |
    |
|
|
4. treba napisat kao a(x+2)^3 +b(x+2)^2 +c(x+2) +d. i onda djelis p(x)/(x+2)= h(x) i ostatak koji dobijes je d, pa dijelis h(x)/(x+2) ostatak koji dobijes je c, itd... rjesnje je a=3, b=-1, c=-5, d=3.
p.s. meni se tvoj 5 bas ne slaze, a i c su mi ok 11/25 i -11/25, ali ovi drugi. idem sada jos jednom provjerit. :)
4. treba napisat kao a(x+2)^3 +b(x+2)^2 +c(x+2) +d. i onda djelis p(x)/(x+2)= h(x) i ostatak koji dobijes je d, pa dijelis h(x)/(x+2) ostatak koji dobijes je c, itd... rjesnje je a=3, b=-1, c=-5, d=3.
p.s. meni se tvoj 5 bas ne slaze, a i c su mi ok 11/25 i -11/25, ali ovi drugi. idem sada jos jednom provjerit. 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 1:07 sri, 4. 2. 2009 Naslov: Postano: 1:07 sri, 4. 2. 2009 Naslov: |
    |
|
|
[quote="mycky1111"]4. treba napisat kao a(x+2)^3 +b(x+2)^2 +c(x+2) +d. i onda djelis p(x)/(x+2)= h(x) i ostatak koji dobijes je d, pa dijelis h(x)/(x+2) ostatak koji dobijes je c, itd... rjesnje je a=3, b=-1, c=-5, d=3[/quote] hvala.... to nismo radili, nisam bas kuzio sta se trazi... dobio sam ista rjesenja sad...
[quote="mycky1111"]meni se tvoj 5 bas ne slaze, a i c su mi ok 11/25 i -11/25, ali ovi drugi. idem sada jos jednom provjerit. :)[/quote]ma mozda mi je krivo... i neda mi se sad provjeravat i tako treba bit 50%tna tocnost...
| mycky1111 (napisa): | | 4. treba napisat kao a(x+2)^3 +b(x+2)^2 +c(x+2) +d. i onda djelis p(x)/(x+2)= h(x) i ostatak koji dobijes je d, pa dijelis h(x)/(x+2) ostatak koji dobijes je c, itd... rjesnje je a=3, b=-1, c=-5, d=3 |
hvala.... to nismo radili, nisam bas kuzio sta se trazi... dobio sam ista rjesenja sad...
| mycky1111 (napisa): | meni se tvoj 5 bas ne slaze, a i c su mi ok 11/25 i -11/25, ali ovi drugi. idem sada jos jednom provjerit.  |
ma mozda mi je krivo... i neda mi se sad provjeravat i tako treba bit 50%tna tocnost...
_________________
Mario Berljafa
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
manbearpig
Forumaš(ica)


Pridružen/a: 31. 01. 2009. (19:53:28)
Postovi: (40)16
Spol: 
Lokacija: socijalno nelagodne situacije TAMO SAM
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
PaVla
Forumaš(ica)

Pridružen/a: 18. 09. 2008. (12:04:49)
Postovi: (F)16
Spol: 
|
 Postano: 21:12 sri, 4. 2. 2009 Naslov: Postano: 21:12 sri, 4. 2. 2009 Naslov: |
    |
|
|
[quote="mycky1111"]4. treba napisat kao a(x+2)^3 +b(x+2)^2 +c(x+2) +d. i onda djelis p(x)/(x+2)= h(x) i ostatak koji dobijes je d, pa dijelis h(x)/(x+2) ostatak koji dobijes je c, itd... rjesnje je a=3, b=-1, c=-5, d=3. )[/quote]
tako je i meni ispalo. a ovi svi ostali rezultati mi se slazu s gino-ovim:)
| mycky1111 (napisa): | | 4. treba napisat kao a(x+2)^3 +b(x+2)^2 +c(x+2) +d. i onda djelis p(x)/(x+2)= h(x) i ostatak koji dobijes je d, pa dijelis h(x)/(x+2) ostatak koji dobijes je c, itd... rjesnje je a=3, b=-1, c=-5, d=3. ) |
tako je i meni ispalo. a ovi svi ostali rezultati mi se slazu s gino-ovim:)
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
 Postano: 22:48 sri, 4. 2. 2009 Naslov: Postano: 22:48 sri, 4. 2. 2009 Naslov: |
    |
|
|
[quote="Gino"]
[latex]\textrm{st.}p=n[/latex], sad gledas sta je sa stupnjem sa ljeve i sa desne strane
sad meni dode da je sa desne [latex]n+2[/latex], sa ljeve [latex]max\{4,2n-1\}[/latex], od tud dva slucaja...[/quote]
nisi uzeo u obzir da se taj derivirani polinom množi sa x-1, tako da je onda sa lijeve strane stupanj jednak 2n.
onda iz svega toga slijedi da je stupanj polinoma p jednak n=2.
kao što to uvijek biva, možda je krivo, al mislim da nije :)
| Gino (napisa): |
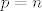 , sad gledas sta je sa stupnjem sa ljeve i sa desne strane , sad gledas sta je sa stupnjem sa ljeve i sa desne strane
sad meni dode da je sa desne  , sa ljeve , sa ljeve 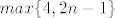 , od tud dva slucaja... , od tud dva slucaja... |
nisi uzeo u obzir da se taj derivirani polinom množi sa x-1, tako da je onda sa lijeve strane stupanj jednak 2n.
onda iz svega toga slijedi da je stupanj polinoma p jednak n=2.
kao što to uvijek biva, možda je krivo, al mislim da nije 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 9:49 čet, 5. 2. 2009 Naslov: Postano: 9:49 čet, 5. 2. 2009 Naslov: |
    |
|
|
e, sam mal, pitanje. kad ireducibilni polinom drugog stupnja ima dvije kompleksne nultočke, kak se to onda zapiše točno?
Ax+B/ireducibilni polinom ili
Ax+B/ireducibilni polinom + Cx+D/ireducibilni polinom na kvadrat
Ak neko skužio šta hoću pitat, može odgovor
e, sam mal, pitanje. kad ireducibilni polinom drugog stupnja ima dvije kompleksne nultočke, kak se to onda zapiše točno?
Ax+B/ireducibilni polinom ili
Ax+B/ireducibilni polinom + Cx+D/ireducibilni polinom na kvadrat
Ak neko skužio šta hoću pitat, može odgovor
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
bucko
Forumaš(ica)


Pridružen/a: 04. 12. 2007. (20:55:30)
Postovi: (A9)16
Spol: 
|
|
| [Vrh] |
|
uzorni student
Forumaš(ica)

Pridružen/a: 24. 01. 2009. (16:11:39)
Postovi: (2C)16
|
|
| [Vrh] |
|
bucko
Forumaš(ica)


Pridružen/a: 04. 12. 2007. (20:55:30)
Postovi: (A9)16
Spol: 
|
|
| [Vrh] |
|
|

















