| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
user11
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (21:08:52)
Postovi: (6)16
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
user11
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (21:08:52)
Postovi: (6)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 22:37 pon, 5. 10. 2009 Naslov: Postano: 22:37 pon, 5. 10. 2009 Naslov: |
    |
|
|
Znam da trebaš indukcijom, ali čisto malo opaska:
5 i 2 su kongruentni -1 modulo 3.
[latex]n[/latex] i [latex]n+1[/latex] su dva uzastopna prirodna broja, pa je sigurno jedan neparan i jedan paran, stoga će [latex]5^n[/latex] i [latex]2^{n+1}[/latex] uvijek jedan biti kongruentan -1, a drugi 1 modulo 3, tj. u zbroju će biti kongruentni 0 modulo 3. To je ono što želimo :)
Znam da trebaš indukcijom, ali čisto malo opaska:
5 i 2 su kongruentni -1 modulo 3.
 i i 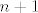 su dva uzastopna prirodna broja, pa je sigurno jedan neparan i jedan paran, stoga će su dva uzastopna prirodna broja, pa je sigurno jedan neparan i jedan paran, stoga će 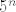 i i 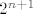 uvijek jedan biti kongruentan -1, a drugi 1 modulo 3, tj. u zbroju će biti kongruentni 0 modulo 3. To je ono što želimo uvijek jedan biti kongruentan -1, a drugi 1 modulo 3, tj. u zbroju će biti kongruentni 0 modulo 3. To je ono što želimo 
|
|
| [Vrh] |
|
user11
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (21:08:52)
Postovi: (6)16
|
 Postano: 10:22 uto, 6. 10. 2009 Naslov: Postano: 10:22 uto, 6. 10. 2009 Naslov: |
    |
|
|
jankri, moram priznat da mi nije trenutno jasno sve sto si napisao, ali samo sam jednom procitao - navecer cu to skuziti, sada se zurim :D
i imam jos jedan problem, dokazivanje bernoullijeve nejednadzbe indukcijom ...
[latex](1+x)^n \ge 1+nx[/latex]
i prvo dokazem za 1,
[latex]1+x \ge 1+x[/latex]
nakon toga pretpostavim da vrijedi:
[latex](1+x)^n \ge 1+nx[/latex]
i onda trebam dokazati da vrijedi za n+1
[latex](1+x)^{n+1} \ge 1+(n+1)x[/latex]
i sada imam u biljeznici
slijedeci korak je ovo
[latex](1+x)^{n+1} \ge (1+x)(n+nx)[/latex]
moze li mi netko pojasniti kako se od [latex]1+(n+1)x[/latex] dodje do [latex](1+x)(n+nx)[/latex]
Hvala !!
jankri, moram priznat da mi nije trenutno jasno sve sto si napisao, ali samo sam jednom procitao - navecer cu to skuziti, sada se zurim 
i imam jos jedan problem, dokazivanje bernoullijeve nejednadzbe indukcijom ...
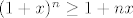
i prvo dokazem za 1,

nakon toga pretpostavim da vrijedi:
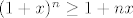
i onda trebam dokazati da vrijedi za n+1

i sada imam u biljeznici
slijedeci korak je ovo

moze li mi netko pojasniti kako se od 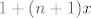 dodje do dodje do 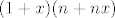
Hvala !!
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
user11
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (21:08:52)
Postovi: (6)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
user11
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (21:08:52)
Postovi: (6)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
user11
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (21:08:52)
Postovi: (6)16
|
|
| [Vrh] |
|
Miriam
Forumaš(ica)

Pridružen/a: 15. 10. 2009. (16:25:04)
Postovi: (D)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 12:42 ned, 18. 10. 2009 Naslov: Postano: 12:42 ned, 18. 10. 2009 Naslov: |
    |
|
|
[quote="Miriam"]da li bih trebala jos dodatno dokazati da je (3^(2k+3) +5) djeljivo sa 8?[/quote]
Da, trebala bi pokazati da je djeljivo sa 8, jer tada će 8(3^(2k+3) +5) u rastavu na proste faktore imati 2^6=64 pa će to biti djeljivo s 64.
Edit: ispravak, treba biti djeljivo sa 8, ne sa 2.
| Miriam (napisa): | | da li bih trebala jos dodatno dokazati da je (3^(2k+3) +5) djeljivo sa 8? |
Da, trebala bi pokazati da je djeljivo sa 8, jer tada će 8(3^(2k+3) +5) u rastavu na proste faktore imati 2^6=64 pa će to biti djeljivo s 64.
Edit: ispravak, treba biti djeljivo sa 8, ne sa 2.
_________________
The Dude Abides
Zadnja promjena: goranm; 19:43 pon, 19. 10. 2009; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Miriam
Forumaš(ica)

Pridružen/a: 15. 10. 2009. (16:25:04)
Postovi: (D)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:44 ned, 18. 10. 2009 Naslov: Postano: 13:44 ned, 18. 10. 2009 Naslov: |
    |
|
|
[quote="Miriam"]54A + 6(2^2k -3k -1)
zanima me da li ovo u zagradi treba dokazati da je isto djeljivo sa 2, ili ??? Mislim, ocito je da je za svako k djeljivo sa 2.
malo mi je nejasno :oops:[/quote]
Da bi 54A + 6(2^2k -3k -1) bilo djeljivo s 54 mora 6(2^2k -3k -1) biti djeljivo s 54.
Jer je rastav od 54 na proste faktore 2*3*3*3, tada ti se u rastavu na proste faktore od 6(2^2k -3k -1) moraju pojaviti 2*3*3*3.
Jer već imaš 6, tada sigurno u rastavu imaš 2*3 pa bi trebala pokazati da 2^2k -3k -1 u svom rastavu ima 3*3, odnosno da je djeljiv s 9, a to opet indukcijom pokažeš.
| Miriam (napisa): | 54A + 6(2^2k -3k -1)
zanima me da li ovo u zagradi treba dokazati da je isto djeljivo sa 2, ili ??? Mislim, ocito je da je za svako k djeljivo sa 2.
malo mi je nejasno  |
Da bi 54A + 6(2^2k -3k -1) bilo djeljivo s 54 mora 6(2^2k -3k -1) biti djeljivo s 54.
Jer je rastav od 54 na proste faktore 2*3*3*3, tada ti se u rastavu na proste faktore od 6(2^2k -3k -1) moraju pojaviti 2*3*3*3.
Jer već imaš 6, tada sigurno u rastavu imaš 2*3 pa bi trebala pokazati da 2^2k -3k -1 u svom rastavu ima 3*3, odnosno da je djeljiv s 9, a to opet indukcijom pokažeš.
_________________
The Dude Abides
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Miriam
Forumaš(ica)

Pridružen/a: 15. 10. 2009. (16:25:04)
Postovi: (D)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
|
















