| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:22 uto, 20. 10. 2009 Naslov: Postano: 0:22 uto, 20. 10. 2009 Naslov: |
    |
|
|
Evo, markotron i ja smo to malo skupa rješavali i nadamo se da nam je rješenje dobro, može li to netko potvrditi?
Zadatak je [url=http://web.math.hr/nastava/uuv/files/uuv-0708-kol1.pdf]ovdje[/url].
Dakle, definiramo [latex]\Omega = \left\{\left(a,\, b\right) \mid \right.[/latex] u prvom izvlačenju je suma iznosa [latex]a[/latex], a u drugom [latex]b;\ a,\, b \in \left\{2,\, 3,\, 4\right\}\left.\right\}[/latex]. (Jasno je da nisu svi događaju u [latex]\Omega[/latex] jednako vjerojatni. Da jesu, zadatak bi bio trivić. :D)
[latex]A = \left\{\left(a\, a\right) \mid a \in \left\{2,\, 3,\, 4\right\}\right\}[/latex].
[latex]H_i = \left\{\left(i,\, b\right) \mid b \in \left\{2,\, 3,\, 4\right\}\right\},\ i \in \left\{2,\, 3,\, 4\right\}[/latex].
Očito, [latex]H_2,\, H_3,\, H_4[/latex] tvore potpun sistem događaja, pa vrijedi
[latex]P\left(A\right)=P\left(A \mid H_2\right) \cdot P\left(H_2\right) + P\left(A \mid H_3\right) \cdot P\left(H_3\right) + P\left(A \mid H_4\right) \cdot P\left(H_4\right)[/latex].
Lako računamo:
[latex]P\left(H_2\right) = \frac{6 \cdot 5}{10 \cdot 9} = \frac{1}{3}[/latex].
[latex]P\left(H_3\right) = \frac{6 \cdot 4 + 4 \cdot 6}{10 \cdot 9} = \frac{8}{15}[/latex].
[latex]P\left(H_4\right) = \frac{4 \cdot 3}{10 \cdot 9} = \frac{2}{15}[/latex].
[latex]P\left(A \mid H_2\right) = \frac{5 \cdot 4}{8 \cdot 7} = \frac{5}{14}[/latex].
[latex]P\left(A \mid H_3\right) = \frac{5 \cdot 3 + 3 \cdot 5}{8 \cdot 7} = \frac{15}{28}[/latex].
[latex]P\left(A \mid H_4\right) = \frac{2 \cdot 1}{8 \cdot 7} = \frac{1}{28}[/latex].
Konačno, [latex]P\left(A\right) = \frac{43}{105} \approx 0.4095[/latex].
Evo, markotron i ja smo to malo skupa rješavali i nadamo se da nam je rješenje dobro, može li to netko potvrditi?
Zadatak je ovdje.
Dakle, definiramo 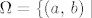 u prvom izvlačenju je suma iznosa u prvom izvlačenju je suma iznosa  , a u drugom , a u drugom 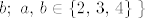 . (Jasno je da nisu svi događaju u . (Jasno je da nisu svi događaju u 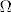 jednako vjerojatni. Da jesu, zadatak bi bio trivić. jednako vjerojatni. Da jesu, zadatak bi bio trivić.  ) )
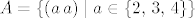 . .
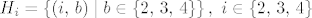 . .
Očito, 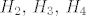 tvore potpun sistem događaja, pa vrijedi tvore potpun sistem događaja, pa vrijedi
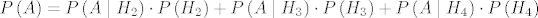 . .
Lako računamo:
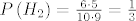 . .
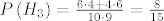 . .
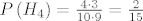 . .
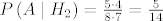 . .
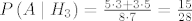 . .
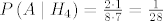 . .
Konačno, 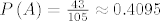 . .
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
babybodom
Forumaš(ica)
Pridružen/a: 29. 06. 2009. (22:03:01)
Postovi: (31)16
Lokacija: zagreb
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
 Postano: 19:12 uto, 20. 10. 2009 Naslov: Postano: 19:12 uto, 20. 10. 2009 Naslov: |
    |
|
|
[latex]H_i[/latex], kako pise u JANKRI-jevom postu, je događaj da je u prvom izvlačenju dobivena suma i. Dakle [latex]H_2[/latex] je događaj da je prva suma 2, a ekvivalentno je reći da su prve dvije izvučene kovanice od 1 kune. [latex]H_3[/latex] događaj kad su u prvom izvlačenju izvučene različite kovanice (1 i 2 u bilo kom poretku). [latex]H_4[/latex] je, pogađaš, događaj u kojem su u prvom izvlačenju izvučene dvije kovanice od 2 kune. Jasnije?
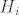 , kako pise u JANKRI-jevom postu, je događaj da je u prvom izvlačenju dobivena suma i. Dakle , kako pise u JANKRI-jevom postu, je događaj da je u prvom izvlačenju dobivena suma i. Dakle 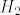 je događaj da je prva suma 2, a ekvivalentno je reći da su prve dvije izvučene kovanice od 1 kune. je događaj da je prva suma 2, a ekvivalentno je reći da su prve dvije izvučene kovanice od 1 kune. 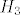 događaj kad su u prvom izvlačenju izvučene različite kovanice (1 i 2 u bilo kom poretku). događaj kad su u prvom izvlačenju izvučene različite kovanice (1 i 2 u bilo kom poretku). 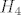 je, pogađaš, događaj u kojem su u prvom izvlačenju izvučene dvije kovanice od 2 kune. Jasnije? je, pogađaš, događaj u kojem su u prvom izvlačenju izvučene dvije kovanice od 2 kune. Jasnije?
_________________
Jedan je smjer očit, a drugi je trivijalan.
|
|
| [Vrh] |
|
babybodom
Forumaš(ica)
Pridružen/a: 29. 06. 2009. (22:03:01)
Postovi: (31)16
Lokacija: zagreb
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
 Postano: 23:43 uto, 20. 10. 2009 Naslov: Postano: 23:43 uto, 20. 10. 2009 Naslov: |
    |
|
|
malo drukčiji pristup (diskretno)
jedini slučajevi kada su sume jednake su sljedeći
1. 11 11
2. 21 21
3. 12 12
4. 21 12
5. 12 21
6. 22 22
2. slučaj primjerice znači da smo u prvom izvlačenju izvukli 2 u drugom 1 u trećem 2 i u četvrtom opet 2....
i sada je samo pitanje na koliko se načina može odabrati pojedini slučaj, posumirati sve to i podijeliti sa omega
1. prvu jedinicu na 6, drugu na 4, treću na 3 četvrtu na 2 načina = 6*5*4*3
2. 3. 4. i 5. su ekvivalentni i jednaki su pojedinačno jednu dvojku na 4 načina, drugu na 3 prvu jedinicu na 6 drugu na 5 načina...znači jednako je 6*4*5*3
sva 4 slučaja ćemo dobit ako sve pomnožimo s 4 znači 6*4*4*5*3
i 5. slučaj analgno =4*3*2*1
omega je očito 10*9*8*7
i sad tražena vjerojatnost je (6*5*4*3+4*4*6*5*3+4*3*2*1)/10*9*8*7=0,3619...
malo drukčiji pristup (diskretno)
jedini slučajevi kada su sume jednake su sljedeći
1. 11 11
2. 21 21
3. 12 12
4. 21 12
5. 12 21
6. 22 22
2. slučaj primjerice znači da smo u prvom izvlačenju izvukli 2 u drugom 1 u trećem 2 i u četvrtom opet 2....
i sada je samo pitanje na koliko se načina može odabrati pojedini slučaj, posumirati sve to i podijeliti sa omega
1. prvu jedinicu na 6, drugu na 4, treću na 3 četvrtu na 2 načina = 6*5*4*3
2. 3. 4. i 5. su ekvivalentni i jednaki su pojedinačno jednu dvojku na 4 načina, drugu na 3 prvu jedinicu na 6 drugu na 5 načina...znači jednako je 6*4*5*3
sva 4 slučaja ćemo dobit ako sve pomnožimo s 4 znači 6*4*4*5*3
i 5. slučaj analgno =4*3*2*1
omega je očito 10*9*8*7
i sad tražena vjerojatnost je (6*5*4*3+4*4*6*5*3+4*3*2*1)/10*9*8*7=0,3619...
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
 Postano: 16:03 uto, 10. 11. 2009 Naslov: Postano: 16:03 uto, 10. 11. 2009 Naslov: |
    |
|
|
u JANKRI-jevon objasnjenju, kad racunamo P(Hi), npr P(H2) gledamo da postoji 6 nacina za izvuc 1 kn,i onda 5 nacina za izvuc 1 kn. A zasto zanemarujemo sumu b (koja moze bit 2,3,4)... :S:S Hvala:)
u JANKRI-jevon objasnjenju, kad racunamo P(Hi), npr P(H2) gledamo da postoji 6 nacina za izvuc 1 kn,i onda 5 nacina za izvuc 1 kn. A zasto zanemarujemo sumu b (koja moze bit 2,3,4)... :S:S Hvala:)
|
|
| [Vrh] |
|
|









