| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 13:44 ned, 11. 4. 2010 Naslov: Postano: 13:44 ned, 11. 4. 2010 Naslov: |
    |
|
|
1. b) Traze se sve stacionarne tocke, tj oni x-evi za koje je y'(x)=0.
Sad deriviramo onu implicitno zadanu funkciju i dobijemo
2xy^3 + (1+x^2)*3y'y^2+y'-2x=0
Trazimo tocke u kojima je y'=0, pa to i uvrstimo... dobije se
2xy^3-2x=0, iz cega dobivamo x=0 ili y^3=1
Probamo oba slucaja:
I: x=0 (uvrstimo u pocetnu formulu)=> y^3+y=0 => y=0 (dakle, tocka je x=0, y(x)=0)
II: y^3=1 => y=1 (opet uvrstimo i dobijemo kontradikciju), dakle ovaj prvi slucaj daje jedino rjesenje: (0,0)
2. Ako se dodiruju => imaju zajednicku tangentu => tangente u toj tocki imaju jednak koeficijent smjera => derivacije u toj tocki su jednake
Zbog toga deriviramo obje funkcije i dobijemo:
(oznacili smo ova 2 ipsilona s y1, y2 da ih razlikujemo)
y1'=x^2 +1
y2'=3x-1
Derivacije moraju biti jednake, dakle tocke dodira se nalaze medju rjesenjima jednadzbe x^2+1=3x-1 (a to su 1 i 2)
Sad samo provjerimo dal su u tockama x=1, x=2 jednake funkcijske vrijednosti (ipsiloni):
y1(1)=14/6, y2(1)=14/6 (dakle 1 je stvarno tocka dodira)
u drugom slucaju
y1(2)=34/6, y2(2)=35/6 (=> 2 nije tocka dodira)
1. b) Traze se sve stacionarne tocke, tj oni x-evi za koje je y'(x)=0.
Sad deriviramo onu implicitno zadanu funkciju i dobijemo
2xy^3 + (1+x^2)*3y'y^2+y'-2x=0
Trazimo tocke u kojima je y'=0, pa to i uvrstimo... dobije se
2xy^3-2x=0, iz cega dobivamo x=0 ili y^3=1
Probamo oba slucaja:
I: x=0 (uvrstimo u pocetnu formulu)=> y^3+y=0 => y=0 (dakle, tocka je x=0, y(x)=0)
II: y^3=1 => y=1 (opet uvrstimo i dobijemo kontradikciju), dakle ovaj prvi slucaj daje jedino rjesenje: (0,0)
2. Ako se dodiruju => imaju zajednicku tangentu => tangente u toj tocki imaju jednak koeficijent smjera => derivacije u toj tocki su jednake
Zbog toga deriviramo obje funkcije i dobijemo:
(oznacili smo ova 2 ipsilona s y1, y2 da ih razlikujemo)
y1'=x^2 +1
y2'=3x-1
Derivacije moraju biti jednake, dakle tocke dodira se nalaze medju rjesenjima jednadzbe x^2+1=3x-1 (a to su 1 i 2)
Sad samo provjerimo dal su u tockama x=1, x=2 jednake funkcijske vrijednosti (ipsiloni):
y1(1)=14/6, y2(1)=14/6 (dakle 1 je stvarno tocka dodira)
u drugom slucaju
y1(2)=34/6, y2(2)=35/6 (=> 2 nije tocka dodira)
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kikyca
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (18:45:07)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 11:42 pon, 12. 4. 2010 Naslov: Postano: 11:42 pon, 12. 4. 2010 Naslov: |
    |
|
|
Implicitno deriviraš, uvrstiš y'=0, nađeš uvjet za x i y, uvrstiš ga u početnu jednakost. Dobi se točka [latex](\sqrt{e},\frac{1}{\sqrt{e}})[/latex].
EDIT: Naravno, još bi trebalo provjeriti dobiveno rješenje. Pokazali smo da vrijedi implikacija [latex]y'=0 \Rightarrow x=\sqrt{e}\ \&\ y=\frac{1}{\sqrt{e}}[/latex], ali ne i obrat, pa je provjera nužna.
Implicitno deriviraš, uvrstiš y'=0, nađeš uvjet za x i y, uvrstiš ga u početnu jednakost. Dobi se točka 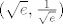 . .
EDIT: Naravno, još bi trebalo provjeriti dobiveno rješenje. Pokazali smo da vrijedi implikacija 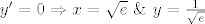 , ali ne i obrat, pa je provjera nužna. , ali ne i obrat, pa je provjera nužna.
|
|
| [Vrh] |
|
|









