nije mi bas jasno kako se izracuna integral po onim malim polukruznicama koje obilaze singularitete na realnoj osi. u biljeznici mi pise da je prvo potrebno rastaviti podintegralnu funkciju na analiticki dio i posebno ostatak i onda taj analiticki dio pokazemo da ide u 0 kad se radijus polukruznice smanjuje prema 0. a ostatak integriramo normalno kao kompleksnu funkciju. dobro, kad ovak napisem, sve mi je jasno kakti, medjutim ne mogu rijesit ni jedan zadatak :lol:
evo, npr ovaj zadatak, s njim imam vise problema (to je inace sa roka 20.02.2008., 3. zadatak):
[latex] \int_{-\infty}^{\infty} \frac{cos x}{x^5+x^4+x+1} dx [/latex]
joj, ovo ce biti tako dugacak i dosadan post.
dobro, sad prvo se prosiri funkc bla bla bla, sigulariteti koji su unutar [latex] \Gamma_{R}[/latex] su -1, [latex]\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}, \frac{-\sqrt{2}}{2}+i\frac{\sqrt{2}}{2} [/latex]
i evo, vec prvi problem mi je izracunat integral po [latex] \Gamma_{R}[/latex] - kako da najbrze izracunam na ovom konkretnom primjeru reziduume u te 2 tocke?? nekak je sve skupa ruzno, izracunala sam ih zapravo, ali ih ne zelim zbrojit jer cu dobit katastrofu
drugi problem mi je ovaj iz naslova. dakle, trebam razviti [latex]\frac{e^{iz}}{(z+1)(z^4+1)} [/latex] u red oko -1. jel mogu zakljucit da [latex]e^{iz}[/latex] i [latex]\frac{1}{z^4+1}[/latex] imaju razvoj u Taylorov red oko -1 i uopce ih ne dirat ni nis, nego napisat da je [latex] f(z) = \frac{Res(f, -1)}{z+1} + g(z)[/latex] gdje je g analiticka... ?? ako je to u redu, onda bi dalje znala.
nije mi bas jasno kako se izracuna integral po onim malim polukruznicama koje obilaze singularitete na realnoj osi. u biljeznici mi pise da je prvo potrebno rastaviti podintegralnu funkciju na analiticki dio i posebno ostatak i onda taj analiticki dio pokazemo da ide u 0 kad se radijus polukruznice smanjuje prema 0. a ostatak integriramo normalno kao kompleksnu funkciju. dobro, kad ovak napisem, sve mi je jasno kakti, medjutim ne mogu rijesit ni jedan zadatak 
evo, npr ovaj zadatak, s njim imam vise problema (to je inace sa roka 20.02.2008., 3. zadatak):
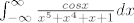
joj, ovo ce biti tako dugacak i dosadan post.
dobro, sad prvo se prosiri funkc bla bla bla, sigulariteti koji su unutar 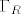 su -1,
su -1, 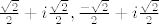
i evo, vec prvi problem mi je izracunat integral po 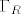 - kako da najbrze izracunam na ovom konkretnom primjeru reziduume u te 2 tocke?? nekak je sve skupa ruzno, izracunala sam ih zapravo, ali ih ne zelim zbrojit jer cu dobit katastrofu
- kako da najbrze izracunam na ovom konkretnom primjeru reziduume u te 2 tocke?? nekak je sve skupa ruzno, izracunala sam ih zapravo, ali ih ne zelim zbrojit jer cu dobit katastrofu
drugi problem mi je ovaj iz naslova. dakle, trebam razviti 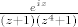 u red oko -1. jel mogu zakljucit da
u red oko -1. jel mogu zakljucit da 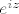 i
i 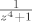 imaju razvoj u Taylorov red oko -1 i uopce ih ne dirat ni nis, nego napisat da je
imaju razvoj u Taylorov red oko -1 i uopce ih ne dirat ni nis, nego napisat da je 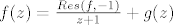 gdje je g analiticka... ?? ako je to u redu, onda bi dalje znala.
gdje je g analiticka... ?? ako je to u redu, onda bi dalje znala.
_________________
Nov, još gluplji.




