| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
i_dumba19
Forumaš(ica)
Pridružen/a: 10. 11. 2009. (20:23:34)
Postovi: (1E)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
i_dumba19
Forumaš(ica)
Pridružen/a: 10. 11. 2009. (20:23:34)
Postovi: (1E)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:58 sub, 27. 11. 2010 Naslov: Postano: 21:58 sub, 27. 11. 2010 Naslov: |
    |
|
|
[quote="i_dumba19"]mozemo za par n-ova vidjeti koji je otprilike supremum odnosno infimum?[/quote]
Može, ali ne znam koliko je to sigurna metoda.
Uvijek je dobro (ako ne i nužno) odrediti kako "izgleda" taj skup. U ovom slučaju, imamo niz, pa se to svodi na određivanje intervala rasta i pada.
Uzmimo [latex]\displaystyle A = \left\{ \frac{3 n + 7}{4 n + 2} : n \in \mathbb{N} \right\}[/latex] i [latex]\displaystyle a_n = \frac{3 n + 7}{4 n + 2}[/latex], za [latex]n \in \mathbb{N}[/latex]. Lako se pokaže da je [latex]a_n > a_{n + 1} \ \Leftrightarrow \ 42 > 20[/latex]. Dakle, niz [latex](a_n)[/latex] je strogo padajući. Sad je očito [latex]\displaystyle \inf A = \lim_{n \to +\infty} a_n = \frac{3}{4}[/latex] i [latex]\displaystyle \sup A = a_1 = \frac{10}{6} = \frac{5}{3}[/latex].
Mogu se pojaviti neki kompliciraniji primjeri, gdje nakon određivanja intervala rasta i pada nije baš očito što bi bio infimum, a što supremum. Tada si je dobro nacrtati ono o čemu se radi (barem mentalno). Tu [url=http://www.wolframalpha.com/]WolframAlpha[/url] može dobro doći. Za ovaj primjer, moglo bi se upisati ListPlot[Table[(3 n + 7)/(4 n + 2), {n, 1, 20}]].
| i_dumba19 (napisa): | | mozemo za par n-ova vidjeti koji je otprilike supremum odnosno infimum? |
Može, ali ne znam koliko je to sigurna metoda.
Uvijek je dobro (ako ne i nužno) odrediti kako "izgleda" taj skup. U ovom slučaju, imamo niz, pa se to svodi na određivanje intervala rasta i pada.
Uzmimo 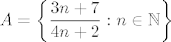 i i 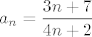 , za , za  . Lako se pokaže da je . Lako se pokaže da je 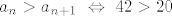 . Dakle, niz . Dakle, niz 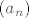 je strogo padajući. Sad je očito je strogo padajući. Sad je očito 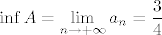 i i 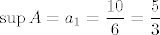 . .
Mogu se pojaviti neki kompliciraniji primjeri, gdje nakon određivanja intervala rasta i pada nije baš očito što bi bio infimum, a što supremum. Tada si je dobro nacrtati ono o čemu se radi (barem mentalno). Tu WolframAlpha može dobro doći. Za ovaj primjer, moglo bi se upisati ListPlot[Table[(3 n + 7)/(4 n + 2), {n, 1, 20}]].
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
 Postano: 21:17 uto, 30. 11. 2010 Naslov: Postano: 21:17 uto, 30. 11. 2010 Naslov: |
    |
|
|
[quote="pmli"][quote="i_dumba19"]mozemo za par n-ova vidjeti koji je otprilike supremum odnosno infimum?[/quote]
Može, ali ne znam koliko je to sigurna metoda.
Uvijek je dobro (ako ne i nužno) odrediti kako "izgleda" taj skup. U ovom slučaju, imamo niz, pa se to svodi na određivanje intervala rasta i pada.
Uzmimo [latex]\displaystyle A = \left\{ \frac{3 n + 7}{4 n + 2} : n \in \mathbb{N} \right\}[/latex] i [latex]\displaystyle a_n = \frac{3 n + 7}{4 n + 2}[/latex], za [latex]n \in \mathbb{N}[/latex]. Lako se pokaže da je [latex]a_n > a_{n + 1} \ \Leftrightarrow \ 42 > 20[/latex]. Dakle, niz [latex](a_n)[/latex] je strogo padajući. Sad je očito [latex]\displaystyle \inf A = \lim_{n \to +\infty} a_n = \frac{3}{4}[/latex] i [latex]\displaystyle \sup A = a_1 = \frac{10}{6} = \frac{5}{3}[/latex].
Mogu se pojaviti neki kompliciraniji primjeri, gdje nakon određivanja intervala rasta i pada nije baš očito što bi bio infimum, a što supremum. Tada si je dobro nacrtati ono o čemu se radi (barem mentalno). Tu [url=http://www.wolframalpha.com/]WolframAlpha[/url] može dobro doći. Za ovaj primjer, moglo bi se upisati ListPlot[Table[(3 n + 7)/(4 n + 2), {n, 1, 20}]].[/quote]
kak si dobio infA?
| pmli (napisa): | | i_dumba19 (napisa): | | mozemo za par n-ova vidjeti koji je otprilike supremum odnosno infimum? |
Može, ali ne znam koliko je to sigurna metoda.
Uvijek je dobro (ako ne i nužno) odrediti kako "izgleda" taj skup. U ovom slučaju, imamo niz, pa se to svodi na određivanje intervala rasta i pada.
Uzmimo 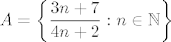 i i 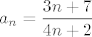 , za , za  . Lako se pokaže da je . Lako se pokaže da je 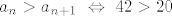 . Dakle, niz . Dakle, niz 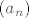 je strogo padajući. Sad je očito je strogo padajući. Sad je očito 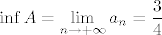 i i 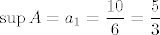 . .
Mogu se pojaviti neki kompliciraniji primjeri, gdje nakon određivanja intervala rasta i pada nije baš očito što bi bio infimum, a što supremum. Tada si je dobro nacrtati ono o čemu se radi (barem mentalno). Tu WolframAlpha može dobro doći. Za ovaj primjer, moglo bi se upisati ListPlot[Table[(3 n + 7)/(4 n + 2), {n, 1, 20}]]. |
kak si dobio infA?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:02 uto, 30. 11. 2010 Naslov: Postano: 22:02 uto, 30. 11. 2010 Naslov: |
    |
|
|
[quote="Buki"]kak si dobio infA?[/quote]
Misliš na limes? To je jednostavni limes racionalne funkcije. Kako su u brojniku i nazivniku polinomi jednakog stupnja, slijedi da je limes jednak omjeru vodećih koeficijenata. Na dugačko, to ni išlo ovako: [latex]\displaystyle \lim_{n \to +\infty} \frac{3 n + 7}{4 n + 2} : \frac{n}{n} = \lim_{n \to +\infty} \frac{3 + \frac{7}{n}}{4 + \frac{2}{n}} = \frac{3 + 0}{4 + 0} = \frac{3}{4}[/latex]. To je nepotrebno, tako da čim dobiš takvi limes, samo napiši rezultat. Čak i imate tako zapisan limes u [url=http://web.math.hr/nastava/analiza/files/formule.pdf]formulama dopuštenim na kolokvijima[/url].
Ako si pitao sa čisto teoretskog stajališta (kako sam zaključio da je infimum baš limes tog nekog niza), odgovor je dan na predavanju. Može se pokazati da je padajući i ograničen niz konvergentan, te da mu je limes točno infimum slike tog niza.
| Buki (napisa): | | kak si dobio infA? |
Misliš na limes? To je jednostavni limes racionalne funkcije. Kako su u brojniku i nazivniku polinomi jednakog stupnja, slijedi da je limes jednak omjeru vodećih koeficijenata. Na dugačko, to ni išlo ovako: 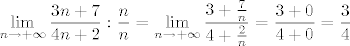 . To je nepotrebno, tako da čim dobiš takvi limes, samo napiši rezultat. Čak i imate tako zapisan limes u formulama dopuštenim na kolokvijima. . To je nepotrebno, tako da čim dobiš takvi limes, samo napiši rezultat. Čak i imate tako zapisan limes u formulama dopuštenim na kolokvijima.
Ako si pitao sa čisto teoretskog stajališta (kako sam zaključio da je infimum baš limes tog nekog niza), odgovor je dan na predavanju. Može se pokazati da je padajući i ograničen niz konvergentan, te da mu je limes točno infimum slike tog niza.
|
|
| [Vrh] |
|
kapetan
Forumaš(ica)

Pridružen/a: 03. 11. 2010. (00:01:56)
Postovi: (2)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:21 sri, 5. 1. 2011 Naslov: Postano: 13:21 sri, 5. 1. 2011 Naslov: |
    |
|
|
Okej, prvo da riješimo par stvari. :P Skup je sam po sebi neuređen objekt, pa ne možeš reći da je rastući, a ni padajući. I da, znam što si mislila. :D Da imamo neku funkciju koja, u biti, definira taj skup, a koja je rastuća/padajuća, jel tak? :) Ali dobro, samo sam htio reći da je objava da je skup rastuć/padajuć nemalo zlorabljenje terminologije.
No dobro, kad ćemo već biti sitničavi, i [latex]S=A\cdot B[/latex] je sitno zlorabljenje notacije budući da na skupovima nije definirana operacija množenja u ovom smislu u kojem je tu koristimo. Ali dobro, ponovno je jasno što si mislila... :)
Okej, a sad na pitanje. Dakle, imamo skupove [latex]A[/latex] i [latex]B[/latex] i zanimaju nas supremum i infimum njihovog "umnoška". Naravno, da bismo mogli koristiti ovo što dalje slijedi, [latex]A[/latex] i [latex]B[/latex] moraju biti "neovisni" - u ovim tu zadacima to se uglavnom svodi na to da [latex]A[/latex] ovisi samo o jednoj varijabli, a [latex]B[/latex] o drugoj. Na primjer, za [latex]\displaystyle\{\frac{1}{mn-1}\cdot\frac{1}{m-0.5}:m,n\in\mathbb{N}\}[/latex] očiti rastav (prvi razlomak "u prvi skup", a drugi "u drugi") nije dobar jer oni nisu neovisni.
Ako je i sad sve u redu, što bi reklo da su [latex]A[/latex] i [latex]B[/latex] neovisni (i recimo ograničeni, da se sad ne mučimo s [latex]\infty[/latex], makar i tu možemo nešto zaključivati), možemo reći ovo:
[latex]\sup{S}=\max\{\sup{A}\sup{B},\sup{A}\inf{B},\inf{A}\sup{B},\inf{A}\inf{B}\}[/latex], a [latex]\inf{S}=\min\{\sup{A}\sup{B},\sup{A}\inf{B},\inf{A}\sup{B},\inf{A}\inf{B}\}[/latex]. To je nekako, kad razmisliš, dosta intuitivno, a i da se dokazati dosta lako.
To je vjerojatno ta formula koju si tražila. E, a to s "rastom" ili "padom" nema neke direktne veze, samo što nam oni mogu pomoći pri određivanju supremuma i infimuma skupova [latex]A[/latex] i [latex]B[/latex]. Specifično, ako je skup [latex]T[/latex] "definiran" rastućim nizom [latex](t_n)_n[/latex], tada je [latex]\inf T=t_1[/latex], a [latex]\sup T=\displaystyle\lim_{n}t_n[/latex], pri čemu supremum ovdje može biti i [latex]+\infty[/latex]. To dokažeš gotovo pa trivijalno. Potpuno analogno, ako je [latex]T[/latex] "definiran" padajućim nizom [latex](t_n)_n[/latex], tada je [latex]\sup T=t_1[/latex], a [latex]\inf T=\displaystyle\lim_{n}t_n[/latex]. Naravno, to ovaj put može biti i [latex]-\infty[/latex].
Evo, sve ove stvari gore su, kažem, relativno lake za dokazati, pitaj ako treba što. :)
Okej, prvo da riješimo par stvari.  Skup je sam po sebi neuređen objekt, pa ne možeš reći da je rastući, a ni padajući. I da, znam što si mislila. Skup je sam po sebi neuređen objekt, pa ne možeš reći da je rastući, a ni padajući. I da, znam što si mislila.  Da imamo neku funkciju koja, u biti, definira taj skup, a koja je rastuća/padajuća, jel tak? Da imamo neku funkciju koja, u biti, definira taj skup, a koja je rastuća/padajuća, jel tak?  Ali dobro, samo sam htio reći da je objava da je skup rastuć/padajuć nemalo zlorabljenje terminologije. Ali dobro, samo sam htio reći da je objava da je skup rastuć/padajuć nemalo zlorabljenje terminologije.
No dobro, kad ćemo već biti sitničavi, i 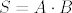 je sitno zlorabljenje notacije budući da na skupovima nije definirana operacija množenja u ovom smislu u kojem je tu koristimo. Ali dobro, ponovno je jasno što si mislila... je sitno zlorabljenje notacije budući da na skupovima nije definirana operacija množenja u ovom smislu u kojem je tu koristimo. Ali dobro, ponovno je jasno što si mislila... 
Okej, a sad na pitanje. Dakle, imamo skupove  i i  i zanimaju nas supremum i infimum njihovog "umnoška". Naravno, da bismo mogli koristiti ovo što dalje slijedi, i zanimaju nas supremum i infimum njihovog "umnoška". Naravno, da bismo mogli koristiti ovo što dalje slijedi,  i i  moraju biti "neovisni" - u ovim tu zadacima to se uglavnom svodi na to da moraju biti "neovisni" - u ovim tu zadacima to se uglavnom svodi na to da  ovisi samo o jednoj varijabli, a ovisi samo o jednoj varijabli, a  o drugoj. Na primjer, za o drugoj. Na primjer, za 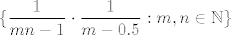 očiti rastav (prvi razlomak "u prvi skup", a drugi "u drugi") nije dobar jer oni nisu neovisni. očiti rastav (prvi razlomak "u prvi skup", a drugi "u drugi") nije dobar jer oni nisu neovisni.
Ako je i sad sve u redu, što bi reklo da su  i i  neovisni (i recimo ograničeni, da se sad ne mučimo s neovisni (i recimo ograničeni, da se sad ne mučimo s 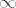 , makar i tu možemo nešto zaključivati), možemo reći ovo: , makar i tu možemo nešto zaključivati), možemo reći ovo:
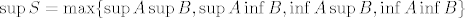 , a , a 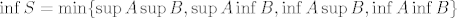 . To je nekako, kad razmisliš, dosta intuitivno, a i da se dokazati dosta lako. . To je nekako, kad razmisliš, dosta intuitivno, a i da se dokazati dosta lako.
To je vjerojatno ta formula koju si tražila. E, a to s "rastom" ili "padom" nema neke direktne veze, samo što nam oni mogu pomoći pri određivanju supremuma i infimuma skupova  i i  . Specifično, ako je skup . Specifično, ako je skup  "definiran" rastućim nizom "definiran" rastućim nizom 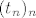 , tada je , tada je 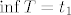 , a , a 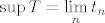 , pri čemu supremum ovdje može biti i , pri čemu supremum ovdje može biti i  . To dokažeš gotovo pa trivijalno. Potpuno analogno, ako je . To dokažeš gotovo pa trivijalno. Potpuno analogno, ako je  "definiran" padajućim nizom "definiran" padajućim nizom 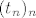 , tada je , tada je 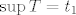 , a , a 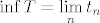 . Naravno, to ovaj put može biti i . Naravno, to ovaj put može biti i 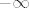 . .
Evo, sve ove stvari gore su, kažem, relativno lake za dokazati, pitaj ako treba što. 
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:26 čet, 6. 1. 2011 Naslov: Postano: 19:26 čet, 6. 1. 2011 Naslov: |
    |
|
|
Dobro, to se tu negdje spominjalo po forumima, ali nisam vidio ni jedno kompletno objašnjenje, pa da vidimo... :)
Dakle, biraj grupu. Prva? Druga? OK, druga. :D (Mislim, isto je potpuno, da se ne zavaravamo. :D)
Ovaj zadatak sadrži tri od nekakve četiri ideje za traženje infimuma/supremuma koje se ja u ovom trenutku mogu sjetiti. Prva je vezana uz ovaj arkus tangens. Primijetit ćeš da je to rastuća funkcija, što znači da, ako s [latex]T[/latex] označimo [latex]\displaystyle\{\frac{(-1)^n2n+1}{n^2\cos(n\pi)}:n\in\mathbb{N}\}[/latex], vrijedi [latex]\sup S=\mathrm{arctg }(\sup T)[/latex] i [latex]\inf S=\mathrm{arctg }(\inf T)[/latex]. Takvu stvar ste sigurno spominjali na vježbama - dokazivali ne znam jeste li, ali nije teško, intuitivno je dosta jasno, mislim. Reci ako treba.
U svakom slučaju, zaključujemo da nas samo zanimaju supremum i infimum od [latex]T[/latex]. U ovom trenutku u igru ulazi druga česta ideja: particioniranje skupa na nekoliko manjih. Specifično, prikazat ćemo [latex]T:=A\cup B[/latex], pri čemu će [latex]A[/latex] biti zadan istom formulom kao [latex]T[/latex], samo za parne [latex]n[/latex], a [latex]B[/latex] za neparne. Motivacija za ovo je dosta jasna: ova potencija od [latex]-1[/latex] sjeionako uvijek ili [latex]1[/latex] ili [latex]-1[/latex], pa idemo gledati te slučajeve odvojeno, kad već možemo. Također, vidimo da će nam ovo pomoći sa kosinusom u nazivniku.
Znamo (ponovno, sigurno ste rekli/dokazivali na vježbama, reci ako treba što objasniti) da vrijedi [latex]\sup T=\max\{\sup A, \sup B\}[/latex] i [latex]\inf T=\min\{\inf A, \inf B\}[/latex]. Dakle, bit će nam dovoljno znati infimume i supremume ova dva manja skupa.
Kod tih ulazi napokon i treća ideja koju ćemo spominjati. Naime, pogledajmo kako [latex]A[/latex] izgleda. To je zapravo, kad se riješimo svih kerefeka, skup [latex]\{\displaystyle\frac{4k+1}{4k^2}: k\in\mathbb{N}\}[/latex] (tu smo uzimali [latex]n=2k[/latex], čime "pokrivamo" točno sve parne prirodne [latex]n[/latex]).
E, a za ovaj pripadajući niz (definiran s [latex]a_k=\displaystyle\frac{1}{k}+\frac{1}{4k^2}[/latex]) mi možemo reći da je padajuć. Naime, oba pribrojnika su mu padajuća. Stoga, (ponovno, po lako dokazivoj stvari koju ste sigurno radili na vježbama i koja je intuitivno dosta jasna), [latex]\sup A=a_1=\displaystyle\frac{5}{4}[/latex], a [latex]\inf A=\displaystyle\lim_{k}a_k=0[/latex].
Dobro, preostaje nam još jedino skup [latex]B[/latex]. Ponovno, kad se riješimo kosinusa (jer znamo koliko je to kosinus od "neparno" pijeva), dobivamo da je [latex]B=\displaystyle\{\frac{2(2k-1)-1}{(2k-1)^2}:k\in\mathbb{N}\}[/latex] (tu uzimamo, s istom argumentacijom kao gore, [latex]n=2k-1[/latex]).
E, dobro, tu će stvar biti malo ružnija nego u prvom skupu, ali i dalje rješiva. Dakle, tvrdimo da je i niz definiran s [latex]b_k=\displaystyle\frac{4k-3}{(2k-1)^2}[/latex] padajuć. Dokažimo to: direktno ćemo provjeriti vrijedi li uvijek [latex]a_k\geq a_{k+1}[/latex]. To je očito ekvivalentno s [latex](2(2k-1)-1)(2k+1)^2\geq (2(2k+1)-1)(2k-1)^2[/latex]. E, sad, kad se to raspiše dobivamo (valjda :D) da je to ekvivalentno s [latex]16k^3+4k^2-8k-3\geq 16k^3-12k^2+1[/latex], tj. s [latex]4k^2\geq 2k+1[/latex]. To, naravno, očito vrijedi, što nam je valjda najlakše vidjeti (ili barem meni najlakše zapisati :D) ako prikažemo u obliku [latex](2k-0.5)^2+0.75\geq 0[/latex] (kako god išla, indukcijom, direktnim rješavanjem kvadratne čime već, svejedno je... :)).
Stoga, koristeći istu argumentaciju kao za [latex]A[/latex], vrijedi [latex]\sup B=b_1=1[/latex] i [latex]\inf B=\displaystyle\lim_{k}b_k=0[/latex].
Sad smo gotovi. Naime, onda znamo da je [latex]\sup T=\max\{1.25,1\}=1.25[/latex], a [latex]\inf T=\min\{0,0\}=0[/latex], pa je [latex]\sup S=\mathrm{arctg } 1.25[/latex], a [latex]\inf S=\mathrm{arctg } 0=0[/latex].
Evo, i to bi bilo kao to. Mislim da su razlozi zašto neću pisati drugu grupu u ovom trenutku očiti. :D
Dobro, to se tu negdje spominjalo po forumima, ali nisam vidio ni jedno kompletno objašnjenje, pa da vidimo... 
Dakle, biraj grupu. Prva? Druga? OK, druga.  (Mislim, isto je potpuno, da se ne zavaravamo. (Mislim, isto je potpuno, da se ne zavaravamo.  ) )
Ovaj zadatak sadrži tri od nekakve četiri ideje za traženje infimuma/supremuma koje se ja u ovom trenutku mogu sjetiti. Prva je vezana uz ovaj arkus tangens. Primijetit ćeš da je to rastuća funkcija, što znači da, ako s  označimo označimo 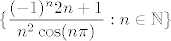 , vrijedi , vrijedi 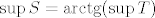 i i 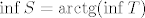 . Takvu stvar ste sigurno spominjali na vježbama - dokazivali ne znam jeste li, ali nije teško, intuitivno je dosta jasno, mislim. Reci ako treba. . Takvu stvar ste sigurno spominjali na vježbama - dokazivali ne znam jeste li, ali nije teško, intuitivno je dosta jasno, mislim. Reci ako treba.
U svakom slučaju, zaključujemo da nas samo zanimaju supremum i infimum od  . U ovom trenutku u igru ulazi druga česta ideja: particioniranje skupa na nekoliko manjih. Specifično, prikazat ćemo . U ovom trenutku u igru ulazi druga česta ideja: particioniranje skupa na nekoliko manjih. Specifično, prikazat ćemo 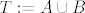 , pri čemu će , pri čemu će  biti zadan istom formulom kao biti zadan istom formulom kao  , samo za parne , samo za parne  , a , a  za neparne. Motivacija za ovo je dosta jasna: ova potencija od za neparne. Motivacija za ovo je dosta jasna: ova potencija od  sjeionako uvijek ili sjeionako uvijek ili  ili ili  , pa idemo gledati te slučajeve odvojeno, kad već možemo. Također, vidimo da će nam ovo pomoći sa kosinusom u nazivniku. , pa idemo gledati te slučajeve odvojeno, kad već možemo. Također, vidimo da će nam ovo pomoći sa kosinusom u nazivniku.
Znamo (ponovno, sigurno ste rekli/dokazivali na vježbama, reci ako treba što objasniti) da vrijedi 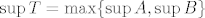 i i 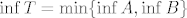 . Dakle, bit će nam dovoljno znati infimume i supremume ova dva manja skupa. . Dakle, bit će nam dovoljno znati infimume i supremume ova dva manja skupa.
Kod tih ulazi napokon i treća ideja koju ćemo spominjati. Naime, pogledajmo kako  izgleda. To je zapravo, kad se riješimo svih kerefeka, skup izgleda. To je zapravo, kad se riješimo svih kerefeka, skup 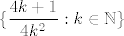 (tu smo uzimali (tu smo uzimali 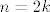 , čime "pokrivamo" točno sve parne prirodne , čime "pokrivamo" točno sve parne prirodne  ). ).
E, a za ovaj pripadajući niz (definiran s 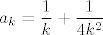 ) mi možemo reći da je padajuć. Naime, oba pribrojnika su mu padajuća. Stoga, (ponovno, po lako dokazivoj stvari koju ste sigurno radili na vježbama i koja je intuitivno dosta jasna), ) mi možemo reći da je padajuć. Naime, oba pribrojnika su mu padajuća. Stoga, (ponovno, po lako dokazivoj stvari koju ste sigurno radili na vježbama i koja je intuitivno dosta jasna), 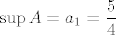 , a , a 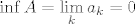 . .
Dobro, preostaje nam još jedino skup  . Ponovno, kad se riješimo kosinusa (jer znamo koliko je to kosinus od "neparno" pijeva), dobivamo da je . Ponovno, kad se riješimo kosinusa (jer znamo koliko je to kosinus od "neparno" pijeva), dobivamo da je 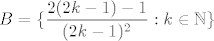 (tu uzimamo, s istom argumentacijom kao gore, (tu uzimamo, s istom argumentacijom kao gore, 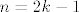 ). ).
E, dobro, tu će stvar biti malo ružnija nego u prvom skupu, ali i dalje rješiva. Dakle, tvrdimo da je i niz definiran s 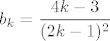 padajuć. Dokažimo to: direktno ćemo provjeriti vrijedi li uvijek padajuć. Dokažimo to: direktno ćemo provjeriti vrijedi li uvijek 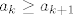 . To je očito ekvivalentno s . To je očito ekvivalentno s 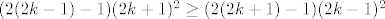 . E, sad, kad se to raspiše dobivamo (valjda . E, sad, kad se to raspiše dobivamo (valjda  ) da je to ekvivalentno s ) da je to ekvivalentno s 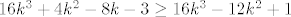 , tj. s , tj. s 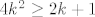 . To, naravno, očito vrijedi, što nam je valjda najlakše vidjeti (ili barem meni najlakše zapisati . To, naravno, očito vrijedi, što nam je valjda najlakše vidjeti (ili barem meni najlakše zapisati  ) ako prikažemo u obliku ) ako prikažemo u obliku 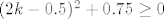 (kako god išla, indukcijom, direktnim rješavanjem kvadratne čime već, svejedno je... (kako god išla, indukcijom, direktnim rješavanjem kvadratne čime već, svejedno je...  ). ).
Stoga, koristeći istu argumentaciju kao za  , vrijedi , vrijedi 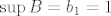 i i 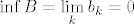 . .
Sad smo gotovi. Naime, onda znamo da je 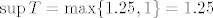 , a , a 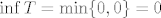 , pa je , pa je 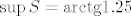 , a , a 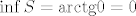 . .
Evo, i to bi bilo kao to. Mislim da su razlozi zašto neću pisati drugu grupu u ovom trenutku očiti. 
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 19:32 čet, 6. 1. 2011 Naslov: Postano: 19:32 čet, 6. 1. 2011 Naslov: |
    |
|
|
Kolega mornik me pretekao dok sam pisao ovo, ali srecom rijesili smo razlicite zadatke :D
Trebamo pronaci supremum i infimum skupa
[latex]S = \left\{ \sinh \left( \displaystyle\frac{(-1)^n + 2n}{n \sin\left( \frac{(-1)^{n-1}\pi}{2} \right)} \right) : n \in \mathbb{N} \right\}[/latex]
Prvo treba primjetiti da je sinus hiperbolni strogo rastuca funkcija na [latex]\mathbb{R}[/latex] pa je dovoljno pronaci supremum i infimum argumenta.
[latex]T := \left\{ \displaystyle\frac{(-1)^n + 2n}{n \sin\left( \frac{(-1)^{n-1}\pi}{2} \right)} : n \in \mathbb{N} \right\}[/latex]
Vrijedi: [latex]\sup S = \sinh (\sup T), \quad\inf S = \sinh (\inf T)[/latex]
Da nadjemo sup i inf skupa T, rastavit cemo T na uniju skupova takvu da su elementi skupova unije monotoni nizovi u [latex]\mathbb{R}[/latex] pa definiramo:
[latex]
T_{2k-1} := \left\{ \displaystyle\frac{(-1)^{2k-1} + 2(2k-1)}{(2k-1) \sin\left( \frac{(-1)^{(2k-1) - 1}\pi}{2} \right)} : k \in \mathbb{N} \right\} = \left\{ 2 - \displaystyle\frac{1}{2k-1} : k \in \mathbb{N}\right\}[/latex]
[latex]
T_{2k} := \left\{ \displaystyle\frac{(-1)^{2k} + 2\cdot 2k}{2k \sin\left( \frac{(-1)^{2k - 1}\pi}{2} \right)} : k \in \mathbb{N} \right\} = \left\{ -2 - \displaystyle\frac{1}{2k} : k\in\mathbb{N} \right\}[/latex]
Vrijedi: [latex]T_{2k-1} \displaystlye\cup T_{2k} = T \implies \sup T = \max \{\sup T_{2k-1}, \sup T_{2k}\}, \quad \inf T = \min \{\inf T_{2k-1}, \inf T_{2k}\}[/latex]
Sad definiramo nizove:
[latex]a_k := 2 - \displaystyle\frac{1}{2k-1} \\
b_k := -2 - \displaystyle\frac{1}{2k}, \quad k\in \mathbb{N}[/latex]
Ocito su oba niza rastuca pa je
[latex]\sup T_{2k-1} = \displaystyle\lim_{k \to\infty} a_k = 2, \quad \inf T_{2k-1} = a_1 = 1[/latex]
[latex]\sup T_{2k} = \displaystyle\lim_{k \to\infty} b_k = -2, \quad \inf T_{2k} = b_1 = -\displaystyle\frac{5}{2}[/latex]
[latex]\implies \boxed{ \sup S = \displaystyle\frac{e^2 - e^{-2}}{2}, \quad \inf S = \displaystyle\frac{e^{-\frac{5}{2}}-e^{\frac{5}{2}}}{2}}[/latex]
Kolega mornik me pretekao dok sam pisao ovo, ali srecom rijesili smo razlicite zadatke 
Trebamo pronaci supremum i infimum skupa
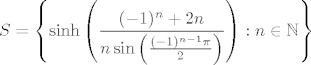
Prvo treba primjetiti da je sinus hiperbolni strogo rastuca funkcija na  pa je dovoljno pronaci supremum i infimum argumenta. pa je dovoljno pronaci supremum i infimum argumenta.
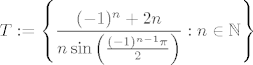
Vrijedi: 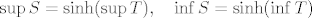
Da nadjemo sup i inf skupa T, rastavit cemo T na uniju skupova takvu da su elementi skupova unije monotoni nizovi u  pa definiramo: pa definiramo:
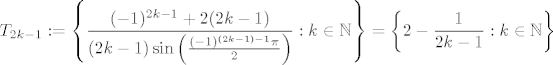
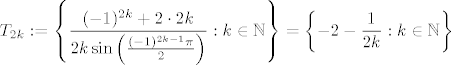
Vrijedi: 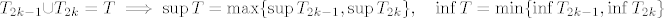
Sad definiramo nizove:
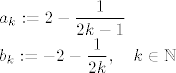
Ocito su oba niza rastuca pa je
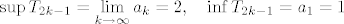
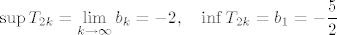

|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
 Postano: 21:09 čet, 6. 1. 2011 Naslov: Postano: 21:09 čet, 6. 1. 2011 Naslov: |
    |
|
|
http://web.math.hr/nastava/analiza/files/ma1-zadaca4.pdf
U 7. zadatku kada skup rastavimo na zbroj an+bn.
[latex]\displaystyle \frac{12 m - n - 3 m n + 7}{(m + 1)(5 - 2n)} = \frac{2 m + 1}{m + 1} + \frac{n + 2}{5 - 2 n}[/latex].
Kada bn gledamo kao funkciju, kao sto vidimo na grafu
http://www.wolframalpha.com/input/?i=y%3D+%28x%2B2%29%2F%285-2x%29+from+-1+to+10 na intevalu [0,5/2> je strogo rastuca i ide do beskonacnosti, a od <5/2,beskonacnosti>ide od -beskonacnosti do neke vrijednosti. Kako da tu nadem inf i sup? Da gledam od n≥3 ili...?
Hvala.
http://web.math.hr/nastava/analiza/files/infsup.pdf
Kako se dode do supremuma u 2. zadatku?
U 7. zadatku, mogla bih podijeliti skup na umnozak a_n*b_n.
supa_n=2 i infa_n=-2.
E sada kak naci omedenost b_n-a? Kak da ga rastavimo? Fiksirala sam n=1 i na acin gledala sup i inf, pa sam fiksirala m=1. Da rastavim na nekaj kaj slici parcijalnom razlomku? Na koji nacin?
http://web.math.hr/nastava/analiza/files/ma1-zadaca4.pdf
U 7. zadatku kada skup rastavimo na zbroj an+bn.
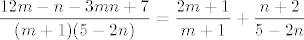 . .
Kada bn gledamo kao funkciju, kao sto vidimo na grafu
http://www.wolframalpha.com/input/?i=y%3D+%28x%2B2%29%2F%285-2x%29+from+-1+to+10 na intevalu [0,5/2> je strogo rastuca i ide do beskonacnosti, a od <5/2,beskonacnosti>ide od -beskonacnosti do neke vrijednosti. Kako da tu nadem inf i sup? Da gledam od n≥3 ili...?
Hvala.
http://web.math.hr/nastava/analiza/files/infsup.pdf
Kako se dode do supremuma u 2. zadatku?
U 7. zadatku, mogla bih podijeliti skup na umnozak a_n*b_n.
supa_n=2 i infa_n=-2.
E sada kak naci omedenost b_n-a? Kak da ga rastavimo? Fiksirala sam n=1 i na acin gledala sup i inf, pa sam fiksirala m=1. Da rastavim na nekaj kaj slici parcijalnom razlomku? Na koji nacin?
Zadnja promjena: A-tom; 0:13 pet, 7. 1. 2011; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 21:41 čet, 6. 1. 2011 Naslov: Postano: 21:41 čet, 6. 1. 2011 Naslov: |
    |
|
|
niz b_n je negativan za n>=3, tako da se supremum postiže kad je n=1 ili n=2.
Kad trazimo inf, opet ocito je da ne gledamo n=1, niti n=2, nego n>=3. A posto je funkcija strogo rastuca za n>=3, inf je za n=3.
niz b_n je negativan za n>=3, tako da se supremum postiže kad je n=1 ili n=2.
Kad trazimo inf, opet ocito je da ne gledamo n=1, niti n=2, nego n>=3. A posto je funkcija strogo rastuca za n>=3, inf je za n=3.
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 3:58 pet, 7. 1. 2011 Naslov: Postano: 3:58 pet, 7. 1. 2011 Naslov: |
    |
|
|
@A-tom
2. zadatak:
zadatak je malo petljaviji, ali nista strasno
Izraz [latex]\left\lfloor \sqrt[|n|]{\displaystyle\frac{7}{3}}\right\rfloor[/latex] ce poprimiti vrijednost 1 za [latex]|n| \geq 2[/latex], a za [latex]n \in \{-1,1\}[/latex] ce poprimiti vrijednost 2.
Neka je [latex]f(n) = \left\lfloor \sqrt[|n|]{\displaystyle\frac{7}{3}}\right\rfloor \cdot \displaystyle\frac{n^2 - 2n -4}{n^2 - n -6}[/latex].
Za [latex]n > 3[/latex] imamo:
[latex]f(n + 3) = 1 - \displaystyle\frac{n+1}{n(n+5)} < 1, \forall n\in\mathbb{N}[/latex]
Za [latex]n \leq -3[/latex] imamo:
[latex]f(- n - 2) = \displaystyle\frac{n^2 + 6n +4}{n^2 + 5n}, n \in\mathbb{N}[/latex]
Lako se provjeri da je [latex](f(-n-2))_{n\in\mathbb{N}}[/latex] padajuc niz pa se supremum postize u [latex]f(-3) = \frac{11}{6}[/latex].
Sad nam samo preostaje provjeriti [latex]f(-1) = \frac{1}{2}, f(1) = \frac{5}{3}, f(2) = 1[/latex]
Slijedi da je supremum skupa [latex]\boxed{\displaystyle\frac{11}{6}}[/latex].
7. zadatak:
Ja cu dati svoje rjesenje u kratkim crtama buduci da niti znam sto kako oznacavas, niti sam dobio brojke kao ti :)
[latex]S = \left\{ \cos (m^2\pi)\cdot\displaystyle\frac{2-3m}{m+1}\cdot\cos (n\pi)\cdot\displaystyle\frac{n+1}{n} : m,n \in \mathbb{N} \right\}[/latex]
Neka su
[latex]A = \left\{ \cos (m^2\pi)\cdot\displaystyle\frac{2-3m}{m+1} : m\in\mathbb{N} \right\}[/latex]
[latex]B = \left\{ \cos (n\pi)\cdot\displaystyle\frac{n+1}{n} : n\in\mathbb{N} \right\}[/latex]
[latex]A\cdot B := \{ xy : x\in A, y\in B\} = S[/latex]
[latex]
A = \left\{ \cos (4k^2\pi) \cdot\displaystyle\frac{2-6k}{2k+1} :k \in\mathbb{N} \right\} \cup \left\{ \cos (4k^2\pi - 4k\pi +\pi) \cdot\displaystyle\frac{5-6k}{2k}\right\} \\ = \left\{ -3 + \displaystyle\frac{5}{2k+1} : k\in\mathbb{N} \right\} \cup \left\{ 3 - \displaystyle\frac{5}{2k} :k\in\mathbb{N} \right\} \implies \sup A = 3, \quad\inf A = -3[/latex]
[latex]B = \left\{ \cos (2k\pi)\cdot \displaystyle\frac{2k+1}{2k}:k\in\mathbb{N} \right\} \cup \left\{ \cos (2k-1)\pi \cdot \displaystyle\frac{2k}{2k-1}:k\in\mathbb{N} \right\} \\ = \left\{ 1 + \displaystyle\frac{1}{2k} :k\in\mathbb{N}\right\} \cup \left\{ -1 - \displaystlye\frac{1}{2k-1}:k\in\mathbb{N} \right\} \implies \sup B = \displaystlye\frac{3}{2}, \quad\inf B = -2[/latex]
Sad vidimo da je [latex]\boxed{\sup S = 6,\quad \inf S = -6}[/latex]
@A-tom
2. zadatak:
zadatak je malo petljaviji, ali nista strasno
Izraz 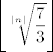 ce poprimiti vrijednost 1 za ce poprimiti vrijednost 1 za 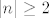 , a za , a za 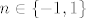 ce poprimiti vrijednost 2. ce poprimiti vrijednost 2.
Neka je 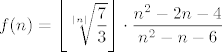 . .
Za 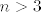 imamo: imamo:
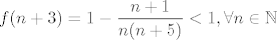
Za 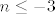 imamo: imamo:
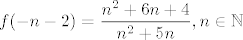
Lako se provjeri da je  padajuc niz pa se supremum postize u padajuc niz pa se supremum postize u 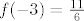 . .
Sad nam samo preostaje provjeriti 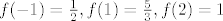
Slijedi da je supremum skupa 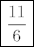 . .
7. zadatak:
Ja cu dati svoje rjesenje u kratkim crtama buduci da niti znam sto kako oznacavas, niti sam dobio brojke kao ti 
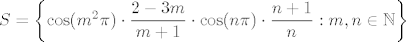
Neka su
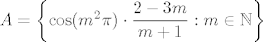
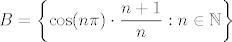
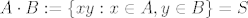
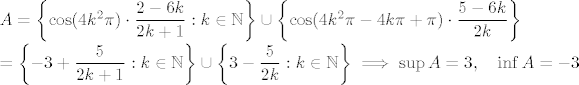
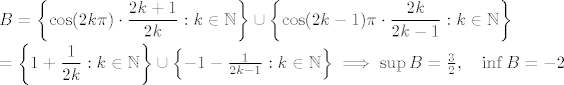
Sad vidimo da je 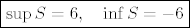
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
 Postano: 11:39 pet, 7. 1. 2011 Naslov: Postano: 11:39 pet, 7. 1. 2011 Naslov: |
    |
|
|
@Flame
Odlicno, hvala! Generalno nemam roblema s takvim zadatcima, tj. racunanjem i unijom, itd. Najveci problem je kako od onakve kobase to reducirati na "ljepsi" niz. Ja sam to isla racunati tako da je zagrada s cos a_n, a b_n je razlomak s m i n. inf i sup od cos je lagano izracunati, a za m i n sam fiksirala jednu vrijednost i setala se nizom, ali ne bas uspjesno :S
Mozes li molim te raspisati kako si reducirao S do umnoska dva cosinusa?
Nadalje imas li neki savjet ili caku kako se to elegenatno napravi?
Jos jedanput, velika hvala na pomoci!
@Flame
Odlicno, hvala! Generalno nemam roblema s takvim zadatcima, tj. racunanjem i unijom, itd. Najveci problem je kako od onakve kobase to reducirati na "ljepsi" niz. Ja sam to isla racunati tako da je zagrada s cos a_n, a b_n je razlomak s m i n. inf i sup od cos je lagano izracunati, a za m i n sam fiksirala jednu vrijednost i setala se nizom, ali ne bas uspjesno :S
Mozes li molim te raspisati kako si reducirao S do umnoska dva cosinusa?
Nadalje imas li neki savjet ili caku kako se to elegenatno napravi?
Jos jedanput, velika hvala na pomoci!
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Ivanaa
Forumaš(ica)
Pridružen/a: 18. 10. 2010. (22:26:06)
Postovi: (35)16
|
|
| [Vrh] |
|
|















