| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:11 pet, 10. 12. 2010 Naslov: Re: 3. zadaća Postano: 19:11 pet, 10. 12. 2010 Naslov: Re: 3. zadaća |
    |
|
|
[quote="medonja"]Zad. 8 pod b) - jel mogu prvo razdvojit na 2 limesa(Po tm 2.4. 3. iz skripte) i onda ta 2 limesa razdvojit isto po tm 2.4.1.? jel to onda ok rjesenje?[/quote]
Sorry, ne da mi se sad tražiti ta skripta. Prvo što mi pada na pamet je rješiti taj zadatak ovako: [latex]\displaystyle \lim_{n \to \infty} \frac{1 + \sqrt[4]{n}}{5 + \sqrt[3]{n}} : \frac{\sqrt[3]{n}}{\sqrt[3]{n}} = \lim_{n \to \infty} \frac{\frac{1}{\sqrt[3]{n}} + \frac{1}{\sqrt[12]{n}}}{\frac{5}{\sqrt[3]{n}} + 1} = \frac{0 + 0}{0 + 1} = 0[/latex]
[quote="medonja"]Molila bih kolege koji su rješili ako imaju vrem da napišu rješenja i objašnjenja od zadataka- 2.(c), 9.(c), 12.(c), 15.(c) i 16.(d).[/quote]
2.(c) [url=http://degiorgi.math.hr/forum/viewtopic.php?p=129226&highlight=\\frac{1}{\\arctan(-n)}#129226]Ovdje[/url] je to mornik lijepo objasnio.
9.(c) Teorem o sendviču. Iskoristi [latex]-1 \leq \cos n \leq 1[/latex].
12.(c) Pojavljuju se eksponencijalne funkcije. Prirodno je promatrati slučajeve [latex]|x| < 1[/latex], [latex]|x| = 1[/latex] i [latex]|x| > 1[/latex].
15.(c) [latex]\displaystyle \sum_{k = 1}^n k (k + 1) = \sum_{k = 1}^n (k^2 + k) = \sum_{k = 1}^n k^2 + \sum_{k = 1}^n k[/latex]. Svaku od tih suma bi trebala znati.
16.(d) Vrijedi [latex]\displaystyle \sum_{k = 1}^n k^3 = \frac{n^2 (n + 1)^2}{4}[/latex]. Može se dokazati indukcijom. Formula se može izvesti metodom zvanom teleskopiranje.
U 15.(c) i 16.(d) se može iskoristiti i Stolzov teorem.
| medonja (napisa): | | Zad. 8 pod b) - jel mogu prvo razdvojit na 2 limesa(Po tm 2.4. 3. iz skripte) i onda ta 2 limesa razdvojit isto po tm 2.4.1.? jel to onda ok rjesenje? |
Sorry, ne da mi se sad tražiti ta skripta. Prvo što mi pada na pamet je rješiti taj zadatak ovako: 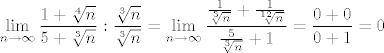
| medonja (napisa): | | Molila bih kolege koji su rješili ako imaju vrem da napišu rješenja i objašnjenja od zadataka- 2.(c), 9.(c), 12.(c), 15.(c) i 16.(d). |
2.(c) Ovdje je to mornik lijepo objasnio.
9.(c) Teorem o sendviču. Iskoristi 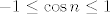 . .
12.(c) Pojavljuju se eksponencijalne funkcije. Prirodno je promatrati slučajeve  , , 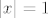 i i  . .
15.(c) 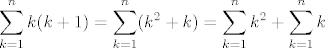 . Svaku od tih suma bi trebala znati. . Svaku od tih suma bi trebala znati.
16.(d) Vrijedi 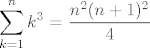 . Može se dokazati indukcijom. Formula se može izvesti metodom zvanom teleskopiranje. . Može se dokazati indukcijom. Formula se može izvesti metodom zvanom teleskopiranje.
U 15.(c) i 16.(d) se može iskoristiti i Stolzov teorem.
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 15:21 sub, 11. 12. 2010 Naslov: Postano: 15:21 sub, 11. 12. 2010 Naslov: |
    |
|
|
[quote="medonja"]Ovaj 8 b)..mislim odma se vidi da mu je limes 0, al kak si dijelio sa dva različita n? Mislim jedino ak sam ja čorava- u brojnik si stavio 3 korjen iz n, a u nazivnik 5.korjen od n???[/quote]
Piše 3, samo je taj latex mutan. Čak ni sa Ctrl+ nije jasnije.
Ako znaš čitati latex kod, možeš ga pročitati tako da staviš kursor na zelenog smajlija gore desno. :)
[quote="medonja"]I,da - teskopiranje?! To je...? :oops:[/quote]
Jednostavno rečeno, to je kad puno toga zbrojiš, pa se onda većina toga skrati. Sjećam se da smo radili tu fintu na vježbama, pa sam mislio da nisi prvi put čula za to.
No, ajmo izvesti [latex]\displaystyle \sum_{k = 1}^n k^3 = \frac{n^2 (n + 1)^2}{4}[/latex]. Uočimo da je [latex](k + 1)^4 - k^4 = 4 k^3 + 6 k^2 + 4 k + 1[/latex]. Sumirajmo to za sve [latex]k[/latex] td. [latex]1 \leq k \leq n[/latex]. Dobivamo
[latex]\displaystyle $\begin{align*}
\sum_{k = 1}^n \left( (k + 1)^4 - k^4 \right) & = \sum_{k = 1}^n \left( 4 k^3 + 6 k^2 + 4 k + 1 \right) \\
(n + 1)^4 - 1^4 & = 4 \sum_{k = 1}^n k^3 + 6 \sum_{k = 1}^n k^2 + 4 \sum_{k = 1}^n k + \sum_{k = 1}^n 1 \\
(n + 1)^4 - 1 & = 4 \sum_{k = 1}^n k^3 + 6 \cdot \frac{n (n + 1) (2 n + 1)}{6} + 4 \cdot \frac{n (n + 1)}{2} + n \\
4 \sum_{k = 1}^n k^3 & = (n + 1)^4 - n (n + 1) (2 n + 1) - 2 n (n + 1) - (n + 1) \\
4 \sum_{k = 1}^n k^3 & = (n + 1) \left[ (n + 1)^3 - n (2 n + 1) - 2 n - 1\right] \\
4 \sum_{k = 1}^n k^3 & = (n + 1) \left[ (n + 1)^3 - (2 n + 1)(n + 1) \right] \\
4 \sum_{k = 1}^n k^3 & = (n + 1)^2 \left[ (n + 1)^2 - (2 n + 1) \right] \\
\sum_{k = 1}^n k^3 & = \frac{n^2 (n + 1)^2}{4}
\end{align*}$[/latex]
Onaj maštoviti dio zvani teleskopiranje se zbio na lijevoj strani jednakosti kod prijelaza iz prvog u drugi redak. Sve ostalo je tehnički izvod.
Primijeti da smo morali iskoristiti sve sume s manjim potencijama, tako da ova metoda nije baš najefikasnija za veće potencije. Srećom, postoje još barem tri metode koje ne funkcioniraju tako.
| medonja (napisa): | | Ovaj 8 b)..mislim odma se vidi da mu je limes 0, al kak si dijelio sa dva različita n? Mislim jedino ak sam ja čorava- u brojnik si stavio 3 korjen iz n, a u nazivnik 5.korjen od n??? |
Piše 3, samo je taj latex mutan. Čak ni sa Ctrl+ nije jasnije.
Ako znaš čitati latex kod, možeš ga pročitati tako da staviš kursor na zelenog smajlija gore desno. 
| medonja (napisa): | I,da - teskopiranje?! To je...?  |
Jednostavno rečeno, to je kad puno toga zbrojiš, pa se onda većina toga skrati. Sjećam se da smo radili tu fintu na vježbama, pa sam mislio da nisi prvi put čula za to.
No, ajmo izvesti 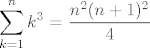 . Uočimo da je . Uočimo da je 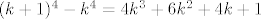 . Sumirajmo to za sve . Sumirajmo to za sve  td. td. 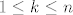 . Dobivamo . Dobivamo
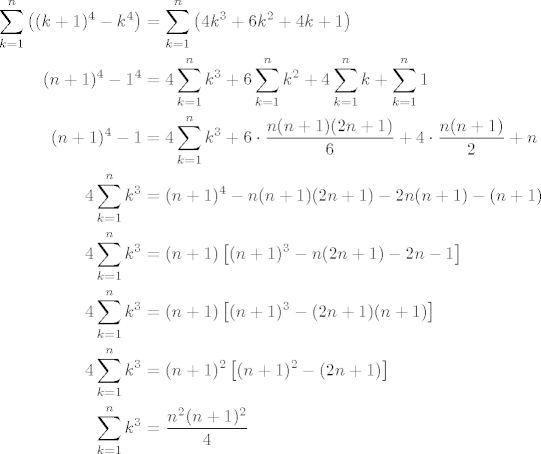
Onaj maštoviti dio zvani teleskopiranje se zbio na lijevoj strani jednakosti kod prijelaza iz prvog u drugi redak. Sve ostalo je tehnički izvod.
Primijeti da smo morali iskoristiti sve sume s manjim potencijama, tako da ova metoda nije baš najefikasnija za veće potencije. Srećom, postoje još barem tri metode koje ne funkcioniraju tako.
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 13:03 uto, 14. 12. 2010 Naslov: Postano: 13:03 uto, 14. 12. 2010 Naslov: |
    |
|
|
Mislim, ja ovo, formalno rečeno, jesam riješio (mislim da ti je dobro... ima nešto s korijenima iz [latex]2[/latex] u rješenju :D), ali nažalost ne mogu u ovome trenutku opravdati sve dijelove dokaza. :( Stoga ću tu napisati cijelo "rješenje", ali imaj na umu da stvar nije potpuna. Pogledat ću još mogu li negdje biti pametan, vuče me na to da postoji neko kombinatorno objašnjenje, ali eto.
Dakle, način na koji sam ja išao (ne jamčim da ne postoji bolji... dapače, začudio bih se da ne postoji :D): očito vrijedi [latex]a_{n+1}-a_n=\displaystyle\frac{1-2n}{2n}(a_n-a_{n-1})[/latex]. Teleskopiranjem, indukcijom ili kako već dolazimo lako do toga da je [latex]a_{n+1}-a_n=\displaystyle\frac{(1-2n)(3-2n)\cdots 3}{(2n)(2n-2)\cdots 4}(b-a)=\displaystyle\frac{2\cdot (-1)^{n-1}(2n-1)!!}{(2n)!!}[/latex]. (U ovom zapisu, [latex]k!!:=k\cdot (k-2)\cdot (k-4)\cdots[/latex], pri čemu je zadnji član u produktu [latex]2[/latex] ili [latex]1[/latex], ovisno o parnosti [latex]k[/latex]). Označimo, čisto radi lakšeg zapisa, s [latex]T(n)=\displaystyle\frac{2\cdot (-1)^n(2n+1)!!}{(2n+2)!!}[/latex].
E, sad, dolazi ovaj dio za koji baš i nemam objašnjenje. Kažem, moguće je da [latex]T_n[/latex] u sebi ima neki kombinatorni element, ali trenutno ga ne vidim. Nisam neko dulje vrijeme potrošio na ovo, pa je moguće da je očito, doduše.
U svakom slučaju, očito je dakle [latex]a_{n+1}=T(n-1)(b-a)+a_n=(T(n-1)+T(n-2))(b-a)+a_{n-1}[/latex]. Nastavljamo dalje, formalno indukcijom ili kako već, i dobivamo da je [latex]a_{n+1}=(T(n-1)+T(n-2)+\ldots+T(2)+T(1))(b-a)+a_2=(b-a)\displaystyle\sum_{i=1}^{n-1}T(i)+b[/latex].
No, sada ispada da je, iz meni trenutno nepoznatih razloga (iako je WolframAlpha uz minimalnu modifikaciju izbacila točan, simbolički, rezultat, pa pretpostavljam da se radi o nekoj verziji poznatog limesa koji možda ima, a možda nema veze s tzv. hipergeometrijskim funkcijama), [latex]\displaystyle\lim_{n}\sum_{i=1}^{n-1}T(i)=1-\sqrt{2}[/latex].
Stoga, ispada da je [latex]\displaystyle\lim_{n}a_n=(1-\sqrt{2})(b-a)+b=(2-\sqrt{2})b+(\sqrt{2}-1)a[/latex], baš kako si rekao. :)
Kažem, ja sam razumno uvjeren da je ovaj rezultat točan, ali u ovom trenutku ne mogu reći zašto je suma reda [latex]\sum T(n)[/latex] jednaka baš [latex]1-\sqrt{2}[/latex]. Ovaj prvi dio s gledanjem razlika susjednih članova niza mi se čini relativno bitnim za rješavanje ali, kažem, moguće, pa čak i vjerojatno, je da ima i boljih rješenja. :)
Mislim, ja ovo, formalno rečeno, jesam riješio (mislim da ti je dobro... ima nešto s korijenima iz  u rješenju u rješenju  ), ali nažalost ne mogu u ovome trenutku opravdati sve dijelove dokaza. ), ali nažalost ne mogu u ovome trenutku opravdati sve dijelove dokaza.  Stoga ću tu napisati cijelo "rješenje", ali imaj na umu da stvar nije potpuna. Pogledat ću još mogu li negdje biti pametan, vuče me na to da postoji neko kombinatorno objašnjenje, ali eto. Stoga ću tu napisati cijelo "rješenje", ali imaj na umu da stvar nije potpuna. Pogledat ću još mogu li negdje biti pametan, vuče me na to da postoji neko kombinatorno objašnjenje, ali eto.
Dakle, način na koji sam ja išao (ne jamčim da ne postoji bolji... dapače, začudio bih se da ne postoji  ): očito vrijedi ): očito vrijedi 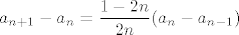 . Teleskopiranjem, indukcijom ili kako već dolazimo lako do toga da je . Teleskopiranjem, indukcijom ili kako već dolazimo lako do toga da je 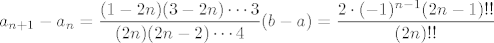 . (U ovom zapisu, . (U ovom zapisu, 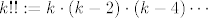 , pri čemu je zadnji član u produktu , pri čemu je zadnji član u produktu  ili ili  , ovisno o parnosti , ovisno o parnosti  ). Označimo, čisto radi lakšeg zapisa, s ). Označimo, čisto radi lakšeg zapisa, s 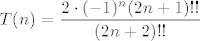 . .
E, sad, dolazi ovaj dio za koji baš i nemam objašnjenje. Kažem, moguće je da 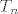 u sebi ima neki kombinatorni element, ali trenutno ga ne vidim. Nisam neko dulje vrijeme potrošio na ovo, pa je moguće da je očito, doduše. u sebi ima neki kombinatorni element, ali trenutno ga ne vidim. Nisam neko dulje vrijeme potrošio na ovo, pa je moguće da je očito, doduše.
U svakom slučaju, očito je dakle 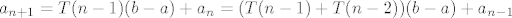 . Nastavljamo dalje, formalno indukcijom ili kako već, i dobivamo da je . Nastavljamo dalje, formalno indukcijom ili kako već, i dobivamo da je 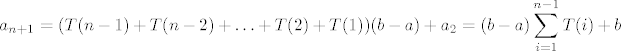 . .
No, sada ispada da je, iz meni trenutno nepoznatih razloga (iako je WolframAlpha uz minimalnu modifikaciju izbacila točan, simbolički, rezultat, pa pretpostavljam da se radi o nekoj verziji poznatog limesa koji možda ima, a možda nema veze s tzv. hipergeometrijskim funkcijama), 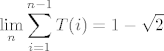 . .
Stoga, ispada da je 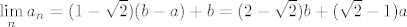 , baš kako si rekao. , baš kako si rekao. 
Kažem, ja sam razumno uvjeren da je ovaj rezultat točan, ali u ovom trenutku ne mogu reći zašto je suma reda 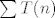 jednaka baš jednaka baš 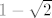 . Ovaj prvi dio s gledanjem razlika susjednih članova niza mi se čini relativno bitnim za rješavanje ali, kažem, moguće, pa čak i vjerojatno, je da ima i boljih rješenja. . Ovaj prvi dio s gledanjem razlika susjednih članova niza mi se čini relativno bitnim za rješavanje ali, kažem, moguće, pa čak i vjerojatno, je da ima i boljih rješenja. 
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
|










