Za jedan način trebaš napraviti sve moguće grupacije istih prostih faktora; npr. za n = 200 je rastav napisan bez potencija 2x2x2x5x5, pa prvo uzimaš Z/2Z + Z/2Z + Z/2Z + Z/5Z + Z/5Z (gdje je svakom prostom faktoru "pridružena" jedna grupa), pa onda Z/2Z + Z/4Z + Z/5Z + Z5/Z (gdje grupiraš dvije dvojke), pa Z/8Z + Z/5Z + Z/5Z, pa onda opet iste ove tri mogućnosti s dvojkama, samo sada sa Z/25Z u sumi umjesto Z/5Z + Z/5Z.
Za drugi način, u kojem se grupa prikazuje kao suma konačnih cikličkih grupa takvih da red prethodne uvijek dijeli red sljedeće, uzimaš jednu po jednu grupu zapisanu na prvi način i kao zadnji član direktne sume u njenom drugom prikazu pišeš Z/(produkt najviših potencija svih uključenih prostih faktora)Z, i zatim postupak ponajvljaš za predzadnji itd. (dakle iskorištavaš činjenicu da je [latex]\mathbb Z/m \mathbb Z \oplus \mathbb Z/n \mathbb Z \cong \mathbb Z/(mn) \mathbb Z[/latex] za (i samo za :)) relativno proste m i n), jer upravo tako dobivaš brojeve rastući sortirane po djeljivosti.
npr. [latex]\mathbb Z/2\mathbb Z \oplus \mathbb Z/2\mathbb Z \oplus \mathbb Z/2\mathbb Z \oplus \mathbb Z/5\mathbb Z \oplus \mathbb Z/5\mathbb Z \cong[/latex] (prosti faktori s kojima radimo su 2 i 5, a ovdje su upravo 2 i 5 njihove najviše potencije) [latex]\cong (\mathbb Z/2\mathbb Z \oplus \mathbb Z/2\mathbb Z \oplus \mathbb Z/5\mathbb Z) \oplus \mathbb Z/(2\cdot5)\mathbb Z \cong (\mathbb Z/2\mathbb Z) \oplus \mathbb Z/(2\cdot5)\mathbb Z \oplus \mathbb Z/10\mathbb Z \cong[/latex] (sada ostaju samo dvojke, ili je, ako hoćeš, najviša potencija petice 5^0 :)) [latex]\cong \mathbb Z/2\mathbb Z \oplus \mathbb Z/10\mathbb Z \oplus \mathbb Z/10\mathbb Z[/latex]
Ili npr. pretvorba jednoga prikaza jedne od Abelovih grupa reda 12000 u drugi :D
[latex]\mathbb Z/2\mathbb Z \oplus \mathbb Z/2\mathbb Z \oplus \mathbb Z/2^3\mathbb Z \oplus \mathbb Z/3\mathbb Z \oplus \mathbb Z/5\mathbb Z \oplus \mathbb Z/5^2\mathbb Z \cong (\mathbb Z/2\mathbb Z \oplus \mathbb Z/2\mathbb Z \oplus \mathbb Z/5\mathbb Z) \oplus \mathbb Z/(2^3\cdot3\cdot5^2)\mathbb Z \cong (\mathbb Z/2\mathbb Z) \oplus \mathbb Z/(2\cdot5)\mathbb Z \oplus \mathbb Z/600\mathbb Z \cong \mathbb Z/2\mathbb Z \oplus \mathbb Z/10\mathbb Z \oplus \mathbb Z/600\mathbb Z [/latex]
Nadam se da je jasno, postupci su zapravo vrlo jednostavno, samo što ih je malo teže (well, bar meni) opisati preko posta na forumu :)
Za jedan način trebaš napraviti sve moguće grupacije istih prostih faktora; npr. za n = 200 je rastav napisan bez potencija 2x2x2x5x5, pa prvo uzimaš Z/2Z + Z/2Z + Z/2Z + Z/5Z + Z/5Z (gdje je svakom prostom faktoru "pridružena" jedna grupa), pa onda Z/2Z + Z/4Z + Z/5Z + Z5/Z (gdje grupiraš dvije dvojke), pa Z/8Z + Z/5Z + Z/5Z, pa onda opet iste ove tri mogućnosti s dvojkama, samo sada sa Z/25Z u sumi umjesto Z/5Z + Z/5Z.
Za drugi način, u kojem se grupa prikazuje kao suma konačnih cikličkih grupa takvih da red prethodne uvijek dijeli red sljedeće, uzimaš jednu po jednu grupu zapisanu na prvi način i kao zadnji član direktne sume u njenom drugom prikazu pišeš Z/(produkt najviših potencija svih uključenih prostih faktora)Z, i zatim postupak ponajvljaš za predzadnji itd. (dakle iskorištavaš činjenicu da je 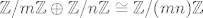 za (i samo za
za (i samo za  ) relativno proste m i n), jer upravo tako dobivaš brojeve rastući sortirane po djeljivosti.
) relativno proste m i n), jer upravo tako dobivaš brojeve rastući sortirane po djeljivosti.
npr. 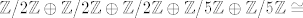 (prosti faktori s kojima radimo su 2 i 5, a ovdje su upravo 2 i 5 njihove najviše potencije)
(prosti faktori s kojima radimo su 2 i 5, a ovdje su upravo 2 i 5 njihove najviše potencije) 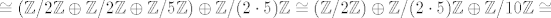 (sada ostaju samo dvojke, ili je, ako hoćeš, najviša potencija petice 5^0
(sada ostaju samo dvojke, ili je, ako hoćeš, najviša potencija petice 5^0  )
) 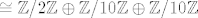
Ili npr. pretvorba jednoga prikaza jedne od Abelovih grupa reda 12000 u drugi 
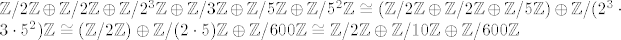
Nadam se da je jasno, postupci su zapravo vrlo jednostavno, samo što ih je malo teže (well, bar meni) opisati preko posta na forumu 
_________________
The lyf so short, the craft so long to lerne





