| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 0:29 sub, 6. 8. 2011 Naslov: Postano: 0:29 sub, 6. 8. 2011 Naslov: |
    |
|
|
1.
Sigurno vrijedi [latex]a_1, a_2 \neq 0[/latex] jer ako jedna jednadzba ima kompleksene korijene, onda joj je koeficijent uz [latex]x^2[/latex] razlicit od 0 jer su polinomi iz [latex]\mathbb{R}[x][/latex], a onda jer korijeni druge jednadzbe trebaju biti razliciti realni brojevi, vrijedi i da je i koeficijent uz [latex]x^2[/latex] druge jednadzbe razlicit od 0.
Iz toga slijedi da dane polinome mozemo normirati, pa jednadzbe postaju redom:
[latex]x^2 +2 \lambda _1 x + \mu _1 = 0, \quad x^2 + 2 \lambda _2 x + \mu _2 = 0 [/latex]
odnosno [latex]a_1a_2-2b_2b_2+c_1c_2=0[/latex] postaje
[latex]1 - 2 \lambda _1 \lambda _2 + \mu _1 \mu _2 = 0 \qquad (*)[/latex]
Bez smanjenja opcenitosti, pretpostavimo da prva jednadzba ima kompleksne korijene. To znači da joj je diskriminanta negativna, odnosno [latex]\lambda _1 ^2 < \mu _1[/latex] (primjetimo da nam to znači da je uvijek [latex]\mu _1> 0[/latex]).
Trebamo pokazati da je onda diskriminanta druge pozitivna (razliciti realni korijeni), odnosno [latex]\lambda _2 ^2 > \mu _2[/latex].
Neka je [latex] \lambda _1 = 0[/latex].
Slijedi [latex] \mu _1 > 0 [/latex] što uz [latex](*)[/latex] daje [latex] \mu _2 < 0 [/latex] pa trivijalno vrijedi [latex]\lambda _2 ^2 > \mu _2[/latex].
Neka je sad [latex] \lambda _1 \neq 0[/latex].
Vrijedi:
[latex]\lambda _1 ^2 < \mu _1 \implies \displaystyle\frac{1}{\lambda _1 ^2} > \displaystyle\frac{1}{\mu _1}[/latex].
Nadalje, [latex]\lambda _2 ^2 > \mu _2 \Leftrightarrow \displaystyle\frac{(1+\mu _1 \mu _2)^2}{4\lambda _1 ^2} > \mu _2[/latex]
[latex]\displaystyle\frac{1}{\lambda _1 ^2} > \displaystyle\frac{1}{\mu _1} \implies \displaystyle\frac{(1+\mu _1 \mu _2)^2}{4\lambda _1 ^2} > \displaystyle\frac{(1+\mu _1 \mu _2)^2}{4\mu _1} \geq \mu _2 \Leftrightarrow (1+\mu _1 \mu _2)^2 \geq 4\mu _1 \mu _2 \Leftrightarrow (1-\mu _1 \mu _2)^2 \geq 0 [/latex]
cime je tvrdnja dokazana.
2.
Neka je [latex]a \in \mathbb{C} \setminus \mathbb{Z}[/latex] zajednicki korijen danih jednadzbi. Dakle, [latex]a^2 + p_1 a + q_1 = 0[/latex] i [latex]a^2 + p_2 a + q_2 = 0 \implies (p_1 - p_2)a + (q_1 - q_2)=0[/latex].
Pretpostavimo da je [latex]p_1 \neq p_2[/latex]. Slijedi da je [latex]a = \displaystyle\frac{q_2 - q_1}{p_1 - p_2}[/latex]. Neka je [latex]M(q_2 - q_1, p_1 - p_2) = d[/latex], pa imamo [latex]a = \displaystyle\frac{\frac{q_2 - q_1}{d}}{\frac{p_1 - p_2}{d}}[/latex]. Buduci da su [latex] \frac{q_2 - q_1}{d}[/latex] i [latex]\frac{p_1 - p_2}{d}[/latex] relativno prosti, iz teorema o racionalnim korijenima polinoma [latex]\mathbb{Z}[x][/latex] slijedi da [latex]\frac{p_1 - p_2}{d} | 1 \implies p_1 - p_2 = \pm d \implies p_1 - p_2 | q_2 - q_1 \implies a \in \mathbb{Z}[/latex] sto je kontradikcija s pretpostavkom. Dakle [latex]p_1 = p_2 \implies q_1 = q_2[/latex].
1.
Sigurno vrijedi 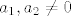 jer ako jedna jednadzba ima kompleksene korijene, onda joj je koeficijent uz jer ako jedna jednadzba ima kompleksene korijene, onda joj je koeficijent uz 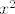 razlicit od 0 jer su polinomi iz razlicit od 0 jer su polinomi iz 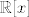 , a onda jer korijeni druge jednadzbe trebaju biti razliciti realni brojevi, vrijedi i da je i koeficijent uz , a onda jer korijeni druge jednadzbe trebaju biti razliciti realni brojevi, vrijedi i da je i koeficijent uz 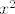 druge jednadzbe razlicit od 0. druge jednadzbe razlicit od 0.
Iz toga slijedi da dane polinome mozemo normirati, pa jednadzbe postaju redom:

odnosno 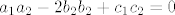 postaje postaje
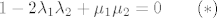
Bez smanjenja opcenitosti, pretpostavimo da prva jednadzba ima kompleksne korijene. To znači da joj je diskriminanta negativna, odnosno 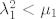 (primjetimo da nam to znači da je uvijek (primjetimo da nam to znači da je uvijek 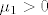 ). ).
Trebamo pokazati da je onda diskriminanta druge pozitivna (razliciti realni korijeni), odnosno 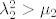 . .
Neka je 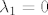 . .
Slijedi 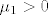 što uz što uz  daje daje 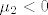 pa trivijalno vrijedi pa trivijalno vrijedi 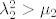 . .
Neka je sad 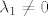 . .
Vrijedi:
 . .
Nadalje, 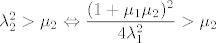
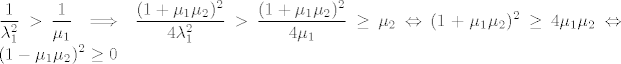
cime je tvrdnja dokazana.
2.
Neka je 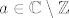 zajednicki korijen danih jednadzbi. Dakle, zajednicki korijen danih jednadzbi. Dakle, 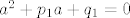 i i 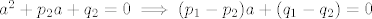 . .
Pretpostavimo da je 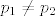 . Slijedi da je . Slijedi da je 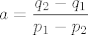 . Neka je . Neka je 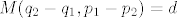 , pa imamo , pa imamo 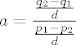 . Buduci da su . Buduci da su 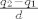 i i 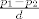 relativno prosti, iz teorema o racionalnim korijenima polinoma relativno prosti, iz teorema o racionalnim korijenima polinoma 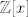 slijedi da slijedi da 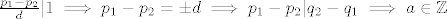 sto je kontradikcija s pretpostavkom. Dakle sto je kontradikcija s pretpostavkom. Dakle  . .
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
tihana
Forumaš(ica)


Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
 Postano: 6:04 sri, 17. 8. 2011 Naslov: Postano: 6:04 sri, 17. 8. 2011 Naslov: |
    |
|
|
Hvala na odgovorima imam jos dva zadatka za rjesit.
1.Nadji sve cijele brojeve [latex]p[/latex] tako da jednadzba [latex]px^2+(2p-1)x+p-2[/latex] ima racinalna rjesenja.Ja sam mislio ovako da pocne,mora da vazi [latex]x_1 x_2 \ge 0 \Rightarrow \frac{c}{a} \ge 0 \Rightarrow \frac{p-2}{p} \ge 0[/latex] iz ceka dobijem da je [latex]p \in (- \infty,0] \cup [2,\infty)[/latex] i [latex]x_1+x_2 \ge 0 \Rightarrow 0 \le p \le \frac{1}{2}[/latex],I nemam pojma kako da nastavim.
2.Neka su [latex]x_1[/latex] i [latex]x_2[/latex] realna rjesenja jednadzbe [latex]ax^2+bx+c=0 (a,b,c, \in R)[/latex] i vazi [latex]ax_1+bx_2+c=0[/latex].Dokazi da je: a)[latex]x_1=x_2^2[/latex] b) [latex]\sqrt [3]{ac^2}+\sqrt [3]{a^2c}+b=0[/latex].
Hvala na odgovorima imam jos dva zadatka za rjesit.
1.Nadji sve cijele brojeve  tako da jednadzba tako da jednadzba 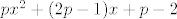 ima racinalna rjesenja.Ja sam mislio ovako da pocne,mora da vazi ima racinalna rjesenja.Ja sam mislio ovako da pocne,mora da vazi 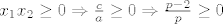 iz ceka dobijem da je iz ceka dobijem da je 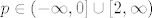 i i 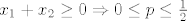 ,I nemam pojma kako da nastavim. ,I nemam pojma kako da nastavim.
2.Neka su 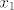 i i 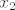 realna rjesenja jednadzbe realna rjesenja jednadzbe 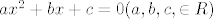 i vazi i vazi 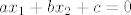 .Dokazi da je: a) .Dokazi da je: a)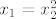 b) b) 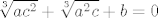 . .
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:30 sri, 17. 8. 2011 Naslov: Postano: 13:30 sri, 17. 8. 2011 Naslov: |
    |
|
|
1. U zadatku se traži da p bude cijeli broj tako da ti rješenje nikako ne može biti interval ili unija intervala realnih brojeva.
Diskriminanta te kvadratne jednadžbe je 1+4p. Rješenja će biti racionalna točno onda kada je 1+4p kvadrat nekog cijelog broja. Ako je [latex]1+4p=k^2[/latex], ispitaj kakav mora biti k da bi p bio cijeli broj.
[spoiler][latex]1+4p=k^2\Rightarrow p=\frac{k^2-1}{4}[/latex].
Ako je k paran broj onda je k oblika k=2m, gdje je m bilo koji cijeli broj pa je [latex]p=\frac{k^2-1}{4}=\frac{4m^2-1}{4}=\frac{2(2m^2)-1}{2\cdot 2}=\frac{1}{2}\cdot\frac{2(2m^2)-1}{2}[/latex]. Iz toga slijedi da p nikada nije cijeli broj jer je [latex]2(2m^2)-1[/latex] neparan pa nije dijeljiv s 2.
Ako je k neparan broj, onda je k oblika k=2m+1 pa je [latex]p=\frac{4m^2+4m+1-1}{4}=\frac{4m^2+4m}{4}=m^2+m=m(m+1)[/latex], gdje je m bilo koji cijeli broj. Dakle, broj p mora biti iz skupa [latex]\{m(m+1)~|~m\in\mathbb{Z}\}=\{0\cdot 1,1\cdot 2,2\cdot 3, 3\cdot 4,\dots\}[/latex][/spoiler]
2. Da bi jednadžba [latex]ax^2+bx+c[/latex] uopće imala dva realna rješenja, uvjeti na a, b i c moraju biti puno složeniji od a, b, c [latex]\in\mathbb{R}[/latex]. Mora biti [latex]a\neq 0[/latex] i [latex]b^2-4ac>0[/latex].
2a). Ako je [latex]x_2[/latex] realno rješenje, onda vrijedi [latex]ax_2^2+bx_2+c=0[/latex]. Ako oduzmemo od toga [latex]ax_1+bx_2+c=0[/latex], ostaje [latex]ax_2^2=ax_1[/latex]. Sa a smijemo podijeliti jer je [latex]a\neq 0[/latex].
2b). Iskoristi Vieteove formule i a) dio.
[spoiler][dtex]x_1x_2=\frac{c}{a}~\&~x_1=x_2^2\Rightarrow x_2^3=\frac{c}{a}\Rightarrow x_2=\left(\frac{c}{a}\right)^\frac{1}{3}\Rightarrow x_1=\left(\frac{c}{a}\right)^\frac{2}{3}[/dtex]
[dtex]x_1+x_2=-\frac{b}{a}\Rightarrow ax_1+ax_2=-b\Rightarrow a\left(\frac{c}{a}\right)^\frac{2}{3}+a\left(\frac{c}{a}\right)^\frac{1}{3}+b=0[/dtex]
[/spoiler]
1. U zadatku se traži da p bude cijeli broj tako da ti rješenje nikako ne može biti interval ili unija intervala realnih brojeva.
Diskriminanta te kvadratne jednadžbe je 1+4p. Rješenja će biti racionalna točno onda kada je 1+4p kvadrat nekog cijelog broja. Ako je 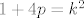 , ispitaj kakav mora biti k da bi p bio cijeli broj. , ispitaj kakav mora biti k da bi p bio cijeli broj.
| Spoiler [hidden; click to show]: | 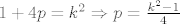 .
Ako je k paran broj onda je k oblika k=2m, gdje je m bilo koji cijeli broj pa je 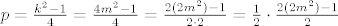 . Iz toga slijedi da p nikada nije cijeli broj jer je 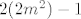 neparan pa nije dijeljiv s 2.
Ako je k neparan broj, onda je k oblika k=2m+1 pa je 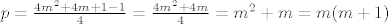 , gdje je m bilo koji cijeli broj. Dakle, broj p mora biti iz skupa 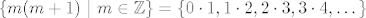 |
2. Da bi jednadžba 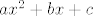 uopće imala dva realna rješenja, uvjeti na a, b i c moraju biti puno složeniji od a, b, c uopće imala dva realna rješenja, uvjeti na a, b i c moraju biti puno složeniji od a, b, c  . Mora biti . Mora biti 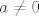 i i 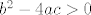 . .
2a). Ako je 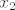 realno rješenje, onda vrijedi realno rješenje, onda vrijedi 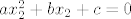 . Ako oduzmemo od toga . Ako oduzmemo od toga 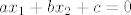 , ostaje , ostaje 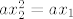 . Sa a smijemo podijeliti jer je . Sa a smijemo podijeliti jer je 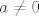 . .
2b). Iskoristi Vieteove formule i a) dio.
| Spoiler [hidden; click to show]: | [dtex]x_1x_2=\frac{c}{a}~\&~x_1=x_2^2\Rightarrow x_2^3=\frac{c}{a}\Rightarrow x_2=\left(\frac{c}{a}\right)^\frac{1}{3}\Rightarrow x_1=\left(\frac{c}{a}\right)^\frac{2}{3}[/dtex]
[dtex]x_1+x_2=-\frac{b}{a}\Rightarrow ax_1+ax_2=-b\Rightarrow a\left(\frac{c}{a}\right)^\frac{2}{3}+a\left(\frac{c}{a}\right)^\frac{1}{3}+b=0[/dtex]
|
_________________
The Dude Abides
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 12:44 pon, 22. 8. 2011 Naslov: Postano: 12:44 pon, 22. 8. 2011 Naslov: |
    |
|
|
Bojim se da indukcija nije dobra, jer se zbog promjene [i]n[/i]-a mijenjaju i svi elementi sume.
Podsjetnik: [tex]{4n \choose 4k+1} = {4n \choose 4n-4k-1}[/tex]
Dakle:[dtex]S := \sum_{k=0}^{n-1}{4n \choose 4k+1} = \sum_{k=0}^{n-1}{4n \choose 4n-4k-1} = \sum_{k=0}^{n-1}{4n \choose 4k+3}[/dtex]Nas zanima [tex]S[/tex].
Primijetimo:[dtex]2S = S+S = \sum_{k=0}^{n-1}{4n \choose 4k+1} + \sum_{k=0}^{n-1}{4n \choose 4k+3} = \sum_{k=0}^{2n-1}{4n \choose 2k+1} = \sum_{k=0}^{N-1}{2N \choose 2k+1}, \quad N := 2n.[/dtex]
Ostaje ti ovo za srediti. Ako zapnes, vrisni ovdje.
Bojim se da indukcija nije dobra, jer se zbog promjene n-a mijenjaju i svi elementi sume.
Podsjetnik: [tex]{4n \choose 4k+1} = {4n \choose 4n-4k-1}[/tex]
Dakle:[dtex]S := \sum_{k=0}^{n-1}{4n \choose 4k+1} = \sum_{k=0}^{n-1}{4n \choose 4n-4k-1} = \sum_{k=0}^{n-1}{4n \choose 4k+3}[/dtex]Nas zanima [tex]S[/tex].
Primijetimo:[dtex]2S = S+S = \sum_{k=0}^{n-1}{4n \choose 4k+1} + \sum_{k=0}^{n-1}{4n \choose 4k+3} = \sum_{k=0}^{2n-1}{4n \choose 2k+1} = \sum_{k=0}^{N-1}{2N \choose 2k+1}, \quad N := 2n.[/dtex]
Ostaje ti ovo za srediti. Ako zapnes, vrisni ovdje.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 2:30 sri, 24. 8. 2011 Naslov: Postano: 2:30 sri, 24. 8. 2011 Naslov: |
    |
|
|
Goran me pretekao, ali kad sam vec nakucao, evo...
Lako se pokaze da [tex]{4n \choose 4k+1}={4n \choose 4k+3}[/tex] opcenito [b]ne[/b] vrijedi. Stvar je u tome da uvrstis sto treba i onda pozbrajas unatrag:
[dtex]\begin{align*}
S &:= \sum_{k=0}^{n-1}{4n \choose 4k+1} = \sum_{k=0}^{n-1}{4n \choose 4n-4k-1} \\
&= {4n \choose 4n-1} + {4n \choose 4n-5} + \dots + {4n \choose 7} + {4n \choose 3} \\
&= {4n \choose 3} + {4n \choose 7} + \dots + {4n \choose 4n-5} + {4n \choose 4n-1} \\
&= \sum_{k=0}^{n-1}{4n \choose 4k+3}
\end{align*}[/dtex]
Sume zbrojis trivijalno, tako da uzimas elemente naizmjence, pa vise ne idu svaki cetvrti nego svaki drugi:
[dtex]S = \sum_{k=0}^{n-1}{4n \choose 4k+1} = {4n \choose 1} + {4n \choose 5} + \dots + {4n \choose 4n-7} + {4n \choose 4n-3}[/dtex]i[dtex]S = \sum_{k=0}^{n-1}{4n \choose 4k+3} = {4n \choose 3} + {4n \choose 7} + \dots + {4n \choose 4n-5} + {4n \choose 4n-1}[/dtex]Sad se to zbroji:[dtex]2S = S + S = {4n \choose 1} + {4n \choose 3} + {4n \choose 5} + {4n \choose 7} + \dots + {4n \choose 4n-7} + {4n \choose 4n-5} + {4n \choose 4n-3} + {4n \choose 4n-1} = \sum_{k=0}^{2n-1}{4n \choose 2k+1}[/dtex]
Ako ti treba ono sto nisam rijesio (naci koliko je zapravo [tex]2S[/tex]), pogledaj [url=http://www.proofwiki.org/wiki/Sum_of_Odd_Index_Binomial_Coefficients]ovdje[/url], no preporucam da ipak prvo sam probas.
Goran me pretekao, ali kad sam vec nakucao, evo...
Lako se pokaze da [tex]{4n \choose 4k+1}={4n \choose 4k+3}[/tex] opcenito ne vrijedi. Stvar je u tome da uvrstis sto treba i onda pozbrajas unatrag:
[dtex]\begin{align*}
S &:= \sum_{k=0}^{n-1}{4n \choose 4k+1} = \sum_{k=0}^{n-1}{4n \choose 4n-4k-1} \\
&= {4n \choose 4n-1} + {4n \choose 4n-5} + \dots + {4n \choose 7} + {4n \choose 3} \\
&= {4n \choose 3} + {4n \choose 7} + \dots + {4n \choose 4n-5} + {4n \choose 4n-1} \\
&= \sum_{k=0}^{n-1}{4n \choose 4k+3}
\end{align*}[/dtex]
Sume zbrojis trivijalno, tako da uzimas elemente naizmjence, pa vise ne idu svaki cetvrti nego svaki drugi:
[dtex]S = \sum_{k=0}^{n-1}{4n \choose 4k+1} = {4n \choose 1} + {4n \choose 5} + \dots + {4n \choose 4n-7} + {4n \choose 4n-3}[/dtex]i[dtex]S = \sum_{k=0}^{n-1}{4n \choose 4k+3} = {4n \choose 3} + {4n \choose 7} + \dots + {4n \choose 4n-5} + {4n \choose 4n-1}[/dtex]Sad se to zbroji:[dtex]2S = S + S = {4n \choose 1} + {4n \choose 3} + {4n \choose 5} + {4n \choose 7} + \dots + {4n \choose 4n-7} + {4n \choose 4n-5} + {4n \choose 4n-3} + {4n \choose 4n-1} = \sum_{k=0}^{2n-1}{4n \choose 2k+1}[/dtex]
Ako ti treba ono sto nisam rijesio (naci koliko je zapravo [tex]2S[/tex]), pogledaj ovdje, no preporucam da ipak prvo sam probas.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Tekster
Forumaš(ica)

Pridružen/a: 12. 07. 2011. (20:58:18)
Postovi: (1D)16
|
|
| [Vrh] |
|
|











