| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 11:54 ned, 1. 4. 2012 Naslov: |
    |
|
|
Kad napravis LU s parcijalnim pivotiranjem, dva puta rjesavas trokutasti sustav, s time da je parcijalno pivotiranje zapravo permutacija redaka, pa ti ispermutira elemente od [i]f[/i].
Kad napravis LU s parcijalnim pivotiranjem, dva puta rjesavas trokutasti sustav, s time da je parcijalno pivotiranje zapravo permutacija redaka, pa ti ispermutira elemente od f.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Dama Herc
Forumaš(ica)
Pridružen/a: 24. 09. 2010. (23:37:22)
Postovi: (12)16
Spol: 
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
|
| [Vrh] |
|
mono
Forumaš(ica)
Pridružen/a: 16. 09. 2011. (13:04:01)
Postovi: (E)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)
Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)
Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
| Postano: 15:15 sub, 7. 4. 2012 Naslov: |
|
|
|
Pa OK, Sylvesterov kriterij se obradi i na Linearnoj algebri, ja mislim. Nije to ''nešto specijalno što se radi samo na DIFRAFu''.
Prvo sam ti stavio link na englesku wikipediju, al sam se onda predomislio, jer tko zna kako barataš sa engleskim... Onda sam se sjetio da je to objašnjeno u skripti iz DIFRAFA i da će ti to možda biti lakše za iščitati.
http://en.wikipedia.org/wiki/Sylvester's_criterion
http://mat.gsia.cmu.edu/classes/QUANT/NOTES/chap1/node8.html
Znači, na ovom primjeru ti moraju determinante od matrica:
[latex]\begin{bmatrix}
4 \\
\end{bmatrix}[/latex],
[latex]\begin{bmatrix}
4 & 1 \\
1 & 2 \\
\end{bmatrix}[/latex],
[latex]\begin{bmatrix}
4 & 1 & 0 \\
1 & 2 & x \\
0 & x & 2 \\
\end{bmatrix}[/latex],
[latex]\begin{bmatrix}
4 & 1 & 0 & 0 \\
1 & 2 & x & 0 \\
0 & x & 2 & 1 \\
0 & 0 & 1 & 1 \\
\end{bmatrix}[/latex]
biti pozitivne.
Za prve dvije se to odmah vidi, a za druge dvije trebaš ručno provjeriti za kakve su x-eve determinante veće od 0.
Ima još načina za provjeriti da li je matrica pozitivno definitna, ali mislim da se ovaj najlakše primjeni na ovaj zadatak. Ako te zanima koji su to:
http://en.wikipedia.org/wiki/Positive-definite_matrix
Pa OK, Sylvesterov kriterij se obradi i na Linearnoj algebri, ja mislim. Nije to ''nešto specijalno što se radi samo na DIFRAFu''.
Prvo sam ti stavio link na englesku wikipediju, al sam se onda predomislio, jer tko zna kako barataš sa engleskim... Onda sam se sjetio da je to objašnjeno u skripti iz DIFRAFA i da će ti to možda biti lakše za iščitati.
http://en.wikipedia.org/wiki/Sylvester's_criterion
http://mat.gsia.cmu.edu/classes/QUANT/NOTES/chap1/node8.html
Znači, na ovom primjeru ti moraju determinante od matrica:
 ,
 ,
 ,
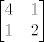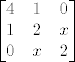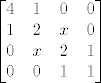
biti pozitivne.
Za prve dvije se to odmah vidi, a za druge dvije trebaš ručno provjeriti za kakve su x-eve determinante veće od 0.
Ima još načina za provjeriti da li je matrica pozitivno definitna, ali mislim da se ovaj najlakše primjeni na ovaj zadatak. Ako te zanima koji su to:
http://en.wikipedia.org/wiki/Positive-definite_matrix
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Dama Herc
Forumaš(ica)
Pridružen/a: 24. 09. 2010. (23:37:22)
Postovi: (12)16
Spol:
|
|
| [Vrh] |
|
googol
Forumaš(ica)
Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)
Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol:
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
| Postano: 1:30 pon, 9. 4. 2012 Naslov: |
|
|
|
[quote="Dama Herc"]Kako odrediti s0 i s2 kad nemam s', a imam s''?
Nadite parametre si kubicnog splajna s koji interpolira funkciju
f(x) = x*e^(x−1)
na ekvidistantnoj mrezi s n = 2 podintervala na intervalu [0, 1]. Rubni uvjeti za splajn su s′′ = f′′ u rubovima
intervala. Izracunajte vrijednosti tog splajna, njegove prve i druge derivacije u tocki x = 2/3 i pripadne prave pogreske.
hvala :D[/quote]
Da li vrijedi da imamo h=(1-0)/2, pa to znaci x0=0, x1=1/2, x2=1, (ili jos fali jedan x=1/2, ako imamo dva intervala [0, 1/2] i [1/2, 1]
Nekako me to sad buni.
[size=9][color=#999999]Added after 48 minutes:[/color][/size]
Ako je netko rjesavao 4. zadatak iz 2010., (predzadnja grupa), molila bih da provjerimo rjesenja bar za si:
ZAD: (10 bodova.) Nadite parametre si kubicnog splajna s koji interpolira funkciju
f(x) = (x + 1) cos x
na ekvidistantnoj mrezi s n = 2 podintervala na intervalu [0, PI/2]. Rubni uvjeti za splajn su s′′ = f′′ u rubovima
intervala. Izracunajte vrijednosti tog splajna, njegove prve i druge derivacije u tocki x = PI/3 i pripadne prave
pogreske.
Moja rjesenja:
s0=-0.17615
s1=0.96214
s2=-1.6859
s3=-1.960875
| Dama Herc (napisa): | Kako odrediti s0 i s2 kad nemam s', a imam s''?
Nadite parametre si kubicnog splajna s koji interpolira funkciju
f(x) = x*e^(x−1)
na ekvidistantnoj mrezi s n = 2 podintervala na intervalu [0, 1]. Rubni uvjeti za splajn su s′′ = f′′ u rubovima
intervala. Izracunajte vrijednosti tog splajna, njegove prve i druge derivacije u tocki x = 2/3 i pripadne prave pogreske.
hvala  |
Da li vrijedi da imamo h=(1-0)/2, pa to znaci x0=0, x1=1/2, x2=1, (ili jos fali jedan x=1/2, ako imamo dva intervala [0, 1/2] i [1/2, 1]
Nekako me to sad buni.
Added after 48 minutes:
Ako je netko rjesavao 4. zadatak iz 2010., (predzadnja grupa), molila bih da provjerimo rjesenja bar za si:
ZAD: (10 bodova.) Nadite parametre si kubicnog splajna s koji interpolira funkciju
f(x) = (x + 1) cos x
na ekvidistantnoj mrezi s n = 2 podintervala na intervalu [0, PI/2]. Rubni uvjeti za splajn su s′′ = f′′ u rubovima
intervala. Izracunajte vrijednosti tog splajna, njegove prve i druge derivacije u tocki x = PI/3 i pripadne prave
pogreske.
Moja rjesenja:
s0=-0.17615
s1=0.96214
s2=-1.6859
s3=-1.960875
|
|
| [Vrh] |
|
satja
Forumaš(ica)
Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
| Postano: 6:35 pon, 9. 4. 2012 Naslov: |
|
|
|
[quote="Anonymous"]jel bi mogo netko napisat kolko mu ispada M2f u 5.b zadatku proslogodisnjeg kolokvija, prva grupa? hvala[/quote]
Druga derivacija od [tex]f[/tex] je http://www.wolframalpha.com/input/?i=second+derivative+of+sqrt%283x%2B2%29 , kad promatramo apsolutnu vrijednost to je za nenegativne [tex]x[/tex] padajuća funkcija pa se njezini maksimumi na intervalima [0,2] i [2,c] postižu u točkama 0 i 2, redom. Vrijednosti dobiješ kad uvrstiš.
| Anonymous (napisa): | | jel bi mogo netko napisat kolko mu ispada M2f u 5.b zadatku proslogodisnjeg kolokvija, prva grupa? hvala |
Druga derivacija od [tex]f[/tex] je http://www.wolframalpha.com/input/?i=second+derivative+of+sqrt%283x%2B2%29 , kad promatramo apsolutnu vrijednost to je za nenegativne [tex]x[/tex] padajuća funkcija pa se njezini maksimumi na intervalima [0,2] i [2,c] postižu u točkama 0 i 2, redom. Vrijednosti dobiješ kad uvrstiš.
|
|
| [Vrh] |
|
Gost
|
| Postano: 8:35 pon, 9. 4. 2012 Naslov: |
|
|
|
[quote="satja"][quote="Anonymous"]jel bi mogo netko napisat kolko mu ispada M2f u 5.b zadatku proslogodisnjeg kolokvija, prva grupa? hvala[/quote]
Druga derivacija od [tex]f[/tex] je http://www.wolframalpha.com/input/?i=second+derivative+of+sqrt%283x%2B2%29 , kad promatramo apsolutnu vrijednost to je za nenegativne [tex]x[/tex] padajuća funkcija pa se njezini maksimumi na intervalima [0,2] i [2,c] postižu u točkama 0 i 2, redom. Vrijednosti dobiješ kad uvrstiš.[/quote]
hvala, zapravo me nije zanimalo za b, nego za a :/ krivo sam napisala, jer kad uvrstim da mi je taj maximum 0, zadatak mi nema smisla :?
| satja (napisa): | | Anonymous (napisa): | | jel bi mogo netko napisat kolko mu ispada M2f u 5.b zadatku proslogodisnjeg kolokvija, prva grupa? hvala |
Druga derivacija od [tex]f[/tex] je http://www.wolframalpha.com/input/?i=second+derivative+of+sqrt%283x%2B2%29 , kad promatramo apsolutnu vrijednost to je za nenegativne [tex]x[/tex] padajuća funkcija pa se njezini maksimumi na intervalima [0,2] i [2,c] postižu u točkama 0 i 2, redom. Vrijednosti dobiješ kad uvrstiš. |
hvala, zapravo me nije zanimalo za b, nego za a  krivo sam napisala, jer kad uvrstim da mi je taj maximum 0, zadatak mi nema smisla 
|
|
| [Vrh] |
|
satja
Forumaš(ica)
Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
| Postano: 8:56 pon, 9. 4. 2012 Naslov: |
|
|
|
[quote="Anonymous"]
hvala, zapravo me nije zanimalo za b, nego za a :/ krivo sam napisala, jer kad uvrstim da mi je taj maximum 0, zadatak mi nema smisla :?[/quote]
[tex]M_2(f)[/tex] na intervalu [tex][0,2][/tex] nije [tex]0[/tex], nego [tex]|f''(0)|[/tex].
| Anonymous (napisa): |
hvala, zapravo me nije zanimalo za b, nego za a krivo sam napisala, jer kad uvrstim da mi je taj maximum 0, zadatak mi nema smisla |
[tex]M_2(f)[/tex] na intervalu [tex][0,2][/tex] nije [tex]0[/tex], nego [tex]|f''(0)|[/tex].
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|
