| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
roolrr22
Forumaš(ica)

Pridružen/a: 09. 05. 2011. (20:50:51)
Postovi: (16)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 2:49 ned, 10. 6. 2012 Naslov: Postano: 2:49 ned, 10. 6. 2012 Naslov: |
    |
|
|
1. Oznaci bridove baze s [i]a[/i] i [i]b[/i], a visinu sa [i]c[/i]. Tada znas:
[tex]\begin{array}{l}
a : b = 1 : 2 \quad \Leftrightarrow \quad \displaystyle \frac{a}{b} = \frac{1}{2} \quad \Leftrightarrow \quad 2a = b, \\
c = 4, \\
\sqrt{a^2 + b^2 + c^2} = 4 \sqrt{6}.
\end{array}[/tex]
Dalje bi trebalo biti lako.
2. Slicno kao prvi, pa probaj sam postaviti. Primijeti samo da ti omjer daje tri medjusobno zavisne jednadzbe (svaki par bridova daje jednu), ali bilo koje dvije jesu nezavisne. Trecu opet dobijes od prostorne dijagonale.
[color=purple]@Svi ostali: Pustite covjeka da si ovo sam rijesi, da lako vidi je l' shvatio.[/color] :)
3. Ako se dobro sjecam, dijagonala pravilnog sesterokuta je dvostruko dulja od stranice. [b]AKO[/b] sam u pravu, onda imas da je povrsina tog presjeka [tex]P = dv = 2av[/tex], pri cemu je [i]d[/i] duljina te dijagonale, [i]a[/i] je duljina stranice, a [i]v[/i] je visina.
Znaci li ono "pravilna" i da su bocne strane okomite na bazu? Ako da, onda ti oplosje cini 6 pravokutnika sa stranicama [i]a[/i] i [i]v[/i], tj. [tex]O = 6av = 3(2av) = 3P[/tex].
Ovo mi je sumnjivo trivijalno, pa provjeri... ja nisam geometriju vidio od gimnazije. :oops:
U svakom slucaju, ideja je tu, a ti vidi vrijede li identiteti na koje se pozivam ([tex]d = 2a[/tex] i da su bocne strane pravokutnici).
Za cetvrti sam pozaboravljao pojmove ili, vjerojatnije, mene su drugacije ucili... ipak sam ja u gimnaziju isao u najranijim danima aktualne drzave. :djed:
1. Oznaci bridove baze s a i b, a visinu sa c. Tada znas:
[tex]\begin{array}{l}
a : b = 1 : 2 \quad \Leftrightarrow \quad \displaystyle \frac{a}{b} = \frac{1}{2} \quad \Leftrightarrow \quad 2a = b, \\
c = 4, \\
\sqrt{a^2 + b^2 + c^2} = 4 \sqrt{6}.
\end{array}[/tex]
Dalje bi trebalo biti lako.
2. Slicno kao prvi, pa probaj sam postaviti. Primijeti samo da ti omjer daje tri medjusobno zavisne jednadzbe (svaki par bridova daje jednu), ali bilo koje dvije jesu nezavisne. Trecu opet dobijes od prostorne dijagonale.
@Svi ostali: Pustite covjeka da si ovo sam rijesi, da lako vidi je l' shvatio. 
3. Ako se dobro sjecam, dijagonala pravilnog sesterokuta je dvostruko dulja od stranice. AKO sam u pravu, onda imas da je povrsina tog presjeka [tex]P = dv = 2av[/tex], pri cemu je d duljina te dijagonale, a je duljina stranice, a v je visina.
Znaci li ono "pravilna" i da su bocne strane okomite na bazu? Ako da, onda ti oplosje cini 6 pravokutnika sa stranicama a i v, tj. [tex]O = 6av = 3(2av) = 3P[/tex].
Ovo mi je sumnjivo trivijalno, pa provjeri... ja nisam geometriju vidio od gimnazije. 
U svakom slucaju, ideja je tu, a ti vidi vrijede li identiteti na koje se pozivam ([tex]d = 2a[/tex] i da su bocne strane pravokutnici).
Za cetvrti sam pozaboravljao pojmove ili, vjerojatnije, mene su drugacije ucili... ipak sam ja u gimnaziju isao u najranijim danima aktualne drzave. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
roolrr22
Forumaš(ica)

Pridružen/a: 09. 05. 2011. (20:50:51)
Postovi: (16)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 13:36 ned, 10. 6. 2012 Naslov: Postano: 13:36 ned, 10. 6. 2012 Naslov: |
    |
|
|
[quote="roolrr22"]Ispričavam se, četvrti zadatak sam krivo prepisao. Nema pravilne četverostrane prizme, samo piramide.[/quote]
Oke, čini mi se da sam ja gore isto malo krivo rekao ( :oops: ), ali ideja ti je promatrati trokut. Kut između brida i baze definira se kao kut između brida i njegove projekcije na bazu - gledaš još visinu i imaš (pravokutni) trokut.
Primijeti da su kutovi "lijepi", tj. to su kutovi koji se javljaju u jednakostraničnim, tj. jednakokračnim trokutima pa pokušaj onda sam zaključiti :)
| roolrr22 (napisa): | | Ispričavam se, četvrti zadatak sam krivo prepisao. Nema pravilne četverostrane prizme, samo piramide. |
Oke, čini mi se da sam ja gore isto malo krivo rekao (  ), ali ideja ti je promatrati trokut. Kut između brida i baze definira se kao kut između brida i njegove projekcije na bazu - gledaš još visinu i imaš (pravokutni) trokut. ), ali ideja ti je promatrati trokut. Kut između brida i baze definira se kao kut između brida i njegove projekcije na bazu - gledaš još visinu i imaš (pravokutni) trokut.
Primijeti da su kutovi "lijepi", tj. to su kutovi koji se javljaju u jednakostraničnim, tj. jednakokračnim trokutima pa pokušaj onda sam zaključiti 
|
|
| [Vrh] |
|
roolrr22
Forumaš(ica)

Pridružen/a: 09. 05. 2011. (20:50:51)
Postovi: (16)16
|
|
| [Vrh] |
|
roolrr22
Forumaš(ica)

Pridružen/a: 09. 05. 2011. (20:50:51)
Postovi: (16)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
roolrr22
Forumaš(ica)

Pridružen/a: 09. 05. 2011. (20:50:51)
Postovi: (16)16
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
|
| [Vrh] |
|
roolrr22
Forumaš(ica)

Pridružen/a: 09. 05. 2011. (20:50:51)
Postovi: (16)16
|
|
| [Vrh] |
|
Neno
Forumaš(ica)

Pridružen/a: 08. 02. 2008. (20:03:15)
Postovi: (98)16
Spol: 
Lokacija: Zagreb
|
 Postano: 14:38 pon, 11. 6. 2012 Naslov: Re: Četiri zadataka iz matematike - osnovna škola 8.r Postano: 14:38 pon, 11. 6. 2012 Naslov: Re: Četiri zadataka iz matematike - osnovna škola 8.r |
    |
|
|
[quote="roolrr22"]
4. Osnovni brid pravilne četverostrane piramide jest 10 cm. Kolike su duljine bočnog brida i visine piramide ako pobočka piramide s bazom zatvara kut od a) 45° b) 60° i c) 30°?[/quote]
vidim da bi trebalo dobiti:
[quote="roolrr22"] rješenja su a) b = 5√3 cm, h = 5 cm b) b = 5√5 cm, h = 5√3 cm c) b = 5√21 / 3 cm, h = 5√3 / 3 cm.
Hvala puno![/quote]
Prvo lagani uvod,
pravilna četverostrana piramida..... pravilna ... to znači da joj je baza pravilan mnogokut, ovdje: kvadrat, a spojnica vrha V, i središta S mnogokuta (ovdje kvadrata) je okomita na ravninu baze.
osnovni brid.. je brid na bazi
pobočni bridovi.. svi su jednake duljine
pobočka piramide.. to je strana piramide, to je trokut
a) [latex]45^\circ[/latex]
skiciraj bazu piramide, kvadrat ABCD sa središtem S. ucrtaj dijagonalu AC. duljina dijagonale svakog kvadrata je [latex]a\sqrt 2[/latex] pa je ovdje duljina dijagonale [latex]10\sqrt 2[/latex], pola dijagonale [latex]5\sqrt2[/latex]. Osnovni brid baze, kvadrata, je 10, znači da je udaljenost od S do stranice AD = 5 cm.
Na stranici AD stavi točku B' (nožište okomice iz S !). Ravnina, pobočka, koja prolazi točkama A,B',D, je nagnuta 45 st. prema vrhu piramide V, a iz vrha piramide ide okomica u središte baze. naravno da uočavaš pravokutni trokut, izvuci ga van na papir, skiciraj, suma kutova u svakom trokutu je 180 st. znači 180 st-45 st = kut AVS = 45 st. dobio si jednakokračan trokut, udaljenost od B' do S je jednaka udaljenosti od S do V, znam udaljenost od B' do S=5 cm, znači da je (njihov odgovor) [latex]\boxed{h=5\ cm}[/latex] :)
ajmo bočni brid b, Pitagorin teorem;
[latex]\\|VA|=b=\sqrt{|AS|^2+|SV|^2}=\sqrt{(5\sqrt2)^2+5^2}=\sqrt{5^2\cdot 2 + 5^2}=\sqrt{5^2(2+1)}=\boxed{5\sqrt3}\ cm[/latex]
b) [latex]60^\circ[/latex]
prvo pomoćna skica: trokut B'SV, kut u vrhu B' je 60 st, a kako je pravi kut u S, to kut SVB' može biti samo 30 st. Sad naštimaj da ispadne jednakostranični trokut, znači nadopuni skicu u vrhu V, tamo gdje je 30 st udvostruči ga sa još jednim od 30 st, nadodaj ga, i tako si formirao novi trokut, jednakostranični, sva tri kuta su 60 st, mogu uvrštavati u formulu za visinu jednakostraničnog trokuta, a meni će to zapravo biti visina piramide:
[latex]v_{jednakostranicnog\ trokuta}=h_{piramide}=\frac{a\sqrt3}{2}=\frac{2\cdot 5\sqrt3}{2}=\boxed{5\sqrt3\ cm}[/latex]
bočni brid b, opet Pitagora:
[latex]b=\sqrt{|AS|^2+h^2}=\sqrt{(5\sqrt2)^2+(5\sqrt3)^2}=\sqrt{5^2\cdot2+5^2\cdot3}=\sqrt{5^2(2+3)}=\boxed{5\sqrt5\ cm}[/latex]
c) [latex]30^\circ[/latex]
prvo pomoćna skica, trokut B'SV, kut VB'S 30 st, a budući je kut B'SV pravi kut, to kut B'VS može biti samo 60 st. Formiraj, naštimaj jednakostranični trokut tako da jasno vidiš u svakom vrhu 60 st, produlji prema dolje dužinu VS i novonastali vrh nazovi naprimjer V'.
Opet nastupa laganica, uvrštavanje u formulu jednakostraničnog trokuta
[latex]|B'S|=\frac{|VV'|\cdot\sqrt3}{2}\\|VV'|=2\cdot\frac{5}{\sqrt3}\cdot\frac{\sqrt3}{\sqrt3}=\frac{2\cdot5\cdot\sqrt3}{3}\\|VS|=\frac12|VV'|=h=\frac12\cdot \frac{2\cdot5\sqrt3}{3}=\boxed{\frac{5\sqrt3}{3}\ cm}[/latex]
bočni brid b, Pitagorin teorem:
[latex]b=|AV|=\sqrt{(5\sqrt2)^2+(\frac{5\sqrt3}{3})^2}=\sqrt{5^2\cdot2+\frac{5^2\cdot3}{3^2}}=\sqrt{5^2\cdot 2+\frac{5^2}{3}}=\sqrt{5^2(2+\frac13)}=5\sqrt{\frac73}=\frac{5\sqrt7}{\sqrt3}\cdot \frac{\sqrt3}{\sqrt3}=\boxed{\frac{5\sqrt{21}}{3}}\ cm.[/latex]
:lol:
| roolrr22 (napisa): |
4. Osnovni brid pravilne četverostrane piramide jest 10 cm. Kolike su duljine bočnog brida i visine piramide ako pobočka piramide s bazom zatvara kut od a) 45° b) 60° i c) 30°? |
vidim da bi trebalo dobiti:
| roolrr22 (napisa): | rješenja su a) b = 5√3 cm, h = 5 cm b) b = 5√5 cm, h = 5√3 cm c) b = 5√21 / 3 cm, h = 5√3 / 3 cm.
Hvala puno! |
Prvo lagani uvod,
pravilna četverostrana piramida..... pravilna ... to znači da joj je baza pravilan mnogokut, ovdje: kvadrat, a spojnica vrha V, i središta S mnogokuta (ovdje kvadrata) je okomita na ravninu baze.
osnovni brid.. je brid na bazi
pobočni bridovi.. svi su jednake duljine
pobočka piramide.. to je strana piramide, to je trokut
a) 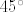
skiciraj bazu piramide, kvadrat ABCD sa središtem S. ucrtaj dijagonalu AC. duljina dijagonale svakog kvadrata je 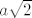 pa je ovdje duljina dijagonale pa je ovdje duljina dijagonale 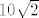 , pola dijagonale , pola dijagonale 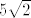 . Osnovni brid baze, kvadrata, je 10, znači da je udaljenost od S do stranice AD = 5 cm. . Osnovni brid baze, kvadrata, je 10, znači da je udaljenost od S do stranice AD = 5 cm.
Na stranici AD stavi točku B' (nožište okomice iz S !). Ravnina, pobočka, koja prolazi točkama A,B',D, je nagnuta 45 st. prema vrhu piramide V, a iz vrha piramide ide okomica u središte baze. naravno da uočavaš pravokutni trokut, izvuci ga van na papir, skiciraj, suma kutova u svakom trokutu je 180 st. znači 180 st-45 st = kut AVS = 45 st. dobio si jednakokračan trokut, udaljenost od B' do S je jednaka udaljenosti od S do V, znam udaljenost od B' do S=5 cm, znači da je (njihov odgovor) 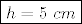 
ajmo bočni brid b, Pitagorin teorem;
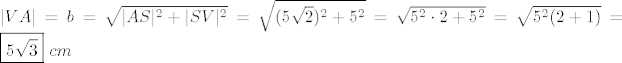
b) 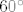
prvo pomoćna skica: trokut B'SV, kut u vrhu B' je 60 st, a kako je pravi kut u S, to kut SVB' može biti samo 30 st. Sad naštimaj da ispadne jednakostranični trokut, znači nadopuni skicu u vrhu V, tamo gdje je 30 st udvostruči ga sa još jednim od 30 st, nadodaj ga, i tako si formirao novi trokut, jednakostranični, sva tri kuta su 60 st, mogu uvrštavati u formulu za visinu jednakostraničnog trokuta, a meni će to zapravo biti visina piramide:
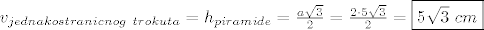
bočni brid b, opet Pitagora:
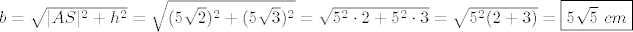
c) 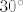
prvo pomoćna skica, trokut B'SV, kut VB'S 30 st, a budući je kut B'SV pravi kut, to kut B'VS može biti samo 60 st. Formiraj, naštimaj jednakostranični trokut tako da jasno vidiš u svakom vrhu 60 st, produlji prema dolje dužinu VS i novonastali vrh nazovi naprimjer V'.
Opet nastupa laganica, uvrštavanje u formulu jednakostraničnog trokuta
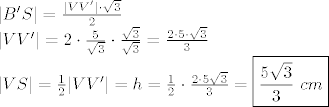
bočni brid b, Pitagorin teorem:
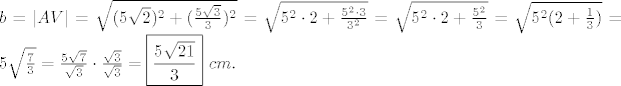

|
|
| [Vrh] |
|
roolrr22
Forumaš(ica)

Pridružen/a: 09. 05. 2011. (20:50:51)
Postovi: (16)16
|
|
| [Vrh] |
|
|








