| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
weirdie
Forumaš(ica)

Pridružen/a: 18. 11. 2005. (15:39:31)
Postovi: (69)16
Spol: 
Lokacija: na svom aršinu prostora
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
weirdie
Forumaš(ica)

Pridružen/a: 18. 11. 2005. (15:39:31)
Postovi: (69)16
Spol: 
Lokacija: na svom aršinu prostora
|
|
| [Vrh] |
|
irena0102
Forumaš(ica)


Pridružen/a: 01. 02. 2010. (11:49:52)
Postovi: (45)16
Spol: 
|
|
| [Vrh] |
|
CrniVG
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (22:44:19)
Postovi: (23)16
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 7:33 uto, 17. 4. 2012 Naslov: Postano: 7:33 uto, 17. 4. 2012 Naslov: |
    |
|
|
Pretpostavimo da imamo [latex]x, y[/latex] takve da je [latex]xQy[/latex] i [latex]yQx[/latex]. Uočimo definiciju od [latex]Q[/latex]: kada bi bilo [latex]x = y[/latex] ili [latex]y = x[/latex], trivijalno bi slijedilo [latex]x = y[/latex] čime bi bila dokazana antisimetričnost. Preostaje nam još slučaj kad je [latex]xRy[/latex] i [latex]yRx[/latex]. Sada antisimetričnost slijedi iz antisimetričnosti od [latex]R[/latex].
Potpuno je ista ideja i za tranzitivnost.
EDIT: sorry, sad vidim da pitas za slucaj kada je u definiciji [latex]x\neq y[/latex] meni je to učitalo kao 1. grupu :D:D
Ali kontradikciju i trebaš dobiti, samo valja obratiti pozornost na kontradkciju s čim: da se dokaže antisimetričnost, prvo treba pretpostaviti da postoje [latex]x, y[/latex] takvi da je [latex]xQy[/latex] i [latex]yQx[/latex]. U ovom slučaju će ta pretpostavka dovesti do kontradikcije, tj. dobije se [latex]x=y[/latex] i [latex]x\neq y[/latex], ali to ne znači da ne vrijedi antisimetričnost, već pretpostavka nije dobra, tj. uopće ne može doći do slučaja kada je [latex]xQy[/latex] i [latex]yQx[/latex], pa je antisimetričnost trivijalno zadovoljena. (Sjećam se profesora Pažanina kako je često to znao ilustrirati: "Nema gdje propasti!")
Pretpostavimo da imamo 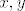 takve da je takve da je 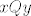 i i 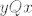 . Uočimo definiciju od . Uočimo definiciju od 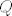 : kada bi bilo : kada bi bilo 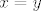 ili ili 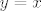 , trivijalno bi slijedilo , trivijalno bi slijedilo 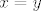 čime bi bila dokazana antisimetričnost. Preostaje nam još slučaj kad je čime bi bila dokazana antisimetričnost. Preostaje nam još slučaj kad je 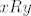 i i 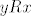 . Sada antisimetričnost slijedi iz antisimetričnosti od . Sada antisimetričnost slijedi iz antisimetričnosti od 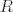 . .
Potpuno je ista ideja i za tranzitivnost.
EDIT: sorry, sad vidim da pitas za slucaj kada je u definiciji 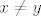 meni je to učitalo kao 1. grupu meni je to učitalo kao 1. grupu  
Ali kontradikciju i trebaš dobiti, samo valja obratiti pozornost na kontradkciju s čim: da se dokaže antisimetričnost, prvo treba pretpostaviti da postoje 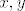 takvi da je takvi da je 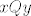 i i 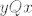 . U ovom slučaju će ta pretpostavka dovesti do kontradikcije, tj. dobije se . U ovom slučaju će ta pretpostavka dovesti do kontradikcije, tj. dobije se 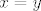 i i 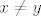 , ali to ne znači da ne vrijedi antisimetričnost, već pretpostavka nije dobra, tj. uopće ne može doći do slučaja kada je , ali to ne znači da ne vrijedi antisimetričnost, već pretpostavka nije dobra, tj. uopće ne može doći do slučaja kada je 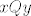 i i 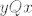 , pa je antisimetričnost trivijalno zadovoljena. (Sjećam se profesora Pažanina kako je često to znao ilustrirati: "Nema gdje propasti!") , pa je antisimetričnost trivijalno zadovoljena. (Sjećam se profesora Pažanina kako je često to znao ilustrirati: "Nema gdje propasti!")
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
 Postano: 12:25 uto, 17. 4. 2012 Naslov: Postano: 12:25 uto, 17. 4. 2012 Naslov: |
    |
|
|
Sory, radilo se o prvoj grupi, meni su se u glavi zamijenile jer sam prvo išla rješavati onu drugu grupu. Malo me buni ta logika, da li se to može shvatiti ovako: kako nam ne vrijedi x=y, onda ne vrijedi ni xQy i yQx (jer nam pretpostavka ne valja zbog dobivene kontradikcije, kako Flame reče), pa zbog obrata po kontrapoziciji trivijalno važi antisimetričnost? ili sam nešto krivo shvatila?
Sory, radilo se o prvoj grupi, meni su se u glavi zamijenile jer sam prvo išla rješavati onu drugu grupu. Malo me buni ta logika, da li se to može shvatiti ovako: kako nam ne vrijedi x=y, onda ne vrijedi ni xQy i yQx (jer nam pretpostavka ne valja zbog dobivene kontradikcije, kako Flame reče), pa zbog obrata po kontrapoziciji trivijalno važi antisimetričnost? ili sam nešto krivo shvatila?
_________________
Granice mogućega možemo odrediti samo onda ako ih prijeđemo odlaskom u nemoguće
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 12:54 uto, 17. 4. 2012 Naslov: Postano: 12:54 uto, 17. 4. 2012 Naslov: |
    |
|
|
Vrlo je jednostavo, u logici prvog reda se tvrdnja zapisuje ovako:
[latex]\forall x\forall y ((xQy \wedge yQx)\rightarrow (x=y))[/latex]
Mi smo ustvrdili da je [latex]xQy \wedge yQx [/latex] antitautologija, tj. ne vrijedi nikad. Ali [latex]0 \rightarrow P[/latex] je tautologija, bez obzira na [latex]P[/latex] pa je gornja formula valjanja.
Ako gledamo obrat po kontrapoziciji, imamo:
[latex]\exists x\exists y ((xQy \wedge yQx)\wedge (x\neq y))[/latex]
i sad slicno kao maloprije imamo da je [latex]0\wedge P[/latex] antitautologija bez obzira na [latex]P[/latex], pa formula nije istitinita niti za jedan [latex]x,y[/latex].
EDIT: ovdje se poprilicno slobodno razbacujem pojmovima poput tautologije i antitautologije, ali ciljao sam na razumljivost :)
Takodjer, jednostavno mozemo reci ovako, kad god je ispunjeno [latex]xQy \wedge yQx [/latex] nuzno mora biti [latex]x=y[/latex]. Ali ako premisa nikad nije ispunjena, nemamo problema :D
Vrlo je jednostavo, u logici prvog reda se tvrdnja zapisuje ovako:
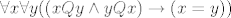
Mi smo ustvrdili da je 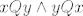 antitautologija, tj. ne vrijedi nikad. Ali antitautologija, tj. ne vrijedi nikad. Ali 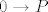 je tautologija, bez obzira na je tautologija, bez obzira na  pa je gornja formula valjanja. pa je gornja formula valjanja.
Ako gledamo obrat po kontrapoziciji, imamo:
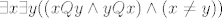
i sad slicno kao maloprije imamo da je 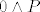 antitautologija bez obzira na antitautologija bez obzira na  , pa formula nije istitinita niti za jedan , pa formula nije istitinita niti za jedan 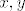 . .
EDIT: ovdje se poprilicno slobodno razbacujem pojmovima poput tautologije i antitautologije, ali ciljao sam na razumljivost 
Takodjer, jednostavno mozemo reci ovako, kad god je ispunjeno 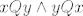 nuzno mora biti nuzno mora biti 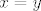 . Ali ako premisa nikad nije ispunjena, nemamo problema . Ali ako premisa nikad nije ispunjena, nemamo problema 
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 19:48 uto, 17. 4. 2012 Naslov: Postano: 19:48 uto, 17. 4. 2012 Naslov: |
    |
|
|
Jasno je da takvih funkcija ima manje ili jednako od [latex]2^{c}[/latex]. Postavlja se pitanje kako [latex]2^c[/latex] uloziti u trazeni skup. Ideja je naci funkciju koja na konacnom intervalu zadovoljava trazeno svojstvo (ovdje surjektivnost), a zatim naizmjenice "lijepiti" kopije te funkcije, odnosno proizvoljne funkcije na tom intervalu. Tako postizemo periodicnost.
Ovdje konkretno trebamo naci surjekciju s konacnog intervala na [latex]\mathbb{R}[/latex]. Meni recimo pada napamet [latex]\operatorname{tg}:\langle -\frac{\pi}{2}, \frac{\pi}{2} \rangle \rightarrow \mathbb{R}[/latex], ali moze posluziti bilo koja dok god je domena konacan interval. Sada definiramo preslikavanje
[latex]\phi : \mathbb{R}^{\langle -\frac{\pi}{2}, \frac{\pi}{2} \rangle} \rightarrow S[/latex]
[latex](\phi f)(x) := \left \{ \begin{array}{cl}
\operatorname{tg} x & ,\quad x\in \langle -\frac{\pi}{2}+2k\pi, \frac{\pi}{2}+2k\pi \rangle , \; k\in \mathbb{Z} \\
f(x-(2k+1)\pi) & ,\quad x\in \langle -\frac{\pi}{2}+(2k+1)\pi, \frac{\pi}{2}+(2k+1)\pi \rangle , \; k\in \mathbb{Z} \\
0 & ,\quad inace
\end{array}[/latex]
Tako definirano preslikavanje je injekcija (kao prosirenje funkcije [latex]f[/latex]), njena slika su surjektivne funkcije (zbog tangensa) te periodicne s periodom [latex]2\pi[/latex] zbog nacina kako smo definirali preslikavnje. Sada slijedi da je [latex]2^c = k(\mathbb{R}^{\langle -\frac{\pi}{2}, \frac{\pi}{2} \rangle}) \leq k(S)[/latex].
Bonus pitanje: sto ako bismo zahtijevali da su surjektivna periodicka preslikavanja na [latex]\mathbb{R}[/latex] jos i neprekidna?
Jasno je da takvih funkcija ima manje ili jednako od 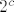 . Postavlja se pitanje kako . Postavlja se pitanje kako 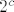 uloziti u trazeni skup. Ideja je naci funkciju koja na konacnom intervalu zadovoljava trazeno svojstvo (ovdje surjektivnost), a zatim naizmjenice "lijepiti" kopije te funkcije, odnosno proizvoljne funkcije na tom intervalu. Tako postizemo periodicnost. uloziti u trazeni skup. Ideja je naci funkciju koja na konacnom intervalu zadovoljava trazeno svojstvo (ovdje surjektivnost), a zatim naizmjenice "lijepiti" kopije te funkcije, odnosno proizvoljne funkcije na tom intervalu. Tako postizemo periodicnost.
Ovdje konkretno trebamo naci surjekciju s konacnog intervala na  . Meni recimo pada napamet . Meni recimo pada napamet 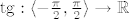 , ali moze posluziti bilo koja dok god je domena konacan interval. Sada definiramo preslikavanje , ali moze posluziti bilo koja dok god je domena konacan interval. Sada definiramo preslikavanje
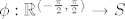
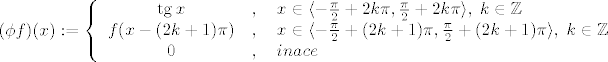
Tako definirano preslikavanje je injekcija (kao prosirenje funkcije  ), njena slika su surjektivne funkcije (zbog tangensa) te periodicne s periodom ), njena slika su surjektivne funkcije (zbog tangensa) te periodicne s periodom 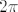 zbog nacina kako smo definirali preslikavnje. Sada slijedi da je zbog nacina kako smo definirali preslikavnje. Sada slijedi da je 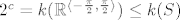 . .
Bonus pitanje: sto ako bismo zahtijevali da su surjektivna periodicka preslikavanja na  jos i neprekidna? jos i neprekidna?
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
 Postano: 22:48 uto, 17. 4. 2012 Naslov: Postano: 22:48 uto, 17. 4. 2012 Naslov: |
    |
|
|
@Flame:
1) Može pomoć sa tvojim pitanjem u vezi neprekidnih?
2) Na vježbama smo imali ovakav zadatak: Koliko ima periodičkih funkcija s [latex]\mathbb{R}[/latex] u [latex]\mathbb{R}[/latex] koje svaku vrijednost iz intervala [latex]\langle 0, 1 \rangle[/latex] poprimaju beskonačno mnogo puta?
Definirali smo funkciju ovako:
[latex](\phi f)(x) := \left \{ \begin{array}{cl}
\operatorname{sin} \frac{1}{x} & ,\quad x\in \langle 2k, 2k+1 ] , \; k\in \mathbb{Z} \\
f(x) & ,\quad x\in \langle 2k+1, 2k+2 ] , \; k\in \mathbb{Z} \\
\end{array}[/latex]
[latex]f: \langle 1, 2] \to [10,11][/latex]
Sada me buni sljedeće: nismo li od funkcije f trebali "prekopirati" vrijednosti s domene od f, onako kako si ti to napravio? Jer, ovako f može na svakom tom intervalu drugačije izgledati pa neće biti periodično.
Skužih... f je definirana za x-eve iz <1,2] pa moramo prilagoditi x svakako :)
@Flame:
1) Može pomoć sa tvojim pitanjem u vezi neprekidnih?
2) Na vježbama smo imali ovakav zadatak: Koliko ima periodičkih funkcija s  u u  koje svaku vrijednost iz intervala koje svaku vrijednost iz intervala 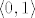 poprimaju beskonačno mnogo puta? poprimaju beskonačno mnogo puta?
Definirali smo funkciju ovako:
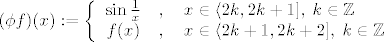

Sada me buni sljedeće: nismo li od funkcije f trebali "prekopirati" vrijednosti s domene od f, onako kako si ti to napravio? Jer, ovako f može na svakom tom intervalu drugačije izgledati pa neće biti periodično.
Skužih... f je definirana za x-eve iz <1,2] pa moramo prilagoditi x svakako 
_________________
Granice mogućega možemo odrediti samo onda ako ih prijeđemo odlaskom u nemoguće
Zadnja promjena: komaPMF; 23:22 uto, 17. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 23:29 uto, 17. 4. 2012 Naslov: Postano: 23:29 uto, 17. 4. 2012 Naslov: |
    |
|
|
[quote="komaPMF"]@Flame:
1) Može pomoć sa tvojim pitanjem u vezi neprekidnih?
2) Na vježbama smo imali ovakav zadatak: Koliko ima periodičkih funkcija s [latex]\mathbb{R}[/latex] u [latex]\mathbb{R}[/latex] koje svaku vrijednost iz intervala [latex]\langle 0, 1 \rangle[/latex] poprimaju beskonačno mnogo puta?
Definirali smo funkciju ovako:
[latex](\phi f)(x) := \left \{ \begin{array}{cl}
\operatorname{sin} \frac{1}{x} & ,\quad x\in \langle 2k, 2k+1 ] , \; k\in \mathbb{Z} \\
f(x) & ,\quad x\in \langle 2k+1, 2k+2 ] , \; k\in \mathbb{Z} \\
\end{array}[/latex]
[latex]f: \langle 1, 2] \to [10,11][/latex]
Sada me buni sljedeće: nismo li od funkcije f trebali "prekopirati" vrijednosti s domene od f, onako kako si ti to napravio? Jer, ovako f može na svakom tom intervalu drugačije izgledati pa neće biti periodično.[/quote]
1) Evo asistent je pristigao u pomoc! :D
Razlog je jednostavan, ako je [latex]f[/latex] periodicka, onda ima neki period [latex]t[/latex] pa sve vrijednosti postize na segmentu [latex][0,t][/latex]. Ali posto je [latex]f[/latex] neprekidna, [latex]f([0,t])[/latex] je kompaktan, odnosno segment, dakle nemogu se postici sve vrijednosti iz [latex]\mathbb{R}[/latex]
2) Pretpostavljam da je rijec o lapsusu, jer funkcija [latex]f[/latex] u tim tockama uopce nije definirana. Mislim, lako ju je dodefinirati, ali to treba napraviti tako da je onda periodicna s periodom duljine intervala, sto sam ja u neku ruku i napravio.
| komaPMF (napisa): | @Flame:
1) Može pomoć sa tvojim pitanjem u vezi neprekidnih?
2) Na vježbama smo imali ovakav zadatak: Koliko ima periodičkih funkcija s  u u  koje svaku vrijednost iz intervala koje svaku vrijednost iz intervala 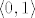 poprimaju beskonačno mnogo puta? poprimaju beskonačno mnogo puta?
Definirali smo funkciju ovako:
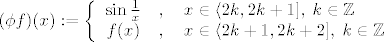

Sada me buni sljedeće: nismo li od funkcije f trebali "prekopirati" vrijednosti s domene od f, onako kako si ti to napravio? Jer, ovako f može na svakom tom intervalu drugačije izgledati pa neće biti periodično. |
1) Evo asistent je pristigao u pomoc! 
Razlog je jednostavan, ako je  periodicka, onda ima neki period periodicka, onda ima neki period  pa sve vrijednosti postize na segmentu pa sve vrijednosti postize na segmentu 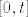 . Ali posto je . Ali posto je  neprekidna, neprekidna, 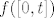 je kompaktan, odnosno segment, dakle nemogu se postici sve vrijednosti iz je kompaktan, odnosno segment, dakle nemogu se postici sve vrijednosti iz 
2) Pretpostavljam da je rijec o lapsusu, jer funkcija  u tim tockama uopce nije definirana. Mislim, lako ju je dodefinirati, ali to treba napraviti tako da je onda periodicna s periodom duljine intervala, sto sam ja u neku ruku i napravio. u tim tockama uopce nije definirana. Mislim, lako ju je dodefinirati, ali to treba napraviti tako da je onda periodicna s periodom duljine intervala, sto sam ja u neku ruku i napravio.
|
|
| [Vrh] |
|
irena0102
Forumaš(ica)


Pridružen/a: 01. 02. 2010. (11:49:52)
Postovi: (45)16
Spol: 
|
|
| [Vrh] |
|
weirdie
Forumaš(ica)

Pridružen/a: 18. 11. 2005. (15:39:31)
Postovi: (69)16
Spol: 
Lokacija: na svom aršinu prostora
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
 Postano: 17:27 ned, 3. 6. 2012 Naslov: Postano: 17:27 ned, 3. 6. 2012 Naslov: |
    |
|
|
Kolokvij 2011., druga grupa, zadatak 4.: https://docs.google.com/viewer?a=v&pid=sites&srcid=ZGVmYXVsdGRvbWFpbnxtYXRobmFzdGF2YXxneDoxNzRlZjhhOWY3YmFmYzU2
Može li se to riješiti ovako:
Imamo niz nula i jedinica, napravimo bijekciju td ga preslikamo u broj 0,a0a1a2a3.... , a ako u nizu imamo sve jedinice, preslikamo ga u broj 1. Tako dobijemo u binarnom zapisu svaki broj iz [0,1]. i sad su skupovi slični ? Čini mi se da je ovo netočno, ali ništa bolje nisam mogla smisliti... Molim nekog da ukaže na greške :D
Kolokvij 2011., druga grupa, zadatak 4.: https://docs.google.com/viewer?a=v&pid=sites&srcid=ZGVmYXVsdGRvbWFpbnxtYXRobmFzdGF2YXxneDoxNzRlZjhhOWY3YmFmYzU2
Može li se to riješiti ovako:
Imamo niz nula i jedinica, napravimo bijekciju td ga preslikamo u broj 0,a0a1a2a3.... , a ako u nizu imamo sve jedinice, preslikamo ga u broj 1. Tako dobijemo u binarnom zapisu svaki broj iz [0,1]. i sad su skupovi slični ? Čini mi se da je ovo netočno, ali ništa bolje nisam mogla smisliti... Molim nekog da ukaže na greške 
_________________
Granice mogućega možemo odrediti samo onda ako ih prijeđemo odlaskom u nemoguće
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:19 ned, 3. 6. 2012 Naslov: Postano: 18:19 ned, 3. 6. 2012 Naslov: |
    |
|
|
[quote="komaPMF"]Kolokvij 2011., druga grupa, zadatak 4.: https://docs.google.com/viewer?a=v&pid=sites&srcid=ZGVmYXVsdGRvbWFpbnxtYXRobmFzdGF2YXxneDoxNzRlZjhhOWY3YmFmYzU2
Može li se to riješiti ovako:
Imamo niz nula i jedinica, napravimo bijekciju td ga preslikamo u broj 0,a0a1a2a3.... , a ako u nizu imamo sve jedinice, preslikamo ga u broj 1. Tako dobijemo u binarnom zapisu svaki broj iz [0,1]. i sad su skupovi slični ? Čini mi se da je ovo netočno, ali ništa bolje nisam mogla smisliti... Molim nekog da ukaže na greške :D[/quote]
Greška je u tome što to preslikavanje nije injekcija (pa onda ni sličnost), npr. [latex](0.0111\ldots)_2 = (0.1)_2 = \frac{1}{2}[/latex].
No, onda primijetiš da su [latex](0, 1, 1, 1, \ldots)[/latex] i [latex](1, 0, 0, 0, \ldots)[/latex] dva različita niza između kojih ne postoji neki treći niz, pa taj skup nizova s leksikografskim uređajem nije gust. Naprotiv, [latex]([0, 1], <)[/latex] je gust, dakle, to nisu slični skupovi.
Greška je u tome što to preslikavanje nije injekcija (pa onda ni sličnost), npr. 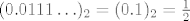 . .
No, onda primijetiš da su 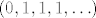 i i 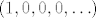 dva različita niza između kojih ne postoji neki treći niz, pa taj skup nizova s leksikografskim uređajem nije gust. Naprotiv, dva različita niza između kojih ne postoji neki treći niz, pa taj skup nizova s leksikografskim uređajem nije gust. Naprotiv, 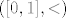 je gust, dakle, to nisu slični skupovi. je gust, dakle, to nisu slični skupovi.
|
|
| [Vrh] |
|
|























