| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 8:14 sub, 19. 10. 2013 Naslov: (ne)popularni zadaci iz kolokvija/bliceva/zadaca (DIFRAF) Postano: 8:14 sub, 19. 10. 2013 Naslov: (ne)popularni zadaci iz kolokvija/bliceva/zadaca (DIFRAF) |
    |
|
|
u zadnje vrijeme me mailom dosta kolega pita iste zadatke, pa mi se čini najzgodnije staviti rješenja na forum - koristit će budućim generacijama ako nikom drugom. :wink:
znači, jedan od takvih zadataka je 12.d) iz prve zadaće koji je skoro isti kao 2.b) iz prvog blica s vježbi 2009. linkovi:
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/zadaca1.pdf
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/blic1.pdf
(formalno rješenje zadatka iz zadaće)
[tex]
S=\{(2q,\frac{1}{m}):q \in \mathbb{Q}, \; m\in \mathbb{Z}\setminus \{0\} \} [/tex]
Budući da je [tex]f:\mathbb{Q} \to \mathbb{Q}, \quad f(q)=2q[/tex] bijekcija,
dani skup jednak je [tex]S=\{(q,\frac{1}{m}):q \in \mathbb{Q}, m\in \mathbb{Z}\setminus \{0\} \}[/tex]
Kad skiciramo skup, čini se da bi skup gomilišta mogao biti
[tex] A=\{(x,\frac{1}{m}) : x \in \mathbb{R}, \, m\in \mathbb{Z}\setminus \{0\} \}\cup \{(x,0) : x\in \mathbb{R}\} [/tex]
Pokažimo sada da za proizvoljni [tex](x,y)\in A[/tex] i proizvoljni [tex]\varepsilon >0[/tex] postoji [tex](x_0,y_0) \in S\setminus \{(x,y)\}[/tex] t.d. [tex]d((x,y),(x_0,y_0))< \varepsilon[/tex].
Odnosno da proizvoljna [tex]K((x,y), \varepsilon)[/tex] sadrži [tex](x_0,y_0) \in S\setminus \{(x,y)\}[/tex].
Neka je [tex](x,y)\in A[/tex], [tex]\varepsilon >0[/tex]
[b]1°)[/b] [tex]y=\frac{1}{m}, \, m\in \mathbb{Z}\setminus \{0\}[/tex]
[b]a)[/b] [tex]x\in \mathbb{Q}[/tex]
[tex](\exists n \in \mathbb{N}) \; \frac{1}{n}<\varepsilon \\
(x_0,y_0)=(x+\frac{1}{n},\frac{1}{m}) \in S \Rightarrow
d((x,y),(x_0,y_0))=\sqrt{\frac{1}{n}^2+0}=\frac{1}{n}<\varepsilon[/tex]
[b]b)[/b] [tex]x\in \mathbb{R} \setminus \mathbb{Q}[/tex]
Zbog gustoće [tex]\mathbb{Q}[/tex] u [tex]\mathbb{R}:[/tex]
[tex]
(\exists q \in \mathbb{Q}) \; |x-q|< \varepsilon \\
(x_0,y_0)=(q,\frac{1}{m}) \in S \Rightarrow
d((x,y),(x_0,y_0))=\sqrt{(x-q)^2+0}=|x-q|<\varepsilon[/tex]
[b]2°)[/b] [tex]y=0[/tex]
[b]a)[/b] [tex]x\in \mathbb{Q}[/tex]
[tex](\exists m \in \mathbb{N}) \; \frac{1}{m}< \varepsilon \\
(x_0,y_0)=(x,\frac{1}{m})\in S \Rightarrow
d((x,y),(x_0, y_0))=\frac{1}{m}<\varepsilon[/tex]
[b]b)[/b] [tex]x\in \mathbb{R} \setminus \mathbb{Q}[/tex]
[tex](\exists m \in \mathbb{N}) \; \frac{1}{m}< \frac{\varepsilon }{\sqrt{2}} \\
(\exists q \in \mathbb{Q}) \; |x-q|< \frac{\varepsilon}{\sqrt{2}} [/tex]
[tex](x_0,y_0)=(q,\frac{1}{m}) \Rightarrow d((x,y),(x_0,y_0))=\sqrt{(x-q)^2+(\frac{1}{m})^2}<\varepsilon[/tex]
I to su svi mogući slučajevi! Znači dokazali smo da je [tex]A\subseteq S'[/tex].
Također, uočimo da su u [tex]A[/tex] sva gomilišta jer ako je [tex]y\neq \frac{1}{m}, y\neq 0[/tex] nemamo nikakvu garanciju da ćemo moći pronaći odgovarajući [tex]y_0[/tex] tako da razlika [tex]|y-y_0|[/tex] bude dovoljno mala.
[size=9][color=#999999]Added after 23 minutes:[/color][/size]
Drugo često postavljeno pitanje:
Da li je za zatvorene [tex]A_i\subseteq \mathbb{R}, \: i=1,...,n[/tex] i [tex]A=A_1\times ... \times A_n \subseteq \mathbb{R}^n[/tex] zatvoren?
Odgovor je DA, a evo i dokaza:
Pokazat ćemo da je [tex]A[/tex] zatvoren na način da pokažemo da sadrži sva svoja gomilišta.
Neka je [tex]a=(a_1,...,a_n)\in A'[/tex]. To znači da je i [tex]a\in \overline{A}[/tex], pa prema teoremu sa predavanja znamo da postoji niz u [tex]A[/tex] kojem je [tex]a[/tex] limes.
Nazovimo taj niz [tex]a^k=(a_1^k,...,a_n^k)[/tex].
Sada iz [tex]a^k\to a[/tex] slijedi [tex]a_i^k\to a_i, \; i=1,...,n[/tex]
No znamo da je [tex]a_i^k \in A_i, \; k\in \mathbb{N}[/tex]. Budući da je [tex]A_i \subseteq \mathbb{R}[/tex] zatvoren, svaki niz u [tex]A_i[/tex] koji konvergira u [tex]\mathbb{R}[/tex] ima limes u [tex]A_i[/tex].
Svaki koordinatni podniz je primjer takvog niza pa vrijedi [tex]a_i \in A_i, \; i=1,...,n[/tex], odnosno [tex]a\in A[/tex].
Vidimo da [tex]a\in A' \Rightarrow a\in A[/tex], pa je [tex]A[/tex] zatvoren.
u zadnje vrijeme me mailom dosta kolega pita iste zadatke, pa mi se čini najzgodnije staviti rješenja na forum - koristit će budućim generacijama ako nikom drugom. 
znači, jedan od takvih zadataka je 12.d) iz prve zadaće koji je skoro isti kao 2.b) iz prvog blica s vježbi 2009. linkovi:
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/zadaca1.pdf
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/blic1.pdf
(formalno rješenje zadatka iz zadaće)
[tex]
S=\{(2q,\frac{1}{m}):q \in \mathbb{Q}, \; m\in \mathbb{Z}\setminus \{0\} \} [/tex]
Budući da je [tex]f:\mathbb{Q} \to \mathbb{Q}, \quad f(q)=2q[/tex] bijekcija,
dani skup jednak je [tex]S=\{(q,\frac{1}{m}):q \in \mathbb{Q}, m\in \mathbb{Z}\setminus \{0\} \}[/tex]
Kad skiciramo skup, čini se da bi skup gomilišta mogao biti
[tex] A=\{(x,\frac{1}{m}) : x \in \mathbb{R}, \, m\in \mathbb{Z}\setminus \{0\} \}\cup \{(x,0) : x\in \mathbb{R}\} [/tex]
Pokažimo sada da za proizvoljni [tex](x,y)\in A[/tex] i proizvoljni [tex]\varepsilon >0[/tex] postoji [tex](x_0,y_0) \in S\setminus \{(x,y)\}[/tex] t.d. [tex]d((x,y),(x_0,y_0))< \varepsilon[/tex].
Odnosno da proizvoljna [tex]K((x,y), \varepsilon)[/tex] sadrži [tex](x_0,y_0) \in S\setminus \{(x,y)\}[/tex].
Neka je [tex](x,y)\in A[/tex], [tex]\varepsilon >0[/tex]
1°) [tex]y=\frac{1}{m}, \, m\in \mathbb{Z}\setminus \{0\}[/tex]
a) [tex]x\in \mathbb{Q}[/tex]
[tex](\exists n \in \mathbb{N}) \; \frac{1}{n}<\varepsilon \\
(x_0,y_0)=(x+\frac{1}{n},\frac{1}{m}) \in S \Rightarrow
d((x,y),(x_0,y_0))=\sqrt{\frac{1}{n}^2+0}=\frac{1}{n}<\varepsilon[/tex]
b) [tex]x\in \mathbb{R} \setminus \mathbb{Q}[/tex]
Zbog gustoće [tex]\mathbb{Q}[/tex] u [tex]\mathbb{R}:[/tex]
[tex]
(\exists q \in \mathbb{Q}) \; |x-q|< \varepsilon \\
(x_0,y_0)=(q,\frac{1}{m}) \in S \Rightarrow
d((x,y),(x_0,y_0))=\sqrt{(x-q)^2+0}=|x-q|<\varepsilon[/tex]
2°) [tex]y=0[/tex]
a) [tex]x\in \mathbb{Q}[/tex]
[tex](\exists m \in \mathbb{N}) \; \frac{1}{m}< \varepsilon \\
(x_0,y_0)=(x,\frac{1}{m})\in S \Rightarrow
d((x,y),(x_0, y_0))=\frac{1}{m}<\varepsilon[/tex]
b) [tex]x\in \mathbb{R} \setminus \mathbb{Q}[/tex]
[tex](\exists m \in \mathbb{N}) \; \frac{1}{m}< \frac{\varepsilon }{\sqrt{2}} \\
(\exists q \in \mathbb{Q}) \; |x-q|< \frac{\varepsilon}{\sqrt{2}} [/tex]
[tex](x_0,y_0)=(q,\frac{1}{m}) \Rightarrow d((x,y),(x_0,y_0))=\sqrt{(x-q)^2+(\frac{1}{m})^2}<\varepsilon[/tex]
I to su svi mogući slučajevi! Znači dokazali smo da je [tex]A\subseteq S'[/tex].
Također, uočimo da su u [tex]A[/tex] sva gomilišta jer ako je [tex]y\neq \frac{1}{m}, y\neq 0[/tex] nemamo nikakvu garanciju da ćemo moći pronaći odgovarajući [tex]y_0[/tex] tako da razlika [tex]|y-y_0|[/tex] bude dovoljno mala.
Added after 23 minutes:
Drugo često postavljeno pitanje:
Da li je za zatvorene [tex]A_i\subseteq \mathbb{R}, \: i=1,...,n[/tex] i [tex]A=A_1\times ... \times A_n \subseteq \mathbb{R}^n[/tex] zatvoren?
Odgovor je DA, a evo i dokaza:
Pokazat ćemo da je [tex]A[/tex] zatvoren na način da pokažemo da sadrži sva svoja gomilišta.
Neka je [tex]a=(a_1,...,a_n)\in A'[/tex]. To znači da je i [tex]a\in \overline{A}[/tex], pa prema teoremu sa predavanja znamo da postoji niz u [tex]A[/tex] kojem je [tex]a[/tex] limes.
Nazovimo taj niz [tex]a^k=(a_1^k,...,a_n^k)[/tex].
Sada iz [tex]a^k\to a[/tex] slijedi [tex]a_i^k\to a_i, \; i=1,...,n[/tex]
No znamo da je [tex]a_i^k \in A_i, \; k\in \mathbb{N}[/tex]. Budući da je [tex]A_i \subseteq \mathbb{R}[/tex] zatvoren, svaki niz u [tex]A_i[/tex] koji konvergira u [tex]\mathbb{R}[/tex] ima limes u [tex]A_i[/tex].
Svaki koordinatni podniz je primjer takvog niza pa vrijedi [tex]a_i \in A_i, \; i=1,...,n[/tex], odnosno [tex]a\in A[/tex].
Vidimo da [tex]a\in A' \Rightarrow a\in A[/tex], pa je [tex]A[/tex] zatvoren.
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 12:44 pet, 20. 12. 2013 Naslov: Postano: 12:44 pet, 20. 12. 2013 Naslov: |
    |
|
|
dug s jučerašnjih demonstratura:
9. zadatak iz http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/zadaca_df.pdf (ovaj sa *)
(rješenje bez upotrebe sfernih koordinata)
računanjem limesa iz definicije [latex]\frac{\partial f}{\partial x}(0,0,0), \; \frac{\partial f}{\partial y}(0,0,0), \; \frac{\partial f}{\partial z}(0,0,0)[/latex] lako se dobije da vrijedi [latex]\frac{\partial f}{\partial x}(0,0,0)=\frac{\partial f}{\partial y}(0,0,0)= \frac{\partial f}{\partial z}(0,0,0)=0[/latex].
Dakle ako postoji [latex]Df(0,0,0)[/latex], tada je njegov matrični prikaz u paru kanonskih baza jednak [latex](0 \quad 0 \quad 0)[/latex], odnosno [latex]Df(0,0,0)[/latex] je nul-operator.
Provjerimo vrijedi li [latex]Df(0,0,0)=0[/latex].
Računamo:
[latex]\displaystyle \lim_{(x,y,z) \to (0,0,0)} \frac{\| f(x,y,z)-f(0,0,0)-0((x,y,z)-(0,0,0))\|}{\|(x,y,z,)\|}=\displaystyle \lim_{(x,y,z) \to (0,0,0)} \frac{|\frac{x^2y^2z^2}{x^4+y^4+z^4} |}{\sqrt{x^2+y^2+z^2}}[/latex]
Sad prema AG nejednakosti imamo:
[latex]\sqrt[3]{x^2y^2z^2} \leq \frac{x^2+y^2+z^2}{3}[/latex]
[latex]x^2y^2z^2 \leq \frac{(x^2+y^2+z^2)^3}{27}[/latex]
Pa imamo:
[latex]\frac{|\frac{x^2y^2z^2}{x^4+y^4+z^4} |}{\sqrt{x^2+y^2+z^2}} \leq \frac{1}{27} \frac{(x^2+y^2+z^2)^2\sqrt{x^2+y^2+z^2}}{x^4+y^4+z^4}[/latex]
Prema AK nejednakosti imamo:
[latex]\frac{x^2+y^2+z^2}{3} \leq \sqrt{\frac{x^4+y^4+z^4}{3}}[/latex]
[latex]\frac{(x^2+y^2+z^2)^2}{9} \leq \frac{x^4+y^4+z^4}{3}[/latex]
Sad je:
[latex]0 \leq \frac{|\frac{x^2y^2z^2}{x^4+y^4+z^4} |}{\sqrt{x^2+y^2+z^2}} \leq \frac{1}{27} \frac{(x^2+y^2+z^2)^2\sqrt{x^2+y^2+z^2}}{x^4+y^4+z^4} \leq \frac{1}{9} \frac{(x^4+y^4+z^4)\sqrt{x^2+y^2+z^2}}{x^4+y^4+z^4}=\frac{1}{9}\sqrt{x^2+y^2+z^2[/latex]
Kad [latex](x,y,z) \to (0,0,0)[/latex], skroz desni izraz teži u [latex]0[/latex], pa je prema teoremu o sendviču
[latex]\displaystyle \lim_{(x,y,z) \to (0,0,0)} \frac{\| f(x,y,z)-f(0,0,0)-0((x,y,z)-(0,0,0))\|}{\|(x,y,z,)\|}=0[/latex]
Dakle, prema definiciji diferencijabilnosti, [latex]f[/latex] je diferencijabilna u [latex](0,0,0)[/latex] i [latex]Df(0,0,0)=0[/latex].
dug s jučerašnjih demonstratura:
9. zadatak iz http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/zadaca_df.pdf (ovaj sa *)
(rješenje bez upotrebe sfernih koordinata)
računanjem limesa iz definicije  lako se dobije da vrijedi lako se dobije da vrijedi 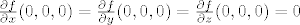 . .
Dakle ako postoji 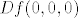 , tada je njegov matrični prikaz u paru kanonskih baza jednak , tada je njegov matrični prikaz u paru kanonskih baza jednak 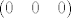 , odnosno , odnosno 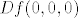 je nul-operator. je nul-operator.
Provjerimo vrijedi li 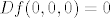 . .
Računamo:
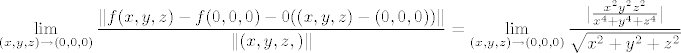
Sad prema AG nejednakosti imamo:
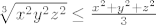
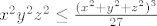
Pa imamo:

Prema AK nejednakosti imamo:
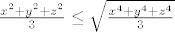
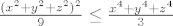
Sad je:

Kad 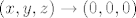 , skroz desni izraz teži u , skroz desni izraz teži u  , pa je prema teoremu o sendviču , pa je prema teoremu o sendviču
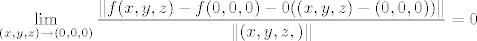
Dakle, prema definiciji diferencijabilnosti,  je diferencijabilna u je diferencijabilna u  i i 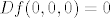 . .
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 13:52 pet, 20. 12. 2013 Naslov: Postano: 13:52 pet, 20. 12. 2013 Naslov: |
    |
|
|
I još me nekoliko ljudi pitalo 5. zadatak iz http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/zadaca3.pdf, pa evo rješenja i ovdje:
Znači imamo bilinearnu funkciju [latex]f: \mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^p[/latex].
Po definiciji bilinearnosti to znači:
[latex]f(\alpha x_1 + \beta x_2, y)=\alpha f(x_1,y)+\beta f(x_2,y)[/latex]
[latex]f(x,\gamma y_1 + \delta y_2)=\gamma f(x,y_1)+\delta f(x,y_2)[/latex]
Cilj nam je za proizvoljni [latex]c \in \mathbb{R}^n \times \mathbb{R}^m[/latex] dobiti:
[latex]f(c+h)-f(c)=L(c)h+r(h)[/latex], gdje je [latex]L(c)[/latex] linearni operator koji ovisi o [latex]c[/latex],
a [latex]r[/latex] funkcija t.d. [latex]\displaystyle \lim_{h \to 0} \frac{\|r(h)\|}{\|h\|}=0[/latex]
Onda ćemo dobiti:
[latex]\displaystyle \lim_{h \to 0} \frac{\|f(c+h)-f(c)-L(c)h\|}{\|h\|}=\displaystyle \lim_{h \to 0} \frac{\|r(h)\|}{\|h\|}=0[/latex]
Odnosno, vrijedit će [latex]Df(c)=L(c)[/latex].
Uzmimo [latex]c=(x,y) \in \mathbb{R}^n \times \mathbb{R}^m, \; h=(h_1, h_2) \in \mathbb{R}^n \times \mathbb{R}^m[/latex]
[latex]f(x+h_1, y+h_2)-f(x,y)=(bilinearnost)=f(x,y)+f(x,h_2)+f(h_1,y)+f(h_1,h_2)-f(x,y)=f(x,h_2)+f(h_1,y)+f(h_1,h_2)[/latex]
Provjerimo jesmo li dobili što nam treba:
[latex]L(x,y)(h_1,h_2)=f(x,h_2)+f(h_1,y)[/latex] je zbog linearnosti od [latex]f[/latex] u obje varijable linearni operator (provjerite!).
Treba jos samo vidjeti da je
[latex]\displaystyle \lim_{(h_1,h_2) \to (0,0)} \frac{\|f(h_1,h_2)\|}{\|(h_1,h_2)\|}=0[/latex]
Neka je:
[latex]h_1= \displaystyle \sum_{i=1}^{n}h_i^{(1)}e_i[/latex]
[latex]h_2= \displaystyle \sum_{j=1}^{m}h_j^{(2)}e_j[/latex]
Pa imamo:
[latex]\frac{\|f(h_1,h_2)\|}{\|(h_1,h_2)\|}=\frac{\|f(\displaystyle \sum_{i=1}^{n}h_i^{(1)}e_i, \displaystyle \sum_{j=1}^{m}h_j^{(2)}e_j )\|}{\|(h_1,h_2)\|}=(bilinearnost)=\frac{\|\displaystyle \sum_{i=1}^{n}\displaystyle \sum_{j=1}^{m}h_i^{(1)}h_j^{(2)}f(e_i, e_j)\|}{\|(h_1,h_2)\|}[/latex]
Sada na brojnik dva puta primjenimo nejednakost trokuta (za obje sume) i raspišemo
[latex]\|(h_1,h_2)\|=\sqrt{\displaystyle \sum_{k=1}^{n}(h_k^{(1)})^2+ \displaystyle \sum_{l=1}^{m}(h_l^{(2)})^2}[/latex]
[latex]0 \leq \frac{\|f(h_1,h_2)\|}{\|(h_1,h_2)\|} \leq \frac{\displaystyle \sum_{i=1}^{n}\displaystyle \sum_{j=1}^{m}\|h_i^{(1)}h_j^{(2)}f(e_i, e_j)\|}{\|(h_1,h_2)\|}}=\frac{\displaystyle \sum_{i=1}^{n}\displaystyle \sum_{j=1}^{m}|h_i^{(1)}| |h_j^{(2)}| \|f(e_i, e_j)\|}{\sqrt{\displaystyle \sum_{k=1}^{n}(h_k^{(1)})^2+ \displaystyle \sum_{l=1}^{m}(h_l^{(2)})^2}} \\ \leq \frac{\displaystyle \sum_{i=1}^{n}\displaystyle \sum_{j=1}^{m}|h_i^{(1)}| |h_j^{(2)}| \|f(e_i, e_j)\|}{\sqrt{\displaystyle \sum_{k=1}^{n}(h_k^{(1)})^2}} \leq \displaystyle \sum_{i=1}^{n}\displaystyle \sum_{j=1}^{m}\frac{|h_i^{(1)}| |h_j^{(2)}| \|f(e_i, e_j)\|}{\sqrt{(h_i^{(1)})^2}}=\displaystyle \sum_{i=1}^{n}\displaystyle \sum_{j=1}^{m}|h_j^{(2)}| \|f(e_i, e_j)\|}[/latex]
I sad kad [latex](h_1,h_2) \to 0[/latex], onda [latex]h_2 \to 0[/latex], a koordinate od [latex]h_2[/latex] su upravo [latex]h_j^{(2)}[/latex], pa vrijedi [latex]h_j^{(2)} \to 0, \; j=1,...,m[/latex].
Odnosno dobivena gornja ograda teži u [latex]0[/latex].
Dakle prema teoremu o sendviču, stvarno vrijedi:
[latex]\displaystyle \lim_{(h_1,h_2) \to (0,0)} \frac{\|f(h_1,h_2)\|}{\|(h_1,h_2)\|}=0[/latex]
Pa je [latex]Df(x,y)(h_1,h_2)=L(x,y)(h_1,h_2)=f(x,h_2)+f(h_1,y)[/latex].
(znam da su zbunjujući svi ovi indeksi, recite ako treba nešto dodatno pojasniti)
I još me nekoliko ljudi pitalo 5. zadatak iz http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/zadaca3.pdf, pa evo rješenja i ovdje:
Znači imamo bilinearnu funkciju 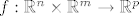 . .
Po definiciji bilinearnosti to znači:
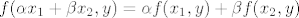
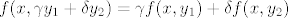
Cilj nam je za proizvoljni 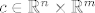 dobiti: dobiti:
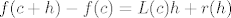 , gdje je , gdje je 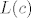 linearni operator koji ovisi o linearni operator koji ovisi o  , ,
a  funkcija t.d. funkcija t.d. 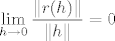
Onda ćemo dobiti:
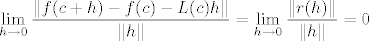
Odnosno, vrijedit će 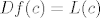 . .
Uzmimo 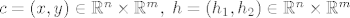
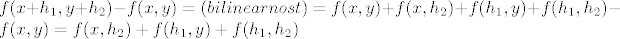
Provjerimo jesmo li dobili što nam treba:
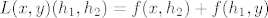 je zbog linearnosti od je zbog linearnosti od  u obje varijable linearni operator (provjerite!). u obje varijable linearni operator (provjerite!).
Treba jos samo vidjeti da je
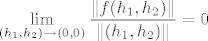
Neka je:
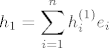
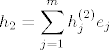
Pa imamo:
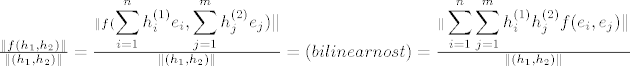
Sada na brojnik dva puta primjenimo nejednakost trokuta (za obje sume) i raspišemo
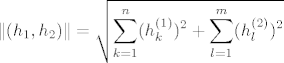
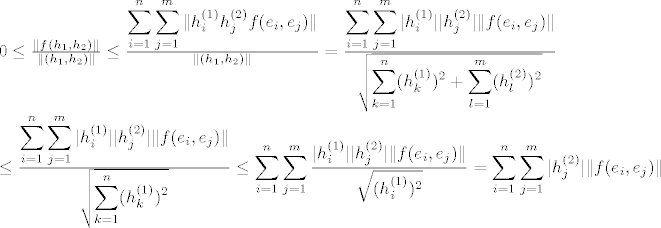
I sad kad  , onda , onda  , a koordinate od , a koordinate od 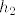 su upravo su upravo 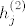 , pa vrijedi , pa vrijedi  . .
Odnosno dobivena gornja ograda teži u  . .
Dakle prema teoremu o sendviču, stvarno vrijedi:
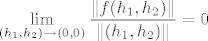
Pa je  . .
(znam da su zbunjujući svi ovi indeksi, recite ako treba nešto dodatno pojasniti)
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 11:29 čet, 26. 12. 2013 Naslov: Postano: 11:29 čet, 26. 12. 2013 Naslov: |
    |
|
|
još jedan zadatak:
1.10 iz http://web.math.pmf.unizg.hr/nastava/difraf/dif/vjezbe7.pdf
Da bi skalarni produkt [latex]\langle a, x \rangle[/latex] bio dobro definiran, mora vrijediti [latex]x \in \mathbb{R}^n[/latex].
Također, budući da je [latex]b \in \mathbb{R}^3[/latex], zbroj [latex]\langle a, x \rangle \cdot y + \cos \|x\|^2 \cdot b[/latex] će biti dobro definiran za [latex]y\in \mathbb{R}^3[/latex].
Dakle, domena je [latex]\mathbb{R}^n \times \mathbb{R}^3[/latex] i vrijedi [latex]f:\mathbb{R}^n \times \mathbb{R}^3 \to \mathbb{R}^3[/latex].
Jedan način za određivanje [latex]Df(x_0,y_0)[/latex] je promatranje funkcije kao [latex]f:\mathbb{R}^{n+3} \to \mathbb{R}^3[/latex] i određivanje parcijalnih derivacija na [latex]\mathbb{R}^{n+3}[/latex].
Ja ću pokazati drugi, čini mi se malo spretniji, način.
Neka je [latex]h=(h_1, h_2) \in \mathbb{R}^n \times \mathbb{R}^3 [/latex].
Tada vrijedi:
[latex]Df(x_0,y_0)(h_1, h_2)=\left[ {\begin{array}{cc}
\frac{\partial f}{\partial x}(x_0,y_0) & \frac{\partial f}{\partial y}(x_0,y_0)
\end{array} } \right] \cdot \left[ {\begin{array}{cc}
h_1 \\ h_2
\end{array} } \right]=\frac{\partial f}{\partial x}(x_0,y_0)h_1 + \frac{\partial f}{\partial y}(x_0,y_0)h_2[/latex]
Pri čemu vrijedi [latex]\frac{\partial f}{\partial x}(x_0,y_0) \in L(\mathbb{R}^n, \mathbb{R}^3), \; \frac{\partial f}{\partial y}(x_0,y_0) \in L(\mathbb{R}^3, \mathbb{R}^3)[/latex].
Odredimo prvo [latex]\frac{\partial f}{\partial x}(x_0,y_0)[/latex].
Za [latex](x_0,y_0) \in \mathbb{R}^n \times \mathbb{R}^3 [/latex] definiramo:
[latex]f_1(x)=\langle a, x \rangle \cdot y_0, \; f_2(x)=\cos \|x\|^2 \cdot b[/latex]
Sada je prema pravilu za diferencijal zbroja:
[latex]\frac{\partial f}{\partial x}(x_0,y_0)=Df_1(x_0)+Df_2(x_0)[/latex]
Iz Leibnizovog pravila dobijemo:
[latex]g(x)=\langle a, x \rangle, \; Dg(x_0)h=\langle a, h \rangle [/latex]
Iz pravila deriviranja kompozicije:
[latex]l(x)=\cos \|x\|^2, \; Dl(x_0)h=-2\sin \|x_0\|^2\langle x_0, h \rangle [/latex]
Sad primijenimo pravilo za deriviranje umnoška na [latex]f_1[/latex] i [latex]f_2 \;[/latex] ([latex]y_0, \; b[/latex] su konstante) i dobijemo:
[latex]\frac{\partial f}{\partial x}(x_0,y_0)h=\langle a, h \rangle \cdot y_0-2\sin \|x_0\|^2\langle x_0, h \rangle \cdot b[/latex]
Sad odredimo [latex]\frac{\partial f}{\partial y}(x_0,y_0)[/latex].
Za [latex](x_0,y_0) \in \mathbb{R}^n \times \mathbb{R}^3 [/latex] definiramo:
[latex]g(y)=\langle a, x_0 \rangle \cdot y[/latex]
Sad je [latex]\frac{\partial f}{\partial y}(x_0,y_0)=Dg(y_0)[/latex].
Prema pravilu za deriviranje umnoška (sad je [latex]\langle a, x_0 \rangle[/latex] konstanta, pa je [latex]g[/latex] umnožak konstante i identitete) dobijemo:
[latex]\frac{\partial f}{\partial y}(x_0,y_0)h=Dg(y_0)h=\langle a, x_0 \rangle \cdot h[/latex]
Znači vrijedi:
[latex]Df(x_0,y_0)(h_1, h_2)=\frac{\partial f}{\partial x}(x_0,y_0)h_1 + \frac{\partial f}{\partial y}(x_0,y_0)h_2= \\ \langle a, h_1 \rangle \cdot y_0-2\sin \|x_0\|^2\langle x_0, h_1 \rangle \cdot b+\langle a, x_0 \rangle \cdot h_2[/latex]
još jedan zadatak:
1.10 iz http://web.math.pmf.unizg.hr/nastava/difraf/dif/vjezbe7.pdf
Da bi skalarni produkt  bio dobro definiran, mora vrijediti bio dobro definiran, mora vrijediti  . .
Također, budući da je  , zbroj , zbroj 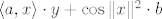 će biti dobro definiran za će biti dobro definiran za 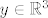 . .
Dakle, domena je 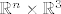 i vrijedi i vrijedi  . .
Jedan način za određivanje 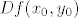 je promatranje funkcije kao je promatranje funkcije kao 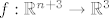 i određivanje parcijalnih derivacija na i određivanje parcijalnih derivacija na 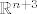 . .
Ja ću pokazati drugi, čini mi se malo spretniji, način.
Neka je 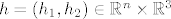 . .
Tada vrijedi:
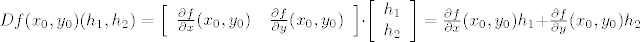
Pri čemu vrijedi 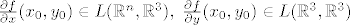 . .
Odredimo prvo 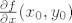 . .
Za 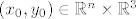 definiramo: definiramo:
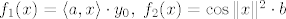
Sada je prema pravilu za diferencijal zbroja:
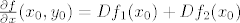
Iz Leibnizovog pravila dobijemo:
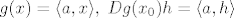
Iz pravila deriviranja kompozicije:
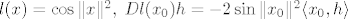
Sad primijenimo pravilo za deriviranje umnoška na 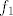 i i 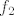 ( ( su konstante) i dobijemo: su konstante) i dobijemo:
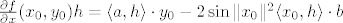
Sad odredimo 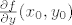 . .
Za 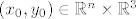 definiramo: definiramo:
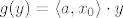
Sad je 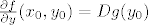 . .
Prema pravilu za deriviranje umnoška (sad je 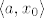 konstanta, pa je konstanta, pa je  umnožak konstante i identitete) dobijemo: umnožak konstante i identitete) dobijemo:
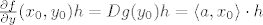
Znači vrijedi:
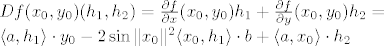
|
|
| [Vrh] |
|
|









