| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 16:30 pon, 15. 11. 2004 Naslov: zadatak, dva..? Postano: 16:30 pon, 15. 11. 2004 Naslov: zadatak, dva..? |
    |
|
|
1. Nadite bar jednu trojku (A,B,C) prirodnih brojeva manjih od 10 t.d. je
broj (A,B,C)b potpuni kvadrat za svaku bazu b ? b>max{A,B,C}
2. Zadana je baza b i tri medusobno razlicite znamenke sustava s bazom b kojima je suma jednaka b-1 i od kojih niti jedna nije 0. Promatramo sumu svih brojeva kojima se zapis u bazi b sastoji od tri zadane znamenke. Odredte sve baze b za koje je ta suma veca od 1000 i manja od 2000?
1. Nadite bar jednu trojku (A,B,C) prirodnih brojeva manjih od 10 t.d. je
broj (A,B,C)b potpuni kvadrat za svaku bazu b ? b>max{A,B,C}
2. Zadana je baza b i tri medusobno razlicite znamenke sustava s bazom b kojima je suma jednaka b-1 i od kojih niti jedna nije 0. Promatramo sumu svih brojeva kojima se zapis u bazi b sastoji od tri zadane znamenke. Odredte sve baze b za koje je ta suma veca od 1000 i manja od 2000?
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 17:44 pon, 15. 11. 2004 Naslov: Re: zadatak, dva..? Postano: 17:44 pon, 15. 11. 2004 Naslov: Re: zadatak, dva..? |
    |
|
|
[quote="Anonymous"]1. Nadite bar jednu trojku (A,B,C) prirodnih brojeva manjih od 10 t.d. je
broj (A,B,C)b potpuni kvadrat za svaku bazu b ? b>max{A,B,C}
[/quote]
[latex](1,0,0)[/latex] :wink:
[quote]
2. Zadana je baza b i tri medusobno razlicite znamenke sustava s bazom b kojima je suma jednaka b-1 i od kojih niti jedna nije 0. Promatramo sumu svih brojeva kojima se zapis u bazi b sastoji od tri zadane znamenke. Odredte sve baze b za koje je ta suma veca od 1000 i manja od 2000?[/quote]
Pretpostavimo da imamo bazu [latex]B[/latex] i sve takve triplete [latex]a_i,b_i,c_i[/latex]. Vidljivo je da je [latex]B\geq 7[/latex], jer je namanji triplet koji zadovoljava trazeno svojstvo [latex](3,2,1)[/latex].
BSOMP da vrijedi [latex]a_i>b_i>c_i[/latex] Poredajmo te brojeve kao sumu
[latex]\left.\matrix{
&a_1&b_1&c_1\cr
&a_1&c_1&b_1\cr
&&\vdots&\cr
+&c_n&b_n&a_n&\cr
&}\right.[/latex]
U svakom stupcu se za svaki [latex]i[/latex] svaki od [latex]a_i,b_i,c_i[/latex] pojavljuje tocno dvaput, pa je suma svakog stupca jednaka (jer je [latex]a_i+b_i+c_i=B-1[/latex])
[latex]\displaystyle \sum\limits_{i=1}^n 2(a_i+b_i+c_i)=2nB-2n[/latex]
Suma je onda jednaka (suma svega skupa)
[latex]\displaystyle (2nB-2n)B^2+(2nB-2n)B+(2nB-2n)=2nB^3-2n=\Sigma(B,n)[/latex]
No, ono sto zelimo, jest da je ta suma
[latex]B^3\leq \Sigma(B,n)\leq 2B^3[/latex]
Ako je [latex]n[/latex] veci od [latex]1[/latex], onda iz
[latex]2(n-1)B^3\leq 2n[/latex] slijedi [latex] B^3\leq {n\over n-1}[/latex], pa je [latex]B\leq \root 3 \of 2[/latex], jer je [latex]{n\over n-1}\leq 2[/latex], no to je nemoguce. Dakle, [latex]n=1[/latex].
Eh, ali uvjet [latex]n=1[/latex] zadovoljavaju samo [latex]B\leq 8[/latex]. Za [latex]B=9[/latex] je [latex]n>1[/latex], jer postoje tripleti [latex](4,3,1),(5,2,1)[/latex], a za [latex]B=8[/latex] samo [latex](4,2,1)[/latex]. Sasvim je jasno da [latex]B_1=7[/latex] i [latex]B_2=8[/latex] zadovoljavaju trazenu nejednakost, pa je to rjesenje.
'ave fun!
Sinisa
| Anonymous (napisa): | 1. Nadite bar jednu trojku (A,B,C) prirodnih brojeva manjih od 10 t.d. je
broj (A,B,C)b potpuni kvadrat za svaku bazu b ? b>max{A,B,C}
|
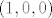 
| Citat: |
2. Zadana je baza b i tri medusobno razlicite znamenke sustava s bazom b kojima je suma jednaka b-1 i od kojih niti jedna nije 0. Promatramo sumu svih brojeva kojima se zapis u bazi b sastoji od tri zadane znamenke. Odredte sve baze b za koje je ta suma veca od 1000 i manja od 2000? |
Pretpostavimo da imamo bazu  i sve takve triplete i sve takve triplete 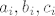 . Vidljivo je da je . Vidljivo je da je  , jer je namanji triplet koji zadovoljava trazeno svojstvo , jer je namanji triplet koji zadovoljava trazeno svojstvo 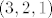 . .
BSOMP da vrijedi 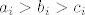 Poredajmo te brojeve kao sumu Poredajmo te brojeve kao sumu
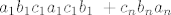
U svakom stupcu se za svaki  svaki od svaki od 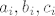 pojavljuje tocno dvaput, pa je suma svakog stupca jednaka (jer je pojavljuje tocno dvaput, pa je suma svakog stupca jednaka (jer je 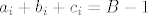 ) )
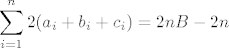
Suma je onda jednaka (suma svega skupa)
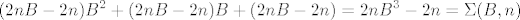
No, ono sto zelimo, jest da je ta suma
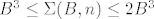
Ako je  veci od veci od  , onda iz , onda iz
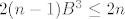 slijedi slijedi 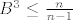 , pa je , pa je  , jer je , jer je 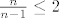 , no to je nemoguce. Dakle, , no to je nemoguce. Dakle, 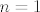 . .
Eh, ali uvjet 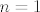 zadovoljavaju samo zadovoljavaju samo  . Za . Za 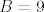 je je 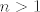 , jer postoje tripleti , jer postoje tripleti 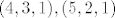 , a za , a za 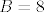 samo samo 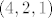 . Sasvim je jasno da . Sasvim je jasno da 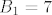 i i 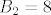 zadovoljavaju trazenu nejednakost, pa je to rjesenje. zadovoljavaju trazenu nejednakost, pa je to rjesenje.
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 19:07 pon, 15. 11. 2004 Naslov: Re: zadatak, dva..? Postano: 19:07 pon, 15. 11. 2004 Naslov: Re: zadatak, dva..? |
    |
|
|
[quote="cinik"][quote="Anonymous"]1. Nadite bar jednu trojku (A,B,C) prirodnih brojeva manjih od 10 t.d. je
broj (A,B,C)b potpuni kvadrat za svaku bazu b ? b>max{A,B,C}
[/quote]
[latex](1,0,0)[/latex] :wink:[/quote]
_Prirodnih_ brojeva, Hans. :-P
(1,6,9) .
| cinik (napisa): | | Anonymous (napisa): | 1. Nadite bar jednu trojku (A,B,C) prirodnih brojeva manjih od 10 t.d. je
broj (A,B,C)b potpuni kvadrat za svaku bazu b ? b>max{A,B,C}
|
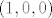  |
_Prirodnih_ brojeva, Hans. 
(1,6,9) .
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 21:01 pon, 15. 11. 2004 Naslov: Re: zadatak, dva..? Postano: 21:01 pon, 15. 11. 2004 Naslov: Re: zadatak, dva..? |
    |
|
|
[quote="cinik"][quote="veky"]
_Prirodnih_ brojeva, Hans. :-P
[/quote]
Od kada, molim te, nula nije prirodni broj? I to jos u racunrastvu?![/quote]
Oduvijek, u hrvatskom jeziku. Nažalost, slažem se, ali je tako.
| cinik (napisa): | | veky (napisa): |
_Prirodnih_ brojeva, Hans. 
|
Od kada, molim te, nula nije prirodni broj? I to jos u racunrastvu?! |
Oduvijek, u hrvatskom jeziku. Nažalost, slažem se, ali je tako.
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
|






