| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Hrvatski Bog Mars
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Crni
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Hrvatski Bog Mars
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 10:46 ned, 16. 4. 2006 Naslov: Postano: 10:46 ned, 16. 4. 2006 Naslov: |
    |
|
|
Ne, takav prsten ne mora biti komutativan.
Iz uvjeta je jasno da vrijedi
(ab - ba)^2 = 0,
znači hoćemo da komutator ne mora biti jednak 0, ali da mu je kvadrat
jednak 0.
Uzmimo kvadratne matrice reda 2 kojima je drugi redak jednak 0.
One čine prsten, nekomutativan, a komutator ima 0 na sva tri mjesta
osim (1,2) pa mu je kvadrat nulmatrica.
Uz improviziranu pjesmicu:
Tko previše sluša abbu,
pretvori se sam u .... :D !
(Gost, nekrležijanski)
Ne, takav prsten ne mora biti komutativan.
Iz uvjeta je jasno da vrijedi
(ab - ba)^2 = 0,
znači hoćemo da komutator ne mora biti jednak 0, ali da mu je kvadrat
jednak 0.
Uzmimo kvadratne matrice reda 2 kojima je drugi redak jednak 0.
One čine prsten, nekomutativan, a komutator ima 0 na sva tri mjesta
osim (1,2) pa mu je kvadrat nulmatrica.
Uz improviziranu pjesmicu:
Tko previše sluša abbu,
pretvori se sam u ....  ! !
(Gost, nekrležijanski)
|
|
| [Vrh] |
|
Dr. Phil. Leone Glembay
Gost
|
 Postano: 11:39 ned, 16. 4. 2006 Naslov: Postano: 11:39 ned, 16. 4. 2006 Naslov: |
    |
|
|
Ne slušaj Hrvatskog Boga Marsa, on ovijek tera po svome, a to pitanje nas uopce ne zanima. Ono što nas krležijanske likove muči muči je slijedeći zadatak:
Neka je [latex](G, \cdot)[/latex] grupa i pretpostavimo da je [latex]\circ : G \times G \rightarrow G[/latex] asocijativna binarna operacija sa svojstvom da je za svako [latex]g,h \in G[/latex] produkt [latex]g \circ h\in \{g \cdot h, h \cdot g \}[/latex]. Dokažite da je tada nužno [latex]\circ = \cdot[/latex], tj. da vrijedi [latex]g \circ h= g \cdot h[/latex] za sve [latex]g,h \in G[/latex].
Hvala!
P.s. Pozdravlja vas i Barunica Castelli-Glembay.
Ne slušaj Hrvatskog Boga Marsa, on ovijek tera po svome, a to pitanje nas uopce ne zanima. Ono što nas krležijanske likove muči muči je slijedeći zadatak:
Neka je 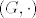 grupa i pretpostavimo da je grupa i pretpostavimo da je 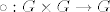 asocijativna binarna operacija sa svojstvom da je za svako asocijativna binarna operacija sa svojstvom da je za svako 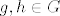 produkt produkt 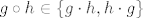 . Dokažite da je tada nužno . Dokažite da je tada nužno  , tj. da vrijedi , tj. da vrijedi 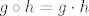 za sve za sve 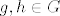 . .
Hvala!
P.s. Pozdravlja vas i Barunica Castelli-Glembay.
|
|
| [Vrh] |
|
Dr. Phil. Leone Glembay
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Filip Latinovicz
Gost
|
 Postano: 13:10 ned, 16. 4. 2006 Naslov: Postano: 13:10 ned, 16. 4. 2006 Naslov: |
    |
|
|
[quote="gost"]Uzmimo kvadratne matrice reda 2 kojima je drugi redak jednak 0.[/quote]
Lijepo, to je dobar primjer. Jedino sto bi ipak trebalo provjeriti da u tom prstenu vrijedi abba=baba, a ne samo (ab-ba)^2=0. Ali to je vrlo jednostavno za provesti. Pohvaljujem naseg gosta.
Ima i drugih zgodnih primjera, npr. 3x3 (ili pak 4x4) realne matrice koje imaju nule na glavnoj dijagonali i ispod nje.
P.S. Daj Balocanski dodji vise na tu cugu, pa nije svaki dan Uskrs.
Cestitam Uskrs i svojim prijateljima Glembajevima, ljubim ruke milostiva.
P.P.S. Glasujte za [color=red]smirivanje napornih asistenata[/color]!
[color=darkred][b]Edit by vsego.[/b][/color] :evil:
| gost (napisa): | | Uzmimo kvadratne matrice reda 2 kojima je drugi redak jednak 0. |
Lijepo, to je dobar primjer. Jedino sto bi ipak trebalo provjeriti da u tom prstenu vrijedi abba=baba, a ne samo (ab-ba)^2=0. Ali to je vrlo jednostavno za provesti. Pohvaljujem naseg gosta.
Ima i drugih zgodnih primjera, npr. 3x3 (ili pak 4x4) realne matrice koje imaju nule na glavnoj dijagonali i ispod nje.
P.S. Daj Balocanski dodji vise na tu cugu, pa nije svaki dan Uskrs.
Cestitam Uskrs i svojim prijateljima Glembajevima, ljubim ruke milostiva.
P.P.S. Glasujte za smirivanje napornih asistenata!
Edit by vsego. 
|
|
| [Vrh] |
|
|







