|
Molio bih nekoga ako mi može objasniti jedan dokaz osnovnog teorema algebre iz knjige "Elementarna matematika 1". I molio bih što detaljnije odgovore, jer te stvari stvarno ne kužim.
Najprije ću navesti jednu lemu, koja se spominje u dokazu, i njen dokaz.
[b]Lema: (o modulu najstarijeg člana)[/b]
Neka je [latex]f(z)=a_0z^n+a_1z^{n-1}+\cdots+a_{n-1}z+a_n[/latex] polinom stupnja [latex]n\geq 1[/latex] s kompleksnim koeficijentima. Tada postoji pozitivan broj [latex]r \in \mathbb{R}[/latex] takav da vrijedi
[latex]|z|>r \Rightarrow |a_0z^n|>|a_1z^{n-1}+\cdots+a_{n-1}+a_n|[/latex].
[b]Dokaz leme:[/b] Stavimo [latex]M=max\{|a_1|,\ldots,|a_n|\}[/latex] i [latex]r=\frac{M}{|a_0|}+1[/latex]. Ako je [latex]|z|>r \leq 1[/latex], onda slijedi da je [latex]|a_0|>\frac{M}{|z|-1}[/latex]. Odavde, zbog pravila za računanje s modulima kompleksnih brojeva, imamo da je za [latex]|z|>r[/latex]:
[latex]\displaystyle|a_0z^n|=|a_0||z^n|>\frac{M|z|^n}{|z|-1}>\frac{M(|z|^n-1)}{|z|-1}=M(|z|^{n-1}+\cdots+|z|+1)\geq\\
\geq|a_1||z|^{n-1}+\cdots+|a_{n-1}||z|+|a_n|=|a_1z^{n-1}|+\cdots+|a_{n-1}z|+|a_0|\geq\\
\geq|a_1z^{n-1}+\cdots+a_{n-1}z+a_1|[/latex].
To kužim, ali tek sad idem na teorem.
[b]Teorem: (osnovni teorem algebre)[/b]
Svaki polinom
[latex]f(z)=a_nz^n+a_{n-1}z^{n-1}+\cdots+a_1z+a_0[/latex]
stupnja [latex]n\geq1[/latex] s kompleksnim koeficijentima ima nultočku u [latex]\mathbb{C}[/latex].
[b]Skica dokaza:[/b] Možemo očito pretpostaviti da je [latex]a_n=1[/latex]. Neka je [latex]\displaystyle\mu=\inf_{z\in\mathbb{C}}|f(z)|[/latex]. Kako je [latex]\displaystyle f(z)=z^n\bigg[1+\frac{a_{n-1}}{z}+\cdots+\frac{a_0}{z^n}\bigg][/latex], to je
[latex]\displaystyle|f(z)|\geq|z|^n\bigg[1-\frac{|a_{n-1}|}{|z|}-\cdots-\frac{|a_0|}{|z|^n}\bigg][/latex].
Slično kao u dokazu Leme slijedi da postoji realan broj [latex]R>0[/latex], tako da [latex]|z|>R[/latex] povlači [latex]|f(z)|>max\{1,2\mu\}[/latex] [i][color=red](Ovo ne kužim, zašto 1 i [latex]2\mu[/latex]? Po čemu to vidimo?)[/color][/i]. Odavde i iz definicije infimuma slijedi da postoji niz točaka [latex](z_k)[/latex] u krugu [latex]|z|\leq R[/latex] tako da je [latex]0<|f(z_k)|-\mu<\frac{1}{k},k\in\mathbb{N}[/latex].
Dokažimo da u [latex]\mathbb{C}[/latex] (zapravo već u tom krugu) postoji točka [latex]z_0[/latex] za koju je [latex]|f(z_0)|=\mu[/latex]. Neka je [latex]z_k=x_k+iy_k,k\in\mathbb{N}[/latex]. Tada je [latex]max\{|x_k|,|y_k|\}\leq|z_k|\leq R[/latex], pa su nizovi realnih brojeva [latex](x_k)[/latex] i [latex](y_k)[/latex] omeđeni. No, svaki omeđeni niz ima konvergentni podniz. Stoga, neka je [latex]\displaystyle(x_{k_l})[/latex] konvergentni podniz od [latex](x_k)[/latex], pa onda neka je [latex]\displaystyle(y_{k_{l_m}})[/latex] konvergentni podniz od [latex]\displaystyle(y_{k_l})[/latex]. Tako dobivamo konvergentni niz kompleksnih brojeva[latex]\displaystyle z_{k_{l_m}}=x_{k_{l_m}}+iy_{k_{l_m}}[/latex], čiji je limes [latex]\displaystyle\lim_{m\to\infty}z_{k_{l_m}}=\lim_{m\to\infty}x_{k_{l_m}}+i\lim_{m\to\infty}y_{k_{l_m}}=x_0+iy_0=z_0[/latex]. Budući da je [latex]|z_k|\to|z_0|[/latex] kada [latex]k\to\infty[/latex], slijedi da je [latex]|z_0|\leq R[/latex]. Da izbjegnemo nepotrebne trostruke indekse, možemo pretpostaviti da već sam niz [latex](z_k)[/latex] konvergira. Kako je polinom [latex]f(z)[/latex] neprekidan u točki [latex]z_0\in\mathbb{C}[/latex], slijedi da je [latex]\displaystyle\lim_{k\to\infty}f(z_k)=f(z_0)[/latex]. No tada slijedi da je [latex]\displaystyle|f(z_0)|=\lim_{k\to\infty}|f(z_k)|=\mu[/latex] [i][color=red](To sve recimo da kužim)[/color][/i].
Dokažimo da je [latex]\mu=0[/latex]. Pretpostavimo suprotno, da je [latex]\mu>0[/latex]. Kako je [latex]f(z_0)\neq 0[/latex], to je [latex]\displaystyle g(z)=\frac{f(z+z_0)}{f(z_0)}[/latex] polinom n-tog stupnja. Očito je [latex]g(0)=1[/latex] i kako se u točki [latex]z_0[/latex] dostiže infimum od [latex]|f(z)|[/latex], slijedi da je [latex]\displaystyle|g(z)|=\frac{|f(z+z_0)|}{|f(z_0)|}\geq 1[/latex]. Zbog [latex]g(0)=1[/latex], polinom [latex]g(z)[/latex] je oblika
[latex]g(z)=1+b_kz^k+b_{k+1}z^{k+1}+\cdots+b_nz^n[/latex],
gdje je [latex]|b_k|\neq 0[/latex] i [latex]1\leq k\leq n[/latex]. Neka je [latex]b_k=\rho e^{i\psi}[/latex] [i][color=red](Ovakav zapis kompleksnih brojeva uopće ne kužim. Kakve e ima veze? Ako bi i to netko mogao malo pojasniti.)[/color][/i] i neka je [latex]\varphi=\frac{\pi-\psi}{k}[/latex]. Tada je [latex]b_k\cdot(e^{i\varphi})^k=\rho e^{i\psi}e^{i(\pi-\psi)}=\rho e^{i\pi}=-\rho=-|b_k|[/latex] [i][color=red](Ove zadnje dvije jednakosti ne kužim kako smo dobili.)[/color][/i]. Neka je sada [latex]z=re^{i\varphi}[/latex]. Tada imamo
[latex]|g(re^{i\varphi})|\leq|1+b_kz^k|+(|b_{k+1}z^{k+1}|+\cdots+|b_nz^n|)=\\
=|1-r^k|b_k||+r^{k+1}(|b_{k+1}|+\cdots+|b_n|r^{n-k-1})=\\
=1-r^k(|b_k|-r|b_{k+1}|-\cdots-r^{n-k}|b_n|)<1[/latex],
[i][color=red](Zašto su u drugom redu od z-ova ostali samo r-ovi?)[/color][/i] gdje je [latex]r>0[/latex] dovoljno mali broj. No [latex]|g(z)|\geq 1[/latex] za [latex]z\in\mathbb{C}[/latex]. To je kontradikcija, pa slijedi da je [latex]\mu=0[/latex], te stoga [latex]f(z_0)=0[/latex].
Eto, znam da toga ima dosta i da gnjavim, ali kad sam se već potrudio kolko-tolko svladati LATEX... 8)
Molio bih nekoga ako mi može objasniti jedan dokaz osnovnog teorema algebre iz knjige "Elementarna matematika 1". I molio bih što detaljnije odgovore, jer te stvari stvarno ne kužim.
Najprije ću navesti jednu lemu, koja se spominje u dokazu, i njen dokaz.
Lema: (o modulu najstarijeg člana)
Neka je 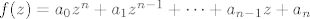 polinom stupnja polinom stupnja 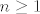 s kompleksnim koeficijentima. Tada postoji pozitivan broj s kompleksnim koeficijentima. Tada postoji pozitivan broj 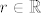 takav da vrijedi takav da vrijedi
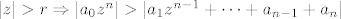 . .
Dokaz leme: Stavimo 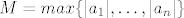 i i 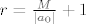 . Ako je . Ako je 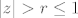 , onda slijedi da je , onda slijedi da je 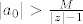 . Odavde, zbog pravila za računanje s modulima kompleksnih brojeva, imamo da je za . Odavde, zbog pravila za računanje s modulima kompleksnih brojeva, imamo da je za  : :
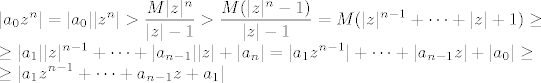 . .
To kužim, ali tek sad idem na teorem.
Teorem: (osnovni teorem algebre)
Svaki polinom
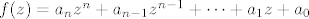
stupnja 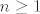 s kompleksnim koeficijentima ima nultočku u s kompleksnim koeficijentima ima nultočku u  . .
Skica dokaza: Možemo očito pretpostaviti da je 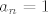 . Neka je . Neka je 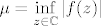 . Kako je . Kako je 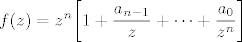 , to je , to je
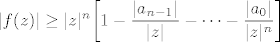 . .
Slično kao u dokazu Leme slijedi da postoji realan broj 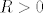 , tako da , tako da 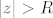 povlači povlači 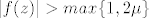 (Ovo ne kužim, zašto 1 i (Ovo ne kužim, zašto 1 i 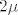 ? Po čemu to vidimo?). Odavde i iz definicije infimuma slijedi da postoji niz točaka ? Po čemu to vidimo?). Odavde i iz definicije infimuma slijedi da postoji niz točaka 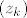 u krugu u krugu 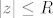 tako da je tako da je 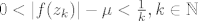 . .
Dokažimo da u  (zapravo već u tom krugu) postoji točka (zapravo već u tom krugu) postoji točka 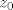 za koju je za koju je 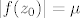 . Neka je . Neka je 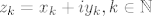 . Tada je . Tada je 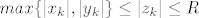 , pa su nizovi realnih brojeva , pa su nizovi realnih brojeva 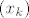 i i 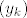 omeđeni. No, svaki omeđeni niz ima konvergentni podniz. Stoga, neka je omeđeni. No, svaki omeđeni niz ima konvergentni podniz. Stoga, neka je 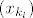 konvergentni podniz od konvergentni podniz od 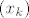 , pa onda neka je , pa onda neka je 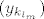 konvergentni podniz od konvergentni podniz od 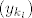 . Tako dobivamo konvergentni niz kompleksnih brojeva . Tako dobivamo konvergentni niz kompleksnih brojeva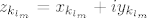 , čiji je limes , čiji je limes 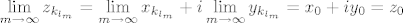 . Budući da je . Budući da je 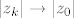 kada kada 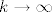 , slijedi da je , slijedi da je  . Da izbjegnemo nepotrebne trostruke indekse, možemo pretpostaviti da već sam niz . Da izbjegnemo nepotrebne trostruke indekse, možemo pretpostaviti da već sam niz 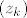 konvergira. Kako je polinom konvergira. Kako je polinom 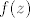 neprekidan u točki neprekidan u točki 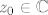 , slijedi da je , slijedi da je 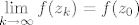 . No tada slijedi da je . No tada slijedi da je 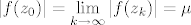 (To sve recimo da kužim). (To sve recimo da kužim).
Dokažimo da je 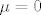 . Pretpostavimo suprotno, da je . Pretpostavimo suprotno, da je 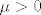 . Kako je . Kako je 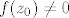 , to je , to je 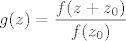 polinom n-tog stupnja. Očito je polinom n-tog stupnja. Očito je 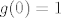 i kako se u točki i kako se u točki 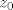 dostiže infimum od dostiže infimum od 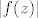 , slijedi da je , slijedi da je 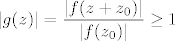 . Zbog . Zbog 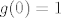 , polinom , polinom 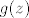 je oblika je oblika
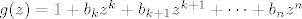 , ,
gdje je 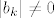 i i 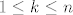 . Neka je . Neka je 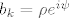 (Ovakav zapis kompleksnih brojeva uopće ne kužim. Kakve e ima veze? Ako bi i to netko mogao malo pojasniti.) i neka je (Ovakav zapis kompleksnih brojeva uopće ne kužim. Kakve e ima veze? Ako bi i to netko mogao malo pojasniti.) i neka je 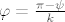 . Tada je . Tada je 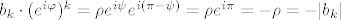 (Ove zadnje dvije jednakosti ne kužim kako smo dobili.). Neka je sada (Ove zadnje dvije jednakosti ne kužim kako smo dobili.). Neka je sada 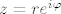 . Tada imamo . Tada imamo
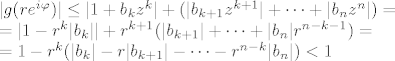 , ,
(Zašto su u drugom redu od z-ova ostali samo r-ovi?) gdje je 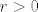 dovoljno mali broj. No dovoljno mali broj. No 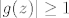 za za 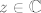 . To je kontradikcija, pa slijedi da je . To je kontradikcija, pa slijedi da je 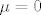 , te stoga , te stoga 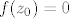 . .
Eto, znam da toga ima dosta i da gnjavim, ali kad sam se već potrudio kolko-tolko svladati LATEX... 
|





