|
[quote="jecika"]1.Izracunati lim kad n tezi beskonacno od n*(e-(1+1/n)na n).
2.Izracunati integral granica od - beskonacno do + beskonacno od e na arctan 1/2*(x-1/x) sve to kroz 1+x na 2 dx.[/quote]
Bok jecika. Zavodu se svidio prvi zadatak. Kako si ti? Evo rješenja.
1. [latex]L:=\lim_{n \rightarrow \infty} n \cdot(e-(1+\frac{1}{n})^n)=\frac{e}{2}[/latex].
Ajmo to recimo dokazati ovako:
Najprije primijetimo da je [latex]L= \lim_{x \rightarrow 0} \frac{1}{x} \cdot(e-(1+x)^\frac{1}{x})[/latex] i stavimo [latex]f(x):=(1+x)^\frac{1}{x}[/latex]. Kako je [latex]\lim_{x \rightarrow 0}f(x)=e[/latex], prema L'Hospitalovom pravilu je
[latex]L=\frac{e-f(x)}{x}=\lim_{x \rightarrow 0} -f'(x)[/latex]. Imamo [latex]f'(x)=f(x)\cdot \Big[-\frac{1}{x^2}\ln(1+x)]+ \frac{1}{x}\cdot \frac{1}{1+x}\Big][/latex] (logaritamska derivacija) i stavimo [latex]G:=\lim_{x \rightarrow 0}\Big[-\frac{1}{x^2}\ln(1+x)+ \frac{1}{x}\cdot \frac{1}{1+x}\Big]=\lim_{x \rightarrow 0}\frac{-\frac{1}{x}\ln(1+x)+ \cdot \frac{1}{1+x}}{x}[/latex].
Ponovo koristeci L'H pravilo imamo [latex]G=\lim_{x \rightarrow 0} \Big[ -\frac{1}{(1+x)^2} + \frac{1}{x^2}\ln(1+x)-\frac{1}{x}\cdot\frac{1}{1+x} \Big][/latex][latex]=\lim_{x \rightarrow 0}\Big[-\frac{1}{(1+x)^2} + \frac{1}{x} \cdot (\frac{1}{x} \ln(1+x )- \frac{1}{1+x})\Big][/latex].
Primijetimo da je limes desnog sumanda jednak [latex]-G[/latex], pa je gornji limes jednak [latex]-1-G[/latex]. Znači imamo jednadžbu [latex]G=-1-G[/latex], dakle [latex]G=-\frac{1}{2}[/latex].
I na kraju, imamo [latex]L=-\lim_{x \rightarrow 0}f(x)\cdot \Big[-\frac{1}{x^2}\ln(1+x)]+ \frac{1}{x}\cdot \frac{1}{1+x}\Big]=-e \cdot \frac{-1}{2}=\frac{e}{2}[/latex] i to je to.
2. A ovaj integral baš i ne liči na neki koji bi konvergirao. :wc:
Lijepi pozdrav dr. Exodusu :drinking: i dijelu zavoda iz dijaspore :changes:
| jecika (napisa): | 1.Izracunati lim kad n tezi beskonacno od n*(e-(1+1/n)na n).
2.Izracunati integral granica od - beskonacno do + beskonacno od e na arctan 1/2*(x-1/x) sve to kroz 1+x na 2 dx. |
Bok jecika. Zavodu se svidio prvi zadatak. Kako si ti? Evo rješenja.
1. 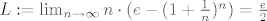 . .
Ajmo to recimo dokazati ovako:
Najprije primijetimo da je 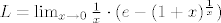 i stavimo i stavimo 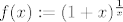 . Kako je . Kako je 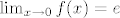 , prema L'Hospitalovom pravilu je , prema L'Hospitalovom pravilu je
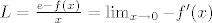 . Imamo . Imamo 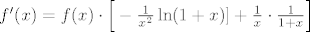 (logaritamska derivacija) i stavimo (logaritamska derivacija) i stavimo 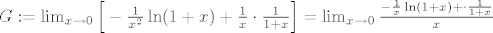 . .
Ponovo koristeci L'H pravilo imamo 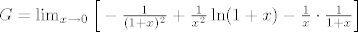 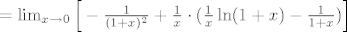 . .
Primijetimo da je limes desnog sumanda jednak 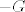 , pa je gornji limes jednak , pa je gornji limes jednak 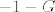 . Znači imamo jednadžbu . Znači imamo jednadžbu 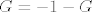 , dakle , dakle 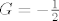 . .
I na kraju, imamo 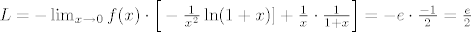 i to je to. i to je to.
2. A ovaj integral baš i ne liči na neki koji bi konvergirao. 
Lijepi pozdrav dr. Exodusu  i dijelu zavoda iz dijaspore i dijelu zavoda iz dijaspore 
_________________  |





