| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 16:30 ned, 24. 9. 2006 Naslov: Fourierov red teorija Postano: 16:30 ned, 24. 9. 2006 Naslov: Fourierov red teorija |
    |
|
|
Dakle, poznate su mi sljedeće stvari:
I)
Ako niz funkcija (u_n) ima svojstvo da je l u_n(x) l<=a_n za svaki n prirodan i x iz I, te ako je sum(n=1, +inf)(a_n)<+inf tada red funkcija
sum(n=1, +inf)(u_n) uniformno konvergira. (Wierstrassov teorem)
II)
Ako niz funkcija (f_n) uniformno konvergira prema f i ako za svaki prirodni n vrijedi da je f_n neprekidna, tada je i f neprekidna. (uniformna konvergencija čuva neprekidnost)
III)
Ako za svaki prirodni n vrijedi da je u_n neprekidna na segmentu I=[a,b] i da red funkcija sum(n=1, +inf)(u_n) uniformno konvergira prema f na I tada vrijedi:
i) za svaki x iz I postoji (integral od a do x)(f(t)dt) i vrijedi da je
(integral od a do x)(f(t)dt)=
=sum(n=1,+inf)((integral od a do x)(u_n(t)dt)) (integral sume je suma integrala)
ii) red funkcija sum(n=1,+inf)(U_n), gdje je
U_n(x):=(integral od a do x)(u_n(t)dt), uniformno konvergira prema F(x):=(integral od a do x)(f(t)dt).
IV)
Ako za svaki prirodni n vrijedi da je u_n neprekidna na segmentu I, da red funkcija sum(n=1,+inf)(u_n) uniformno konvergira prema f na I i da red funkcija sum(n=1,+inf)(u'_n) uniformno konvergira prema g na I, tada je f'=g (derivacija sume je suma derivacija).
E sad, imamo onaj lijepi fourierov red funkcije f, (a_0)/2+ sum... itd. i pitamo se da li on ima ikakve veze sa f.
Sigurno znamo da se red sastoji od beskonačno diferencijabilnih funkcija, znači i neprekidnih, i pretpostavimo da je f neprekidna, znači i (R)-integrabilna. Da bi našli koeficijente a_0, a_1... i b_1, b_2... moramo integrirati od -pi do pi pa želimo ubaciti integral pod beskonačnu sumu, a za to nam treba III), posebno, želimo znati da li fourierov red funkcije f uniformno konvergira, jer je u_n:=sin(nx)*a_n+cos(nx)*b_n neprekidna za svaki n prirodan, a da bismo provjerili da li fourierov red uniformno konvergira, valjda trebamo koristiti I). Mene sad zanima, kak? Tek računamo koeficijente, još ne znamo kak red izgleda, a već bi trebali reć da li uniformno konvergira prije nego nađemo koeficijente, malo me to zbunjuje. Ak neko može dovršit priču koristeći I) - IV) o tome kad je f(x)= fourierovom redu od f, puno mu hvala.
Dakle, poznate su mi sljedeće stvari:
I)
Ako niz funkcija (u_n) ima svojstvo da je l u_n(x) l⇐a_n za svaki n prirodan i x iz I, te ako je sum(n=1, +inf)(a_n)<+inf tada red funkcija
sum(n=1, +inf)(u_n) uniformno konvergira. (Wierstrassov teorem)
II)
Ako niz funkcija (f_n) uniformno konvergira prema f i ako za svaki prirodni n vrijedi da je f_n neprekidna, tada je i f neprekidna. (uniformna konvergencija čuva neprekidnost)
III)
Ako za svaki prirodni n vrijedi da je u_n neprekidna na segmentu I=[a,b] i da red funkcija sum(n=1, +inf)(u_n) uniformno konvergira prema f na I tada vrijedi:
i) za svaki x iz I postoji (integral od a do x)(f(t)dt) i vrijedi da je
(integral od a do x)(f(t)dt)=
=sum(n=1,+inf)((integral od a do x)(u_n(t)dt)) (integral sume je suma integrala)
ii) red funkcija sum(n=1,+inf)(U_n), gdje je
U_n(x):=(integral od a do x)(u_n(t)dt), uniformno konvergira prema F(x):=(integral od a do x)(f(t)dt).
IV)
Ako za svaki prirodni n vrijedi da je u_n neprekidna na segmentu I, da red funkcija sum(n=1,+inf)(u_n) uniformno konvergira prema f na I i da red funkcija sum(n=1,+inf)(u'_n) uniformno konvergira prema g na I, tada je f'=g (derivacija sume je suma derivacija).
E sad, imamo onaj lijepi fourierov red funkcije f, (a_0)/2+ sum... itd. i pitamo se da li on ima ikakve veze sa f.
Sigurno znamo da se red sastoji od beskonačno diferencijabilnih funkcija, znači i neprekidnih, i pretpostavimo da je f neprekidna, znači i (R)-integrabilna. Da bi našli koeficijente a_0, a_1... i b_1, b_2... moramo integrirati od -pi do pi pa želimo ubaciti integral pod beskonačnu sumu, a za to nam treba III), posebno, želimo znati da li fourierov red funkcije f uniformno konvergira, jer je u_n:=sin(nx)*a_n+cos(nx)*b_n neprekidna za svaki n prirodan, a da bismo provjerili da li fourierov red uniformno konvergira, valjda trebamo koristiti I). Mene sad zanima, kak? Tek računamo koeficijente, još ne znamo kak red izgleda, a već bi trebali reć da li uniformno konvergira prije nego nađemo koeficijente, malo me to zbunjuje. Ak neko može dovršit priču koristeći I) - IV) o tome kad je f(x)= fourierovom redu od f, puno mu hvala.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 23:51 pon, 25. 9. 2006 Naslov: Re: Fourierov red teorija Postano: 23:51 pon, 25. 9. 2006 Naslov: Re: Fourierov red teorija |
    |
|
|
[quote="alen"]Dakle, poznate su mi sljedeće stvari:
I)
Ako niz funkcija (u_n) ima svojstvo da je l u_n(x) l<=a_n za svaki n prirodan i x iz I, te ako je sum(n=1, +inf)(a_n)<+inf tada red funkcija
sum(n=1, +inf)(u_n) uniformno konvergira. (Wierstrassov teorem)
II)
Ako niz funkcija (f_n) uniformno konvergira prema f i ako za svaki prirodni n vrijedi da je f_n neprekidna, tada je i f neprekidna. (uniformna konvergencija čuva neprekidnost)
III)
Ako za svaki prirodni n vrijedi da je u_n neprekidna na segmentu I=[a,b] i da red funkcija sum(n=1, +inf)(u_n) uniformno konvergira prema f na I tada vrijedi:
i) za svaki x iz I postoji (integral od a do x)(f(t)dt) i vrijedi da je
(integral od a do x)(f(t)dt)=
=sum(n=1,+inf)((integral od a do x)(u_n(t)dt)) (integral sume je suma integrala)
ii) red funkcija sum(n=1,+inf)(U_n), gdje je
U_n(x):=(integral od a do x)(u_n(t)dt), uniformno konvergira prema F(x):=(integral od a do x)(f(t)dt).
IV)
Ako za svaki prirodni n vrijedi da je u_n neprekidna na segmentu I, da red funkcija sum(n=1,+inf)(u_n) uniformno konvergira prema f na I i da red funkcija sum(n=1,+inf)(u'_n) uniformno konvergira prema g na I, tada je f'=g (derivacija sume je suma derivacija).
E sad, imamo onaj lijepi fourierov red funkcije f, (a_0)/2+ sum... itd. i pitamo se da li on ima ikakve veze sa f.
Sigurno znamo da se red sastoji od beskonačno diferencijabilnih funkcija, znači i neprekidnih, i pretpostavimo da je f neprekidna, znači i (R)-integrabilna. Da bi našli koeficijente a_0, a_1... i b_1, b_2... moramo integrirati od -pi do pi pa želimo ubaciti integral pod beskonačnu sumu, a za to nam treba III), posebno, želimo znati da li fourierov red funkcije f uniformno konvergira, jer je u_n:=sin(nx)*a_n+cos(nx)*b_n neprekidna za svaki n prirodan, a da bismo provjerili da li fourierov red uniformno konvergira, valjda trebamo koristiti I). Mene sad zanima, kak? Tek računamo koeficijente, još ne znamo kak red izgleda, a već bi trebali reć da li uniformno konvergira prije nego nađemo koeficijente, malo me to zbunjuje. Ak neko može dovršit priču koristeći I) - IV) o tome kad je f(x)= fourierovom redu od f, puno mu hvala.[/quote]
Nisam 100% siguran da sam točno shvatio što ti nije jasno, no napisat ću ti neke natuknice vezane uz problem točkovne konvergencije Fourierovog reda dane funkcije
Ako je npr. [latex]f \in C([0,1\rangle)[/latex] ograničena funkcija, tada njoj pridružiemo n-te simetrične parcijalne sume [latex](S_n f)_{n \geq 0}[/latex] njenog Fourierovog reda, definirane s [latex]S_n f (x):= \sum_{m=-n}^{n}c_m e^{2\pi i m x}[/latex], gdje su koeficijenti [latex](c_m)_{m \in \mathbb{Z}}[/latex] dani s [latex]c_m:=\int_{0}^{1} f(x) e^{-2 \pi i m x} dx [/latex].
Zasad nemamo pojma da li taj niz parcijalnih suma [latex](S_n f)_{n \geq 0}[/latex] uopće konvergira po točkama i ukoliko konvergira, da li mu je suma baš početna funkcija [latex]f[/latex].
Uzmimo npr. slučaj kada su koeficijenti [latex](c_m)_{m \in \mathbb{Z}}[/latex] sumabilni, tj. kada vrijedi da je [latex]\sum_{m=-\infty}^{\infty}|c_m| < \infty[/latex]. Tada prema Weierstrassovom M-kriteriju znamo da niz parcijalnih suma [latex](S_n f)_{n \geq 0}[/latex] svakako uniformno konvergira (budući su funkcije [latex]x \mapsto e^{2 \pi i m x}[/latex] po modulu jednake 1 u svakoj točki [latex]x \in [0,1\rangle[/latex]). Znači suma tog reda je nekakva neprekidna funkcija, no još ne znamo da li mu je suma baš [latex]f[/latex]. No ne vidim kako bi i u tom jednostavnom slučaju to mogao dokazati koristeći samo teoreme koje si naveo, no to svakako možemo dokazati koristeći neke rezultate teorije mjere, ili koristeći neke rezultate iz parcijalnih diferencijalnih jednadžbi vezanih uz Poissonovu jezgru (za koje pretpostavljam da još uvijek ne znaš).
Znači proces ide tako da najprije izračunaš (odn. ocijeniš) F-koeficijente dane funkcije, onda koristeći neke rezultate ispitaš da li niz parcijalnih suma [latex](S_n f)_{n \geq 0}[/latex] uopće konvergira (točkovno ili uniformno) te, ukoliko je odgovor pozitivan, ostaje ispitati kakve njihov limes [latex]\lim_n S_n f[/latex] ima veze sa [latex]f[/latex] i to je (kao što rekoh) općenito dosta netrivijalno (npr. postoji rezultat od [b]du Bois Reymonda[/b] koji kaže da postoji neprekidna i ograničena funkcija [latex]f \in C([0, 1\rangle)[/latex] za koju niz [latex](S_n f(x))_{n \geq 0}[/latex] divergira u nekoj točki [latex]x \in [0,1 \rangle[/latex].
Jedan od poznatijih teorema koji nam daje odgovor na pitanje točkovne konvergencije F-reda je tzv. [b]Dirichletov teorem[/b] koji kaže: Ako je [latex]f[/latex] po dijelovima neprekidna, ograničena i po dijelovima monotona funkcija na [latex][0,1 \rangle[/latex], tada niz F-parc suma [latex](S_n f)_{n \geq 0}[/latex] točkovno konvergira, s [latex]\lim _n S_n f(x)= \frac{1}{2}[ f(x+)+f(x-)][/latex].
Također, postoje i drugi načini sumabilnosti F-parcijalih suma dane funkcije uz koje će taj red konvergirati prema toj funkciji. Jedan od poznatijih načina sumabilnosti je [b]sumabilnost u smislu Cesara[/b], a to imaš obrađeno u knjizi prof. Kurepe: Matematička analiza 2.
Ako te još nešto zanima vezano za tu problematiku, preporučio bih ti knjige:
1. J. Duoandikoetxea: Fourier analysis, Graduate studies in mathematics, volume 29, AMS, 2001
2. Y. Katznelson: An intorduction to harmonic analysis, CMP, 2004,
jedino što se za njihovo čitanje pretpostavlja znanje realne analize. :D
| alen (napisa): | Dakle, poznate su mi sljedeće stvari:
I)
Ako niz funkcija (u_n) ima svojstvo da je l u_n(x) l⇐a_n za svaki n prirodan i x iz I, te ako je sum(n=1, +inf)(a_n)<+inf tada red funkcija
sum(n=1, +inf)(u_n) uniformno konvergira. (Wierstrassov teorem)
II)
Ako niz funkcija (f_n) uniformno konvergira prema f i ako za svaki prirodni n vrijedi da je f_n neprekidna, tada je i f neprekidna. (uniformna konvergencija čuva neprekidnost)
III)
Ako za svaki prirodni n vrijedi da je u_n neprekidna na segmentu I=[a,b] i da red funkcija sum(n=1, +inf)(u_n) uniformno konvergira prema f na I tada vrijedi:
i) za svaki x iz I postoji (integral od a do x)(f(t)dt) i vrijedi da je
(integral od a do x)(f(t)dt)=
=sum(n=1,+inf)((integral od a do x)(u_n(t)dt)) (integral sume je suma integrala)
ii) red funkcija sum(n=1,+inf)(U_n), gdje je
U_n(x):=(integral od a do x)(u_n(t)dt), uniformno konvergira prema F(x):=(integral od a do x)(f(t)dt).
IV)
Ako za svaki prirodni n vrijedi da je u_n neprekidna na segmentu I, da red funkcija sum(n=1,+inf)(u_n) uniformno konvergira prema f na I i da red funkcija sum(n=1,+inf)(u'_n) uniformno konvergira prema g na I, tada je f'=g (derivacija sume je suma derivacija).
E sad, imamo onaj lijepi fourierov red funkcije f, (a_0)/2+ sum... itd. i pitamo se da li on ima ikakve veze sa f.
Sigurno znamo da se red sastoji od beskonačno diferencijabilnih funkcija, znači i neprekidnih, i pretpostavimo da je f neprekidna, znači i (R)-integrabilna. Da bi našli koeficijente a_0, a_1... i b_1, b_2... moramo integrirati od -pi do pi pa želimo ubaciti integral pod beskonačnu sumu, a za to nam treba III), posebno, želimo znati da li fourierov red funkcije f uniformno konvergira, jer je u_n:=sin(nx)*a_n+cos(nx)*b_n neprekidna za svaki n prirodan, a da bismo provjerili da li fourierov red uniformno konvergira, valjda trebamo koristiti I). Mene sad zanima, kak? Tek računamo koeficijente, još ne znamo kak red izgleda, a već bi trebali reć da li uniformno konvergira prije nego nađemo koeficijente, malo me to zbunjuje. Ak neko može dovršit priču koristeći I) - IV) o tome kad je f(x)= fourierovom redu od f, puno mu hvala. |
Nisam 100% siguran da sam točno shvatio što ti nije jasno, no napisat ću ti neke natuknice vezane uz problem točkovne konvergencije Fourierovog reda dane funkcije
Ako je npr. 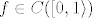 ograničena funkcija, tada njoj pridružiemo n-te simetrične parcijalne sume ograničena funkcija, tada njoj pridružiemo n-te simetrične parcijalne sume 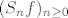 njenog Fourierovog reda, definirane s njenog Fourierovog reda, definirane s 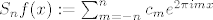 , gdje su koeficijenti , gdje su koeficijenti 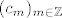 dani s dani s 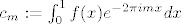 . .
Zasad nemamo pojma da li taj niz parcijalnih suma 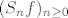 uopće konvergira po točkama i ukoliko konvergira, da li mu je suma baš početna funkcija uopće konvergira po točkama i ukoliko konvergira, da li mu je suma baš početna funkcija  . .
Uzmimo npr. slučaj kada su koeficijenti 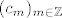 sumabilni, tj. kada vrijedi da je sumabilni, tj. kada vrijedi da je 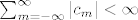 . Tada prema Weierstrassovom M-kriteriju znamo da niz parcijalnih suma . Tada prema Weierstrassovom M-kriteriju znamo da niz parcijalnih suma 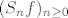 svakako uniformno konvergira (budući su funkcije svakako uniformno konvergira (budući su funkcije 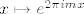 po modulu jednake 1 u svakoj točki po modulu jednake 1 u svakoj točki 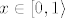 ). Znači suma tog reda je nekakva neprekidna funkcija, no još ne znamo da li mu je suma baš ). Znači suma tog reda je nekakva neprekidna funkcija, no još ne znamo da li mu je suma baš  . No ne vidim kako bi i u tom jednostavnom slučaju to mogao dokazati koristeći samo teoreme koje si naveo, no to svakako možemo dokazati koristeći neke rezultate teorije mjere, ili koristeći neke rezultate iz parcijalnih diferencijalnih jednadžbi vezanih uz Poissonovu jezgru (za koje pretpostavljam da još uvijek ne znaš). . No ne vidim kako bi i u tom jednostavnom slučaju to mogao dokazati koristeći samo teoreme koje si naveo, no to svakako možemo dokazati koristeći neke rezultate teorije mjere, ili koristeći neke rezultate iz parcijalnih diferencijalnih jednadžbi vezanih uz Poissonovu jezgru (za koje pretpostavljam da još uvijek ne znaš).
Znači proces ide tako da najprije izračunaš (odn. ocijeniš) F-koeficijente dane funkcije, onda koristeći neke rezultate ispitaš da li niz parcijalnih suma 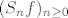 uopće konvergira (točkovno ili uniformno) te, ukoliko je odgovor pozitivan, ostaje ispitati kakve njihov limes uopće konvergira (točkovno ili uniformno) te, ukoliko je odgovor pozitivan, ostaje ispitati kakve njihov limes 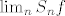 ima veze sa ima veze sa  i to je (kao što rekoh) općenito dosta netrivijalno (npr. postoji rezultat od du Bois Reymonda koji kaže da postoji neprekidna i ograničena funkcija i to je (kao što rekoh) općenito dosta netrivijalno (npr. postoji rezultat od du Bois Reymonda koji kaže da postoji neprekidna i ograničena funkcija 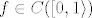 za koju niz za koju niz 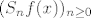 divergira u nekoj točki divergira u nekoj točki 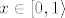 . .
Jedan od poznatijih teorema koji nam daje odgovor na pitanje točkovne konvergencije F-reda je tzv. Dirichletov teorem koji kaže: Ako je  po dijelovima neprekidna, ograničena i po dijelovima monotona funkcija na po dijelovima neprekidna, ograničena i po dijelovima monotona funkcija na 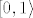 , tada niz F-parc suma , tada niz F-parc suma 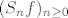 točkovno konvergira, s točkovno konvergira, s 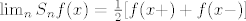 . .
Također, postoje i drugi načini sumabilnosti F-parcijalih suma dane funkcije uz koje će taj red konvergirati prema toj funkciji. Jedan od poznatijih načina sumabilnosti je sumabilnost u smislu Cesara, a to imaš obrađeno u knjizi prof. Kurepe: Matematička analiza 2.
Ako te još nešto zanima vezano za tu problematiku, preporučio bih ti knjige:
1. J. Duoandikoetxea: Fourier analysis, Graduate studies in mathematics, volume 29, AMS, 2001
2. Y. Katznelson: An intorduction to harmonic analysis, CMP, 2004,
jedino što se za njihovo čitanje pretpostavlja znanje realne analize. 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 0:08 uto, 26. 9. 2006 Naslov: Postano: 0:08 uto, 26. 9. 2006 Naslov: |
    |
|
|
Ma Ilja, ti si zakon, baš si se potrudio. Ma, ovo što sam napiso smo radili prošle godine kod prof. Hrvoja, ova 4 teorema su mi se činila ključna da odgovorimo na ona 3 pitanja koja je on postavio (kada fourierov red funkcije f konvergira, u kojem smislu, ima li ikakve veze sa f), a i on jako lijepo to sve ispriča i objasni. Sad sam nedavno primjetio da on na kraju nije povezo te teoreme pa sam krenuo sam to napravit, al bezuspješno. Čini mi se da ipak još nemogu odgovorit na ta pitanja do kraja.
Još jednom hvala, al čini mi se da sam ipak još premali za te stvari.
Ma Ilja, ti si zakon, baš si se potrudio. Ma, ovo što sam napiso smo radili prošle godine kod prof. Hrvoja, ova 4 teorema su mi se činila ključna da odgovorimo na ona 3 pitanja koja je on postavio (kada fourierov red funkcije f konvergira, u kojem smislu, ima li ikakve veze sa f), a i on jako lijepo to sve ispriča i objasni. Sad sam nedavno primjetio da on na kraju nije povezo te teoreme pa sam krenuo sam to napravit, al bezuspješno. Čini mi se da ipak još nemogu odgovorit na ta pitanja do kraja.
Još jednom hvala, al čini mi se da sam ipak još premali za te stvari.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 14:49 uto, 26. 9. 2006 Naslov: Postano: 14:49 uto, 26. 9. 2006 Naslov: |
    |
|
|
Nema problema, super je što si se uopće i upuštao u to, no ipak pričekaj dok naučiš Realnu analizu da se možeš onda u potpunosti pozabaviti Fourierovim redovima, odn. Fourierovom analizom.
Inače, da je naš Vjeko tu, vjerojatno bi ti još bolje odgovorio na tvoje pitanje, budući da Fourierova analiza spada u njegovo područje.
Nema problema, super je što si se uopće i upuštao u to, no ipak pričekaj dok naučiš Realnu analizu da se možeš onda u potpunosti pozabaviti Fourierovim redovima, odn. Fourierovom analizom.
Inače, da je naš Vjeko tu, vjerojatno bi ti još bolje odgovorio na tvoje pitanje, budući da Fourierova analiza spada u njegovo područje.
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 13:22 sub, 7. 10. 2006 Naslov: Postano: 13:22 sub, 7. 10. 2006 Naslov: |
    |
|
|
Dakle, jedan moj dobar prijatelj FERovac (nemojte mu zamjerit, unatoč tome je dobra osoba) mi je postavio pitanje, koje ću ja sad tu napisat. Pitanje je bilo čemu to služi, a baš ne volim ljudima razbijat iluzije o tome kako matematika nije sama sebi cilj i da ona stvarno ima i primjene.
Dakle, radi se o Fourierovom integralu, malo sam pročito njihovu skriptu i skužio sam da služi da bi funkciju koja nije periodična prikazali pomoću harmonika. I sad, kaže tu neki uvjeti: [latex]f:\textbf{R}\rightarrow\textbf{R}[/latex] po dijelovima glatka na svakom konačnom intervalu i apsolutno integrabilna. Onda imam da mi je
[latex]\frac{1}{\pi}\int^{+\infty}_{0}d\lambda\int^{+\infty}_{-\infty}f(\xi)cos\lambda(x-\xi)d\xi=f(x)[/latex] ako je [latex]f[/latex] neprekinuta u [latex]x[/latex] i
[latex]\frac{1}{\pi}\int^{+\infty}_{0}d\lambda\int^{+\infty}_{-\infty}f(\xi)cos\lambda(x-\xi)d\xi=\frac{1}{2}[f(x-0)+f(x+0)][/latex] ako je [latex]x[/latex] točka prekida za [latex]f[/latex].
Iz tog dobiju da je fourierov integral funkcije [latex]f[/latex], [latex]\widetilde{f}=\int^{+\infty}_{0}(A(\lambda)cos\lambda x+B(\lambda)sin\lambda x)d\lambda[/latex], gdje je [latex]A(\lambda)=\frac{1}{\pi}\int^{+\infty}_{-\infty}f(\xi)cos\lambda\xi d\xi[/latex] i [latex]B(\lambda)=\frac{1}{\pi}\int^{+\infty}_{-\infty}f(\xi)sin\lambda\xi d\xi[/latex]
E, i sad primjer, pomoću foureirovog integrala prikaži funkciju
[latex]f\left( x \right) = \left\{ \begin{array}{l}
1,0 < x < 1 \\
\frac{1}{2},x = 0,x = 1 \\
0,x < 0 \vee x > 1 \\
\end{array} \right.[/latex]
Rješenje je [latex]f\left( x \right) = \frac{1}{\pi }\int_0^{ + \infty } {\frac{{\sin \lambda \left( {1 - x} \right) + \sin \lambda x}}{\lambda }d\lambda }[/latex].
I on mene sad pita, zašt ovak lijepu funkciju želim prikazat pomoću ovog nepravog integrala, baš je unakažena (dobro, nije tak reko, bilo je dost psovki) i to ga je jako frustriralo. I nažalost, ja nisam vidio neki razlog zašt to radit. Pouzdajući se u veliku mudrost [latex]Zavoda[/latex] sam to pitanje postavio ovdje uz nadu da će netko (Ilja) odgovorit na njega. Ispričavam se ako sam naporan, to je sve radi imidža matematike kod običnih smrtnika.
Dakle, jedan moj dobar prijatelj FERovac (nemojte mu zamjerit, unatoč tome je dobra osoba) mi je postavio pitanje, koje ću ja sad tu napisat. Pitanje je bilo čemu to služi, a baš ne volim ljudima razbijat iluzije o tome kako matematika nije sama sebi cilj i da ona stvarno ima i primjene.
Dakle, radi se o Fourierovom integralu, malo sam pročito njihovu skriptu i skužio sam da služi da bi funkciju koja nije periodična prikazali pomoću harmonika. I sad, kaže tu neki uvjeti:  po dijelovima glatka na svakom konačnom intervalu i apsolutno integrabilna. Onda imam da mi je po dijelovima glatka na svakom konačnom intervalu i apsolutno integrabilna. Onda imam da mi je
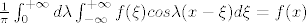 ako je ako je  neprekinuta u neprekinuta u  i i
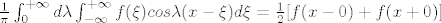 ako je ako je  točka prekida za točka prekida za  . .
Iz tog dobiju da je fourierov integral funkcije  , , 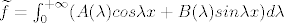 , gdje je , gdje je 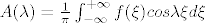 i i 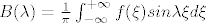
E, i sad primjer, pomoću foureirovog integrala prikaži funkciju
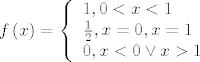
Rješenje je 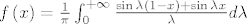 . .
I on mene sad pita, zašt ovak lijepu funkciju želim prikazat pomoću ovog nepravog integrala, baš je unakažena (dobro, nije tak reko, bilo je dost psovki) i to ga je jako frustriralo. I nažalost, ja nisam vidio neki razlog zašt to radit. Pouzdajući se u veliku mudrost 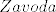 sam to pitanje postavio ovdje uz nadu da će netko (Ilja) odgovorit na njega. Ispričavam se ako sam naporan, to je sve radi imidža matematike kod običnih smrtnika. sam to pitanje postavio ovdje uz nadu da će netko (Ilja) odgovorit na njega. Ispričavam se ako sam naporan, to je sve radi imidža matematike kod običnih smrtnika.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 10:21 ned, 8. 10. 2006 Naslov: Postano: 10:21 ned, 8. 10. 2006 Naslov: |
    |
|
|
I Ilja, sry, znam da si reko da bi vjeko bolje to znao, a i vjerojatno je teško izmislit razumljiv primjer na kojem se vidi primjena toga. Ak budeš znao, dobiš čokoladu.
I Ilja, sry, znam da si reko da bi vjeko bolje to znao, a i vjerojatno je teško izmislit razumljiv primjer na kojem se vidi primjena toga. Ak budeš znao, dobiš čokoladu.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 13:36 ned, 8. 10. 2006 Naslov: Postano: 13:36 ned, 8. 10. 2006 Naslov: |
    |
|
|
U bolesno doba noci (kao npr. sada), poslije sadrzajnog matematickog druzenja :drinking: navratim ponekad na Forum, tako da bi mi sad bilo veselje ako mogu odgovoriti umjesto kolege [b]Ilje[/b].
Mnoga pitanja Fourierove analize su vrlo teska, neke slutnje su dokazane tek 100-tinjak godina nakon sto su postavljene. Zato te ne treba zabrinjavati ako ne mozes sam odgovoriti na sva pitanja (npr. u vezi konvergencije Fourierovih redova), jer ukoliko nisu ocigledna, vjerojatno su prilicno teska. Po tome se recimo Fourierovi redovi razlikuju od Taylorovih (ili Laurentovih) redova potencija.
Osnovna ideja Fourierove analize, kao sto i sam velis, jest prouciti prikaz funkcije pomocu harmonika.
Ukoliko je f:R->C 2pi-periodicna, onda je pokusavamo razviti u Fourierov red, tj. "rastaviti" je na sumu (s odgovarajucim koeficijentima) funkcija oblika e^(ikx), ili (sto je ekvivalentno) sinusa i kosinusa.
Recimo zamisli da imas funkciju f(x)=7cos(2x)+8cos(3x)+9cos(4x) zadanu tako da ti nije odmah jasno od kojih funkcija je slozena, recimo netko ti je posalje kao signal koji tek treba dekomponirati na elementarne "harmonike". Onda izracunas Fourierove koeficijente koji ti kazu da su frekvencije 2, 3, 4 zastupljene redom u omjeru 7, 8, 9. Nakon toga ako treba mozes opet rekonstruirati polaznu funkciju f (signal).
Ukoliko funkcija f nije periodicna, onda je pokusavamo prikazati kao integral pod kojim se opet pojavljuju "harmonici" e^(itx), tj. sinusi i kosinusi.
Razlika je sto sada dozvoljavamo da frekvencije budu bilo kakvi realni brojevi, ne nuzno cijeli. Zato umjesto sume po svim cijelim brojevima pisemo integral po svim realnim brojevima.
Prilicno je tesko dati uvjete na funkciju f uz koje se to moze napraviti, a ti uvjeti ovise i tipu konvergencije kojeg proucavamo (uniforma, po tockama, u nekoj L^p normi...)
FERovci i slicni ljudi od primjene se cesto ne zamaraju pretjerano oko tih uvjeta nego valjda pretpostavljaju da uvijek rade s "dovoljno dobrim" funkcijama, tako da ove uvjete koje si napisao (kao i egzistenciju napisanih integrala) uzmi sa rezervom, a i nemoj se zamarati njima.
U primjeru koji si napisao vrsi se tzv. Fourierova transformacija funkcije f, tj. prikaz funkcije pomocu Fourierovog integrala. To znaci da funkciji f pridruzujemo vrijednosti [latex]A(\lambda)[/latex] i [latex]B(\lambda)[/latex], sto su zapravo funkcije u varijabli [latex]\lambda[/latex]. Matematicari obicno preferiraju jedinstvenu funkciju [latex]\hat{f}(\lambda)= \int_{\mathbb{R}}f(\xi)e^{i\lambda\xi}d\xi[/latex] umjesto [latex]A[/latex] i [latex]B[/latex], ali je nacelno svejedno kako se gleda.
Zamislimo sada da nasa funkcija f predstavlja neki signal, recimo na x-osi je vrijeme, a na y-osi je intenzitet signala f(x) u trenutku x. Sto predstavljaju [latex]A[/latex] i [latex]B[/latex]? Kad pogledas definiciju, moze se zakljuciti da te velicine govore o oscilaciji signala f, a znas da oscilatorno gibanje ima neku svoju frekvenciju ili je sastavljeno od vise fekvencija, ne nuzno konacno njih. (Usporedi s gornjim primjerom za Fourierove redove.) Tako da brojevi [latex]A(\lambda)[/latex] i [latex]B(\lambda)[/latex] govore koliko je frekvencija [latex]\lambda[/latex] zastupljena u signalu f.
Sam Fourierov integral vrsi rekonstrukciju funkcije f iz funkcija [latex]A(\lambda)[/latex] i [latex]B(\lambda)[/latex], tj. zeli se naglasiti da po potrebi mozemo iz [latex]A[/latex] i [latex]B[/latex] opet dobiti polaznu funkciju f. (Ovo je isto malo slampavo jer takav integral konvergira tek uz neke posebne uvjete i u izvjesnom smislu konvergencije, tj. sumabilnosti.) To je razlog sto na kraju pisemo f(x)=ruzni_integral.
Sto se tice matematicke primjene Fourierove analize, prirodno je pokusati funkciju predstaviti na nesto drukciji nacim iz kojeg ce se mozda jasnije vidjeti neka njena svojstva. Recimo ono ruzno cudo pod integralom koji si napisao je (ugrubo) tzv. Fourierova transformacija funkcije f. Ako konvoluiras dvije funkcije (to je jedna posebna binarna operacija na funkcijama), efekt je isti kao da naprosto pomnozis njihove Fourierove transformate (sto je bar teoretski jednostavnije). Ili recimo glatkoca funkcije (to su ona svojstva tipa klase C^1, C^2,...) se moze izraziti pomocu "velicine" njezinog Fourierovog tranformata, i obratno.
Npr. funkcija f koju si napisao nije jako lijepa jer nije neprekidna, pa zato ono cudo pod integralom ne trne jako brzo u beskonacnosti. Obratno, kako je funkcija f dobro lokalizirana, ono pod integralom je klase C^beskonacno. Za precizniju diskusiju bi trebalo uvesti dosta pojmova pa nemoj ni s time pretjerano razbijati glavu.
Evo ti za kraj jos jedan slampavi primjer zasto je Fourierova transformacija korisna. Moze se pokazati da ako deriviras funkciju f(x), njen Fourierov transformat [latex]\hat{f}(\lambda)[/latex] se naprosto pomnozi s [latex]\lambda[/latex].
Zato kad recimo na diferencijalnu jednadzbu
[latex]f''+3f'+2f=g[/latex]
primijenis Fourierovu transformaciju dobit ces naprosto
[latex]\lambda^2 \hat{f}(\lambda)+3\lambda \hat{f}(\lambda)+2\hat{f}(\lambda)=\hat{g}(\lambda)[/latex]
odakle se izluci i izrazi [latex]\hat{f}(\lambda)[/latex] pa se tako (pomocu Fourierovog integrala) moze dobiti rjesenje f polazne diferencijalne jednadzbe.
Sve ovo gore je dosta nejasno ispricano, ali te stvari nisu dovoljne elementarne da bi ih se strogo moglo objasniti na nivou osnova analize. :(
I ako ti se cini da bi te ove stvari mogle zanimati, nemoj ih molim te uciti od FERovaca. :) U vecini matematickih knjiga one su puno ljepse, preglednije i preciznije obradjene, FERovcima je to samo tehnika, ne zamaraju se s detaljima.
P.S.
I hvala ti, [b]alene[/b], sto me se tako lijepo spominjes i drago mi je da si [b]jos uvijek[/b] mlad i ambiciozan. Jedino me malo osupnulo da nisi znao za [i]Dirichletovu funkciju[/i], ali ne moze ti se zamjeriti jer ionako nije R-integrabilna. :wink:
Recimo ja se nisam nocas znao vratit doma pa sam uzeo taxi. :bricks: Hmmm, da.....
U bolesno doba noci (kao npr. sada), poslije sadrzajnog matematickog druzenja  navratim ponekad na Forum, tako da bi mi sad bilo veselje ako mogu odgovoriti umjesto kolege Ilje. navratim ponekad na Forum, tako da bi mi sad bilo veselje ako mogu odgovoriti umjesto kolege Ilje.
Mnoga pitanja Fourierove analize su vrlo teska, neke slutnje su dokazane tek 100-tinjak godina nakon sto su postavljene. Zato te ne treba zabrinjavati ako ne mozes sam odgovoriti na sva pitanja (npr. u vezi konvergencije Fourierovih redova), jer ukoliko nisu ocigledna, vjerojatno su prilicno teska. Po tome se recimo Fourierovi redovi razlikuju od Taylorovih (ili Laurentovih) redova potencija.
Osnovna ideja Fourierove analize, kao sto i sam velis, jest prouciti prikaz funkcije pomocu harmonika.
Ukoliko je f:R→C 2pi-periodicna, onda je pokusavamo razviti u Fourierov red, tj. "rastaviti" je na sumu (s odgovarajucim koeficijentima) funkcija oblika e^(ikx), ili (sto je ekvivalentno) sinusa i kosinusa.
Recimo zamisli da imas funkciju f(x)=7cos(2x)+8cos(3x)+9cos(4x) zadanu tako da ti nije odmah jasno od kojih funkcija je slozena, recimo netko ti je posalje kao signal koji tek treba dekomponirati na elementarne "harmonike". Onda izracunas Fourierove koeficijente koji ti kazu da su frekvencije 2, 3, 4 zastupljene redom u omjeru 7, 8, 9. Nakon toga ako treba mozes opet rekonstruirati polaznu funkciju f (signal).
Ukoliko funkcija f nije periodicna, onda je pokusavamo prikazati kao integral pod kojim se opet pojavljuju "harmonici" e^(itx), tj. sinusi i kosinusi.
Razlika je sto sada dozvoljavamo da frekvencije budu bilo kakvi realni brojevi, ne nuzno cijeli. Zato umjesto sume po svim cijelim brojevima pisemo integral po svim realnim brojevima.
Prilicno je tesko dati uvjete na funkciju f uz koje se to moze napraviti, a ti uvjeti ovise i tipu konvergencije kojeg proucavamo (uniforma, po tockama, u nekoj L^p normi...)
FERovci i slicni ljudi od primjene se cesto ne zamaraju pretjerano oko tih uvjeta nego valjda pretpostavljaju da uvijek rade s "dovoljno dobrim" funkcijama, tako da ove uvjete koje si napisao (kao i egzistenciju napisanih integrala) uzmi sa rezervom, a i nemoj se zamarati njima.
U primjeru koji si napisao vrsi se tzv. Fourierova transformacija funkcije f, tj. prikaz funkcije pomocu Fourierovog integrala. To znaci da funkciji f pridruzujemo vrijednosti 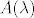 i i 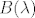 , sto su zapravo funkcije u varijabli , sto su zapravo funkcije u varijabli  . Matematicari obicno preferiraju jedinstvenu funkciju . Matematicari obicno preferiraju jedinstvenu funkciju 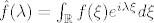 umjesto umjesto  i i  , ali je nacelno svejedno kako se gleda. , ali je nacelno svejedno kako se gleda.
Zamislimo sada da nasa funkcija f predstavlja neki signal, recimo na x-osi je vrijeme, a na y-osi je intenzitet signala f(x) u trenutku x. Sto predstavljaju  i i  ? Kad pogledas definiciju, moze se zakljuciti da te velicine govore o oscilaciji signala f, a znas da oscilatorno gibanje ima neku svoju frekvenciju ili je sastavljeno od vise fekvencija, ne nuzno konacno njih. (Usporedi s gornjim primjerom za Fourierove redove.) Tako da brojevi ? Kad pogledas definiciju, moze se zakljuciti da te velicine govore o oscilaciji signala f, a znas da oscilatorno gibanje ima neku svoju frekvenciju ili je sastavljeno od vise fekvencija, ne nuzno konacno njih. (Usporedi s gornjim primjerom za Fourierove redove.) Tako da brojevi 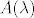 i i 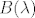 govore koliko je frekvencija govore koliko je frekvencija  zastupljena u signalu f. zastupljena u signalu f.
Sam Fourierov integral vrsi rekonstrukciju funkcije f iz funkcija 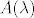 i i 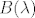 , tj. zeli se naglasiti da po potrebi mozemo iz , tj. zeli se naglasiti da po potrebi mozemo iz  i i  opet dobiti polaznu funkciju f. (Ovo je isto malo slampavo jer takav integral konvergira tek uz neke posebne uvjete i u izvjesnom smislu konvergencije, tj. sumabilnosti.) To je razlog sto na kraju pisemo f(x)=ruzni_integral. opet dobiti polaznu funkciju f. (Ovo je isto malo slampavo jer takav integral konvergira tek uz neke posebne uvjete i u izvjesnom smislu konvergencije, tj. sumabilnosti.) To je razlog sto na kraju pisemo f(x)=ruzni_integral.
Sto se tice matematicke primjene Fourierove analize, prirodno je pokusati funkciju predstaviti na nesto drukciji nacim iz kojeg ce se mozda jasnije vidjeti neka njena svojstva. Recimo ono ruzno cudo pod integralom koji si napisao je (ugrubo) tzv. Fourierova transformacija funkcije f. Ako konvoluiras dvije funkcije (to je jedna posebna binarna operacija na funkcijama), efekt je isti kao da naprosto pomnozis njihove Fourierove transformate (sto je bar teoretski jednostavnije). Ili recimo glatkoca funkcije (to su ona svojstva tipa klase C^1, C^2,...) se moze izraziti pomocu "velicine" njezinog Fourierovog tranformata, i obratno.
Npr. funkcija f koju si napisao nije jako lijepa jer nije neprekidna, pa zato ono cudo pod integralom ne trne jako brzo u beskonacnosti. Obratno, kako je funkcija f dobro lokalizirana, ono pod integralom je klase C^beskonacno. Za precizniju diskusiju bi trebalo uvesti dosta pojmova pa nemoj ni s time pretjerano razbijati glavu.
Evo ti za kraj jos jedan slampavi primjer zasto je Fourierova transformacija korisna. Moze se pokazati da ako deriviras funkciju f(x), njen Fourierov transformat 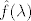 se naprosto pomnozi s se naprosto pomnozi s  . .
Zato kad recimo na diferencijalnu jednadzbu
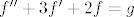
primijenis Fourierovu transformaciju dobit ces naprosto
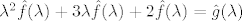
odakle se izluci i izrazi 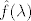 pa se tako (pomocu Fourierovog integrala) moze dobiti rjesenje f polazne diferencijalne jednadzbe. pa se tako (pomocu Fourierovog integrala) moze dobiti rjesenje f polazne diferencijalne jednadzbe.
Sve ovo gore je dosta nejasno ispricano, ali te stvari nisu dovoljne elementarne da bi ih se strogo moglo objasniti na nivou osnova analize. 
I ako ti se cini da bi te ove stvari mogle zanimati, nemoj ih molim te uciti od FERovaca.  U vecini matematickih knjiga one su puno ljepse, preglednije i preciznije obradjene, FERovcima je to samo tehnika, ne zamaraju se s detaljima. U vecini matematickih knjiga one su puno ljepse, preglednije i preciznije obradjene, FERovcima je to samo tehnika, ne zamaraju se s detaljima.
P.S.
I hvala ti, alene, sto me se tako lijepo spominjes i drago mi je da si jos uvijek mlad i ambiciozan. Jedino me malo osupnulo da nisi znao za Dirichletovu funkciju, ali ne moze ti se zamjeriti jer ionako nije R-integrabilna. 
Recimo ja se nisam nocas znao vratit doma pa sam uzeo taxi.  Hmmm, da..... Hmmm, da.....
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 14:08 ned, 8. 10. 2006 Naslov: Postano: 14:08 ned, 8. 10. 2006 Naslov: |
    |
|
|
Super mi je ovo, čak sam većinu stvari skužio. Hvala tebi što si mi napiso tak opširan odgovor.
Da, znam da su ferovci fuj, i da ništ ne valjaju, i da nam na predavanjima govore da se ne družimo s ferovcima, ali, ha bože moj, i oni su ljudi i pokušavaju u barem nekoj mjeri shvatit zašt nešt smiju radit i čem te stvari služe, iako znam da jako malo stvari od tog mogu zapravo skužit, a o dokazivanju da ne pričam, ali svejedno im, unatoč svim njhovim manjkavostima i ograničenostima, ne bismo trebali okrenuti leđa ako pokušavaju to uzaludno shvatit :twisted: .
Da, valjda ću i ja s vremenom ostarit i prestat bit ambiciozan, al dotad moram još puno učit da budem velik i jak ko asistenti Zavoda.
A i bio si super asistent, tak da mi nije problem reć par dobrih riječi o tebi, jedino sam bio razočaran kad sam saznao da je Ilja sa svojima radio Dirichletovu funkciju i da nije R-integrabilna, a kod nas na vježbama o tome nije bilo ni riječi :) .
Trenutno mi je puno veći problem [latex]f\left( x \right) = \sqrt x[/latex], nije mi jasno šta taj znak znači.
Želim ti ugodno :drinking: druženje. :twisted:
Super mi je ovo, čak sam većinu stvari skužio. Hvala tebi što si mi napiso tak opširan odgovor.
Da, znam da su ferovci fuj, i da ništ ne valjaju, i da nam na predavanjima govore da se ne družimo s ferovcima, ali, ha bože moj, i oni su ljudi i pokušavaju u barem nekoj mjeri shvatit zašt nešt smiju radit i čem te stvari služe, iako znam da jako malo stvari od tog mogu zapravo skužit, a o dokazivanju da ne pričam, ali svejedno im, unatoč svim njhovim manjkavostima i ograničenostima, ne bismo trebali okrenuti leđa ako pokušavaju to uzaludno shvatit  . .
Da, valjda ću i ja s vremenom ostarit i prestat bit ambiciozan, al dotad moram još puno učit da budem velik i jak ko asistenti Zavoda.
A i bio si super asistent, tak da mi nije problem reć par dobrih riječi o tebi, jedino sam bio razočaran kad sam saznao da je Ilja sa svojima radio Dirichletovu funkciju i da nije R-integrabilna, a kod nas na vježbama o tome nije bilo ni riječi  . .
Trenutno mi je puno veći problem 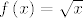 , nije mi jasno šta taj znak znači. , nije mi jasno šta taj znak znači.
Želim ti ugodno  druženje. druženje. 
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 10:16 pon, 9. 10. 2006 Naslov: Postano: 10:16 pon, 9. 10. 2006 Naslov: |
    |
|
|
Alene, dobro da me Vjeko preduhitrio, jer ti ja ja to sigurno ne bi tako lijepo objasnio. A i nemam što pametno za dodati, osim da je Fourierova transformacija dosta bitna u teoriji valića (valići su neke funkcije s kojima generiraš ortonormiranu bazu za prostor L^2 koristeći dilatacije i ekspanzije). Ono što je tu zanimljivo je da nemaš karakterizaciju kada je neka funkcija valić izraženu pomoću same funkcije, ali imamo karakterizaciju izraženu pomoću njene Fourierove transformacije. Znači, bitan je raspon i intenzitet frekvencija koje dana funkcija "emitira".
I nemoj se bedirati što Dirichletova funkcija nije Riemann-integrabilna, jer Lebesgue-integrabilna je, a Lebesgueov integeral je više kul (ispalo po zadnjoj anketi). :wink:
Alene, dobro da me Vjeko preduhitrio, jer ti ja ja to sigurno ne bi tako lijepo objasnio. A i nemam što pametno za dodati, osim da je Fourierova transformacija dosta bitna u teoriji valića (valići su neke funkcije s kojima generiraš ortonormiranu bazu za prostor L^2 koristeći dilatacije i ekspanzije). Ono što je tu zanimljivo je da nemaš karakterizaciju kada je neka funkcija valić izraženu pomoću same funkcije, ali imamo karakterizaciju izraženu pomoću njene Fourierove transformacije. Znači, bitan je raspon i intenzitet frekvencija koje dana funkcija "emitira".
I nemoj se bedirati što Dirichletova funkcija nije Riemann-integrabilna, jer Lebesgue-integrabilna je, a Lebesgueov integeral je više kul (ispalo po zadnjoj anketi). 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 10:35 pon, 9. 10. 2006 Naslov: Postano: 10:35 pon, 9. 10. 2006 Naslov: |
    |
|
|
Da, stvarno je dobro objasnio, al nisi ni ti za bacit. Zbog vas 2 i još nekih ljudi sam ponosan što sam na ovom faksu.
Usput, mislim da sam skužio ono s razlomcima. Na primjer
[latex]\begin{array}{l}
y: = \frac{2}{3} + \frac{{11}}{5} \Rightarrow 3y = 3 \cdot \left( {\frac{2}{3} + \frac{{11}}{5}} \right) = 3 \cdot \frac{2}{3} + 3 \cdot \frac{{11}}{5} = \\
= 2 + 3 \cdot \frac{{11}}{5} \Rightarrow 5 \cdot \left( {3y} \right) = 5 \cdot 2 + 5 \cdot \left( {3 \cdot \frac{{11}}{5}} \right) = \\
= 10 + 3 \cdot \left( {5 \cdot \frac{{11}}{5}} \right) = 10 + 3 \cdot 11 = 10 + 33 = 43 \Rightarrow \\
\Rightarrow 15y = 43 \\
\end{array}[/latex]
Jedino sad ne znam šta da radim da dobijem [latex]y[/latex], al osjećam dasam dost blizu rješenja.
Da, stvarno je dobro objasnio, al nisi ni ti za bacit. Zbog vas 2 i još nekih ljudi sam ponosan što sam na ovom faksu.
Usput, mislim da sam skužio ono s razlomcima. Na primjer
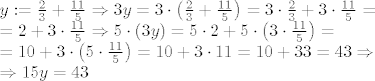
Jedino sad ne znam šta da radim da dobijem  , al osjećam dasam dost blizu rješenja. , al osjećam dasam dost blizu rješenja.
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 11:34 pon, 9. 10. 2006 Naslov: Postano: 11:34 pon, 9. 10. 2006 Naslov: |
    |
|
|
E da, skoro zaboravih. Fourierova transformacija je esencijalni aparat u kvantnoj mehanici. Npr. stanje čestice je opisano valnom funkcijom [latex]\psi : \mathbb{R}^3 \times \mathbb{R} \rightarrow \mathbb{C}[/latex], gdje je [latex]|\psi(\cdot, t)|^2[/latex] funkcija gustoće vjerojatnosti položaja čestice u trenutku [latex]t[/latex], tj. vjerojatnost da će se čestica u trenutku [latex]t[/latex] nalaziti unutar područja [latex]\Omega \subseteq \mathbb{R}^3[/latex] je [latex]\int_{\Omega}|\psi(x,t)|^2 dx[/latex]. Također, ta valna funkcija [latex]\psi[/latex] zadovoljava neku parcijalnu diferencijalnu jednadžbu (Schrodingerovu jednadžbu), no to sad nije bitno.
Onaj poznati Heissenbergov princip neodređenosti kaže da je nemoguće [b]istovremeno[/b] predvidjeti položaj i moment čestice sa po volji odabranom točnošću. U matematičkom obliku, to ima veze sa činjenicom da nije moguće istovremeno lokalizirati funkciju [latex]\psi[/latex] (koja ima veze s položajem čestice) i njenu Fourierovu transformaciju [latex]\widehat{\psi}[/latex] (koja ima veze s momentom čestice).
Znači, grubo rečeno, ne možeš istovremeno zahtijevati da funkcija [latex]\psi[/latex] i njena Fourierova transformacija iščezavaju van skupova po volji male mjere. Eto. :D
E da, skoro zaboravih. Fourierova transformacija je esencijalni aparat u kvantnoj mehanici. Npr. stanje čestice je opisano valnom funkcijom 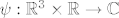 , gdje je , gdje je 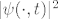 funkcija gustoće vjerojatnosti položaja čestice u trenutku funkcija gustoće vjerojatnosti položaja čestice u trenutku  , tj. vjerojatnost da će se čestica u trenutku , tj. vjerojatnost da će se čestica u trenutku  nalaziti unutar područja nalaziti unutar područja  je je 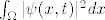 . Također, ta valna funkcija . Također, ta valna funkcija 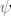 zadovoljava neku parcijalnu diferencijalnu jednadžbu (Schrodingerovu jednadžbu), no to sad nije bitno. zadovoljava neku parcijalnu diferencijalnu jednadžbu (Schrodingerovu jednadžbu), no to sad nije bitno.
Onaj poznati Heissenbergov princip neodređenosti kaže da je nemoguće istovremeno predvidjeti položaj i moment čestice sa po volji odabranom točnošću. U matematičkom obliku, to ima veze sa činjenicom da nije moguće istovremeno lokalizirati funkciju 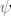 (koja ima veze s položajem čestice) i njenu Fourierovu transformaciju (koja ima veze s položajem čestice) i njenu Fourierovu transformaciju 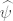 (koja ima veze s momentom čestice). (koja ima veze s momentom čestice).
Znači, grubo rečeno, ne možeš istovremeno zahtijevati da funkcija 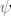 i njena Fourierova transformacija iščezavaju van skupova po volji male mjere. Eto. i njena Fourierova transformacija iščezavaju van skupova po volji male mjere. Eto. 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 21:58 pon, 9. 10. 2006 Naslov: Postano: 21:58 pon, 9. 10. 2006 Naslov: |
    |
|
|
[quote="alen"]Siguran sam da će FERovac bit oduševljen primjenom u kvantnoj mehanici :twisted: . Znam da ću ja bit.[/quote]
Bolje ti ferovcu nađi neku curu (tranzistor). [size=7]Jel znaš možda za neki tečaj da malo poradim na svom humoru?
[/size]
[quote="alen"]
Jel ćeš ti držat vježbe iz numeričke u drugom semestru? (pliz, reci da) [/quote]
Neću. :D Al možda ti zeix bude demos, on ti je macan i pol. :squirrel: Ovo je vjeverica. [size=7]Neki stvarno dobar tečaj?[/size]
[quote="alen"]
Sad sam čuo neke glasine da nećeš, al jel bi mogo bar iz bilo čega, to ti je sam 2 sata na tjedan?[/quote]
Baš lijepo od tebe, ali mislim da sam već dovoljo osakatio vašu generaciju (posebno moju prošlogodišnju grupu G-K kojoj ovom prilikom šaljem pusu). Ovu patetiku završit ću sa izrekom mudrog (ali pokojnog) dr. Exodusa :croatia: koja kaže:
[img]http://www.virovitica-online.com/kolumne/images/000342s.jpg[/img]
| alen (napisa): | Siguran sam da će FERovac bit oduševljen primjenom u kvantnoj mehanici  . Znam da ću ja bit. . Znam da ću ja bit. |
Bolje ti ferovcu nađi neku curu (tranzistor). Jel znaš možda za neki tečaj da malo poradim na svom humoru?
| alen (napisa): |
Jel ćeš ti držat vježbe iz numeričke u drugom semestru? (pliz, reci da) |
Neću.  Al možda ti zeix bude demos, on ti je macan i pol. Al možda ti zeix bude demos, on ti je macan i pol.  Ovo je vjeverica. Neki stvarno dobar tečaj? Ovo je vjeverica. Neki stvarno dobar tečaj?
| alen (napisa): |
Sad sam čuo neke glasine da nećeš, al jel bi mogo bar iz bilo čega, to ti je sam 2 sata na tjedan? |
Baš lijepo od tebe, ali mislim da sam već dovoljo osakatio vašu generaciju (posebno moju prošlogodišnju grupu G-K kojoj ovom prilikom šaljem pusu). Ovu patetiku završit ću sa izrekom mudrog (ali pokojnog) dr. Exodusa  koja kaže: koja kaže:

|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 9:00 uto, 10. 10. 2006 Naslov: Postano: 9:00 uto, 10. 10. 2006 Naslov: |
    |
|
|
[quote="Ilja"]Bolje ti ferovcu nađi neku curu (tranzistor). [size=7]Jel znaš možda za neki tečaj da malo poradim na svom humoru?
[/size][/quote]
Ima curu. Ja mu našo već 2 (za tranzistor nisam siguran). [size=7]Ne znam, al među nama, humor ti je dobar, nemoj nikom reć[/size]
[quote="Ilja"]
Neću. :D Al možda ti zeix bude demos, on ti je macan i pol. [/quote]
Wheeee, to će bit skoro isto ko da mi držiš vježbe (s obzirom na to da skoro nikad ne idem na demonstrature).
[quote="Ilja"]
:squirrel: Ovo je vjeverica. [size=7]Neki stvarno dobar tečaj?[/size]
[/quote]
Zaprepašten sam :shock: . [size=7]Al stvarno ti je dobar humor[/size]
[quote="Ilja"]
Baš lijepo od tebe, ali mislim da sam već dovoljo osakatio vašu generaciju (posebno moju prošlogodišnju grupu G-K kojoj ovom prilikom šaljem pusu). Ovu patetiku završit ću sa izrekom mudrog (ali pokojnog) dr. Exodusa :croatia: koja kaže:
[img]http://www.virovitica-online.com/kolumne/images/000342s.jpg[/img]
[/quote]
[size=7]Vidim da je slika s virovitica-online, a ja sam iz Virovitice, tak da me zanima jel to tolko suptilni humor da ga ni ja ne kužim, ili se tu radi o nečem drugom, ili je to samo slučajnost? [/size]
Vidjet ćeš ti nasilje, organizirat ću kolege s 2. godine i mučit ćemo te dok ne popustiš i pristaneš nam bit asistent. :twisted:
| Ilja (napisa): | Bolje ti ferovcu nađi neku curu (tranzistor). Jel znaš možda za neki tečaj da malo poradim na svom humoru?
|
Ima curu. Ja mu našo već 2 (za tranzistor nisam siguran). Ne znam, al među nama, humor ti je dobar, nemoj nikom reć
| Ilja (napisa): |
Neću.  Al možda ti zeix bude demos, on ti je macan i pol. Al možda ti zeix bude demos, on ti je macan i pol. |
Wheeee, to će bit skoro isto ko da mi držiš vježbe (s obzirom na to da skoro nikad ne idem na demonstrature).
| Ilja (napisa): |
 Ovo je vjeverica. Neki stvarno dobar tečaj? Ovo je vjeverica. Neki stvarno dobar tečaj?
|
Zaprepašten sam  . Al stvarno ti je dobar humor . Al stvarno ti je dobar humor
| Ilja (napisa): |
Baš lijepo od tebe, ali mislim da sam već dovoljo osakatio vašu generaciju (posebno moju prošlogodišnju grupu G-K kojoj ovom prilikom šaljem pusu). Ovu patetiku završit ću sa izrekom mudrog (ali pokojnog) dr. Exodusa  koja kaže: koja kaže:

|
Vidim da je slika s virovitica-online, a ja sam iz Virovitice, tak da me zanima jel to tolko suptilni humor da ga ni ja ne kužim, ili se tu radi o nečem drugom, ili je to samo slučajnost?
Vidjet ćeš ti nasilje, organizirat ću kolege s 2. godine i mučit ćemo te dok ne popustiš i pristaneš nam bit asistent. 
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 9:33 uto, 10. 10. 2006 Naslov: Postano: 9:33 uto, 10. 10. 2006 Naslov: |
    |
|
|
[quote="Ilja"]Jel znaš možda za neki tečaj da malo poradim na svom humoru?[/quote]
[quote="Ilja"]Neki stvarno dobar tečaj?[/quote]
Mi ovdje u Los Endželesu imamo jedan jako dobar nedjeljni tečaj, zove se [i]Big Momma Does Math[/i]. :valjalo:
Polazim ga redovito i mogu reci da sam vec dosta uznapredovao sto se tice smisla za humor. Sad tek vidim kakvo zlo smo Ilja i ja cinili nekoc nedavno tu na forumu, a sve u neznanju.
Recimo zadnji put smo naucili:
[latex]\mathrm{coset}=\sqrt{1-\mathrm{set}^2}[/latex]
a za zadacu smo dobili
[latex]\mathrm{CheGuevara}=\sqrt{\hspace{7mm}}[/latex]
Sto se tice te zadace, molio bih da mi netko malo pomogne. Kako sad to Čegevara moze biti jednak korijenu, sto je tu kvaka, ne kužim bas. Hvala lijepa!
Sad se vise uopce ne mogu ni nasmijati losim vicevima, kolko sam vec napredan. Evo primjera jednog takvog loseg vica koji bi me nekoc sigurno nasmijao. Jedino sto ga ne smijem napisati ovdje zato sto je malo nepristojan, ali zato evo [url=http://funatic.redir.dizzy.hr/vicevi.asp?fs=ribica+guzica+ptica&tip=1&submit=Tra%9Ei][b]LINK[/b][/url]
:kipslobode:
| Ilja (napisa): | | Jel znaš možda za neki tečaj da malo poradim na svom humoru? |
| Ilja (napisa): | | Neki stvarno dobar tečaj? |
Mi ovdje u Los Endželesu imamo jedan jako dobar nedjeljni tečaj, zove se Big Momma Does Math. 
Polazim ga redovito i mogu reci da sam vec dosta uznapredovao sto se tice smisla za humor. Sad tek vidim kakvo zlo smo Ilja i ja cinili nekoc nedavno tu na forumu, a sve u neznanju.
Recimo zadnji put smo naucili:
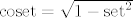
a za zadacu smo dobili
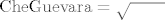
Sto se tice te zadace, molio bih da mi netko malo pomogne. Kako sad to Čegevara moze biti jednak korijenu, sto je tu kvaka, ne kužim bas. Hvala lijepa!
Sad se vise uopce ne mogu ni nasmijati losim vicevima, kolko sam vec napredan. Evo primjera jednog takvog loseg vica koji bi me nekoc sigurno nasmijao. Jedino sto ga ne smijem napisati ovdje zato sto je malo nepristojan, ali zato evo LINK

|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
|






