kad se radio lin. reg. model profesor Huzak je, prije nego
sto se obradi "Normalno distribuirane greske", podijelio
jedan A4 papir s par zadataka za domaci. Jedan od njih je:
---------
Neka su P i Q ortogonalni projektori reda n takvi da je I=P+Q.
Tada postoji ortogonalna matrica U takva da je
[latex]
U^{*}PU=
\left( \begin{array}{cc}
I_{p} & 0_{pq} \\
0_{qp} & 0_{q}
\end{array} \right)
\hspace{1cm} U^{*}QU=
\left( \begin{array}{cc}
0_{p} & 0_{pq} \\
0_{qp} & I_{q}
\end{array} \right)
[/latex]
gdje su Ip i Iq jedinicne matrice reda p=r(P), odnosno q=r(Q).
---------
E sad, mene zanima jel netko pronasao odakle je to izvuceno,
te kako iz toga slijedi:
---------
Neka je X ~ N(0,1) standardni n-dim normalni slucajni vektor,
te neka su P i Q ortogonalni projektori t.d. I=P+Q, te ranga p i q,
redom. Tada slucajni vektor PX ima normalnu razdiobu s ocekivanjem 0
i kovarijacijskom matricom
[latex]
\left( \begin{array}{cc}
I_{p} & 0_{pq} \\
0_{qp} & 0_{q}
\end{array} \right)
[/latex]
---------
kad se radio lin. reg. model profesor Huzak je, prije nego
sto se obradi "Normalno distribuirane greske", podijelio
jedan A4 papir s par zadataka za domaci. Jedan od njih je:
---------
Neka su P i Q ortogonalni projektori reda n takvi da je I=P+Q.
Tada postoji ortogonalna matrica U takva da je

gdje su Ip i Iq jedinicne matrice reda p=r(P), odnosno q=r(Q).
---------
E sad, mene zanima jel netko pronasao odakle je to izvuceno,
te kako iz toga slijedi:
---------
Neka je X ~ N(0,1) standardni n-dim normalni slucajni vektor,
te neka su P i Q ortogonalni projektori t.d. I=P+Q, te ranga p i q,
redom. Tada slucajni vektor PX ima normalnu razdiobu s ocekivanjem 0
i kovarijacijskom matricom
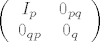
---------
_________________
The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne?




