| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
lyra
Forumaš(ica)

Pridružen/a: 17. 07. 2006. (21:23:44)
Postovi: (63)16
Spol: 
|
 Postano: 15:19 sub, 2. 6. 2007 Naslov: Postano: 15:19 sub, 2. 6. 2007 Naslov: |
    |
|
|
2.) podijeliš brojnik i nazivnik s 3^(2x), pa gore dobiješ (2/3)^x, a dole 1-(2/3)^(2x), pa uvedeš supstituciju t=(2/3)^x, a dalje je lako.
a 3., ako je iz onih zadataka s weba, možda je problem u tome što si krivo prepisao brojnik. :lol:
:wink:
2.) podijeliš brojnik i nazivnik s 3^(2x), pa gore dobiješ (2/3)^x, a dole 1-(2/3)^(2x), pa uvedeš supstituciju t=(2/3)^x, a dalje je lako.
a 3., ako je iz onih zadataka s weba, možda je problem u tome što si krivo prepisao brojnik. 

|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 15:21 sub, 2. 6. 2007 Naslov: Postano: 15:21 sub, 2. 6. 2007 Naslov: |
    |
|
|
Prvi je lagani [latex]\int \frac{x^2}{(1+x^2)^2}dx=\int\frac{1}{1+x^2} dx - \int \frac{1}{(1+x^2)^2}dx [/latex] , mislim da je ovaj drugi tablicni integral , ali ako nije rastavi na par. razlomke i onda ce biti sigurno tablicni (mislim [latex]arctan [/latex] ili nesta slicno .
Za drugi, bas nisam siguran da ce funkcionirati no baci [latex]6^x[/latex] u nazivnik i probaj to srediti ( ja sam malo krenuo sa rjesavanjem no ne izgleda obecavajuce).
Za treci se malo strpi (valjda ce mi nesta pasti na pamet 8) )
Edit: odlicno, kolega/kolegica ti je dala ideju, za drugi zadatak!
Prvi je lagani 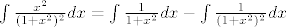 , mislim da je ovaj drugi tablicni integral , ali ako nije rastavi na par. razlomke i onda ce biti sigurno tablicni (mislim , mislim da je ovaj drugi tablicni integral , ali ako nije rastavi na par. razlomke i onda ce biti sigurno tablicni (mislim 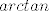 ili nesta slicno . ili nesta slicno .
Za drugi, bas nisam siguran da ce funkcionirati no baci 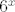 u nazivnik i probaj to srediti ( ja sam malo krenuo sa rjesavanjem no ne izgleda obecavajuce). u nazivnik i probaj to srediti ( ja sam malo krenuo sa rjesavanjem no ne izgleda obecavajuce).
Za treci se malo strpi (valjda ce mi nesta pasti na pamet  ) )
Edit: odlicno, kolega/kolegica ti je dala ideju, za drugi zadatak!
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
 Postano: 16:56 sub, 2. 6. 2007 Naslov: Postano: 16:56 sub, 2. 6. 2007 Naslov: |
    |
|
|
[quote="Mr.Doe"]Prvi je lagani [latex]\int \frac{x^2}{(1+x^2)^2}dx=\int\frac{1}{1+x^2} dx - \int \frac{1}{(1+x^2)^2}dx [/latex] , mislim da je ovaj drugi tablicni integral , ali ako nije rastavi na par. razlomke i onda ce biti sigurno tablicni (mislim [latex]arctan [/latex] ili nesta slicno .
[/quote]
Kod prvog mi je problem baš taj [latex]\int \frac{1}{(1+x^2)^2}dx[/latex] ovo drugo znam da je lagano.
Dakle rastavljam na parcijalne razlomke:
[latex] \frac{1}{(1+x^2)^2}=\frac{Ax+B}{1+x^2} + \frac{Cx+D}{(1+x^2)^2} [/latex]. Problem je u tome šta dobijem A=B=C=0 i D=1, znači dobijem isto ono šta sam pokušao rastaviti. Dali radim nešto krivo ili postoji neki drugi način?
EDIT: Pronašao sam, ovaj se rješava rekurzivno, i dođe [latex] \frac{1}{2}arctgx + \frac{1}{2}\frac{x}{x^2+1} + C[/latex]
| Mr.Doe (napisa): | Prvi je lagani 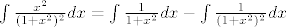 , mislim da je ovaj drugi tablicni integral , ali ako nije rastavi na par. razlomke i onda ce biti sigurno tablicni (mislim , mislim da je ovaj drugi tablicni integral , ali ako nije rastavi na par. razlomke i onda ce biti sigurno tablicni (mislim 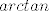 ili nesta slicno . ili nesta slicno .
|
Kod prvog mi je problem baš taj 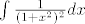 ovo drugo znam da je lagano. ovo drugo znam da je lagano.
Dakle rastavljam na parcijalne razlomke:
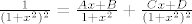 . Problem je u tome šta dobijem A=B=C=0 i D=1, znači dobijem isto ono šta sam pokušao rastaviti. Dali radim nešto krivo ili postoji neki drugi način? . Problem je u tome šta dobijem A=B=C=0 i D=1, znači dobijem isto ono šta sam pokušao rastaviti. Dali radim nešto krivo ili postoji neki drugi način?
EDIT: Pronašao sam, ovaj se rješava rekurzivno, i dođe 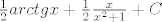
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:17 sub, 2. 6. 2007 Naslov: Postano: 18:17 sub, 2. 6. 2007 Naslov: |
    |
|
|
Bravo...svaka čast, nikad se tog ne bi sjetio...
Bravo...svaka čast, nikad se tog ne bi sjetio...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 20:12 sub, 2. 6. 2007 Naslov: Postano: 20:12 sub, 2. 6. 2007 Naslov: |
    |
|
|
Super cool nacin , no ja sam dobio malo drugacije. Evo mojeg rjesenja;
dakle krenem kako sam rekao i promatram drugi integral ( prvi je jednak [latex]\arctan x[/latex]). Gledamo;
[latex]\frac{1}{(1+x^2)^2}=\frac{1}{1+x^2}\frac{1}{1+x^2}=(\sum_{n=0}
^{\infty} (-1)^n x^{2n} )^2=\sum_{n=0}^{\infty}(-1)^n (n+1)x^{2n}[/latex] . Sada to fino integriramo (koristio sam C- pravilo za produkt redova , dobijemo
[latex]\int \frac{1}{(1+x^2)^2}dx=\sum_{n=0}^{\infty}(-1)^n (\frac{n+1}{2n+1})x^{2n+1}=\{n+1=n+\frac{1}{2}+\frac{1}{2}\}=[/latex]
[latex]
\frac{1}{2} x \sum_{n=0}^{\infty}(-1)^n x^{2n}+
\frac{1}{2}\sum_{n=0}^{\infty}(-1)^n \frac{1}{2n+1}x^{2n+1}[/latex]
Prvi je geometrijski red , a drugi je red od [latex]\arctan [/latex].
Dakle,kad sve to fino zbrojim dobijem
[latex]\frac{x}{2(1+x^2)}+\frac{3}{2}\arctan x[/latex] . Gdje sam pogrjesio :? .
Ipak ja bih jos na kraju dodao jednu veliko konstantu,buduci da ovo moze sve tako lagano divergirati :D .
(znam da dosta toga nisam objasnio, no mislim da za vas ne bi trebalo biti problema ) 8)
Super cool nacin , no ja sam dobio malo drugacije. Evo mojeg rjesenja;
dakle krenem kako sam rekao i promatram drugi integral ( prvi je jednak 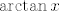 ). Gledamo; ). Gledamo;
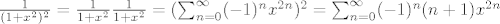 . Sada to fino integriramo (koristio sam C- pravilo za produkt redova , dobijemo . Sada to fino integriramo (koristio sam C- pravilo za produkt redova , dobijemo
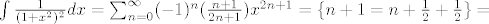
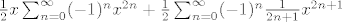
Prvi je geometrijski red , a drugi je red od 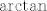 . .
Dakle,kad sve to fino zbrojim dobijem
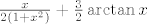 . Gdje sam pogrjesio . Gdje sam pogrjesio  . .
Ipak ja bih jos na kraju dodao jednu veliko konstantu,buduci da ovo moze sve tako lagano divergirati  . .
(znam da dosta toga nisam objasnio, no mislim da za vas ne bi trebalo biti problema ) 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:31 pon, 4. 6. 2007 Naslov: Postano: 20:31 pon, 4. 6. 2007 Naslov: |
    |
|
|
Ako pitanje još uvijek stoji, a nitko ga nije riješio, imam ja rješenje onog integrala pod 3. (tj 19. sa weba).
Ide se parcijalnom integracijom i uzmeš za u ovaj ln ,a za dv x/korijen dx. Sad je v=korijen. Dalje je lako.
Ako pitanje još uvijek stoji, a nitko ga nije riješio, imam ja rješenje onog integrala pod 3. (tj 19. sa weba).
Ide se parcijalnom integracijom i uzmeš za u ovaj ln ,a za dv x/korijen dx. Sad je v=korijen. Dalje je lako.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:26 pet, 8. 6. 2007 Naslov: Postano: 14:26 pet, 8. 6. 2007 Naslov: |
    |
|
|
Sumnjiv mi je 30. zad s weba...meni ispada 0... raspisao sam ono oboje ispod korijena, kosinusi se ubili, korijen iz 2 otišo van i ostao integral od sinusa. Sad dobijem -sqrt(2) * (cos 100pi-cos0) a to je nula. Gdje griješim??
Btw još uvijek čekam 20.zad... pa nije valjda da nitko ne zna...
Sumnjiv mi je 30. zad s weba...meni ispada 0... raspisao sam ono oboje ispod korijena, kosinusi se ubili, korijen iz 2 otišo van i ostao integral od sinusa. Sad dobijem -sqrt(2) * (cos 100pi-cos0) a to je nula. Gdje griješim??
Btw još uvijek čekam 20.zad... pa nije valjda da nitko ne zna...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:51 pet, 8. 6. 2007 Naslov: Postano: 16:51 pet, 8. 6. 2007 Naslov: |
    |
|
|
Hvala, pomoglo je...ja se mučio s onim 1-x^2 a to ustvari sinus na kvadrat...
Daj još molim te napiši kak se vrati ctg(arccosx) u nešt normalno...i sin(arccosx)... ti arcusi su me oduvijek zbunjivali...ne znam zašto...baš ih ne volim...
Hvala, pomoglo je...ja se mučio s onim 1-x^2 a to ustvari sinus na kvadrat...
Daj još molim te napiši kak se vrati ctg(arccosx) u nešt normalno...i sin(arccosx)... ti arcusi su me oduvijek zbunjivali...ne znam zašto...baš ih ne volim...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|





















