| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 0:24 pon, 25. 8. 2008 Naslov: Nekoliko teorijskih pitanja Postano: 0:24 pon, 25. 8. 2008 Naslov: Nekoliko teorijskih pitanja |
    |
|
|
[url=http://web.math.hr/~guljas/skripte/MATANALuR.pdf]Link na skriptu[/url]
1) 143. stranica (ne ona na kojoj piše 143, nego 143. u dokumentu) , dokaz da neprekidna funkcija ima primitivnu, prvi red na stranici koji počinje s "F(x) - F(c)"... Odakle posljednja jednakost u redu?
Također, u tom redu imamo F(x) - F(c) = nešto, a u idućem redu se lijeva strana te jednakosti dijeli sa (x-c) a desna ostane jednaka. Zašto? :?
2) Taylorovi redovi. :shock: Moram li učiti razvoj (i konvergenciju) svake funkcije posebno, postoji li neka šablona, ili se od mene očekuje da ne učim ništa napamet nego iz svih onih teorema sam zaključujem? Recimo, za e na iks sve shvaćam ali već za ln(1+x) mi nije jasno što je tu uopće razvoj, što je dokaz konvergencije i što se dobije odakle i zašto.
Hvala. :D
Link na skriptu
1) 143. stranica (ne ona na kojoj piše 143, nego 143. u dokumentu) , dokaz da neprekidna funkcija ima primitivnu, prvi red na stranici koji počinje s "F(x) - F(c)"... Odakle posljednja jednakost u redu?
Također, u tom redu imamo F(x) - F(c) = nešto, a u idućem redu se lijeva strana te jednakosti dijeli sa (x-c) a desna ostane jednaka. Zašto? 
2) Taylorovi redovi.  Moram li učiti razvoj (i konvergenciju) svake funkcije posebno, postoji li neka šablona, ili se od mene očekuje da ne učim ništa napamet nego iz svih onih teorema sam zaključujem? Recimo, za e na iks sve shvaćam ali već za ln(1+x) mi nije jasno što je tu uopće razvoj, što je dokaz konvergencije i što se dobije odakle i zašto. Moram li učiti razvoj (i konvergenciju) svake funkcije posebno, postoji li neka šablona, ili se od mene očekuje da ne učim ništa napamet nego iz svih onih teorema sam zaključujem? Recimo, za e na iks sve shvaćam ali već za ln(1+x) mi nije jasno što je tu uopće razvoj, što je dokaz konvergencije i što se dobije odakle i zašto.
Hvala. 
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
 Postano: 0:50 pon, 25. 8. 2008 Naslov: Re: Nekoliko teorijskih pitanja Postano: 0:50 pon, 25. 8. 2008 Naslov: Re: Nekoliko teorijskih pitanja |
    |
|
|
[quote="Atomised"]1) 143. stranica (ne ona na kojoj piše 143, nego 143. u dokumentu) , dokaz da neprekidna funkcija ima primitivnu, prvi red na stranici koji počinje s "F(x) - F(c)"... Odakle posljednja jednakost u redu?
Također, u tom redu imamo F(x) - F(c) = nešto, a u idućem redu se lijeva strana te jednakosti dijeli sa (x-c) a desna ostane jednaka. Zašto? :? [/quote]
fali u posljednoj jednakosti još puta (x-c)... pa se onda može podijelit s tim i dobit ono sljedeće :) a kako se dobije ta posljednja jednakost... dakle, po tm. 5.7. imaš da postoji točka između c i x, recimo t, takva da je taj integral jednak f(t)*(x-c)... i sad tu točku t zapišeš u obliku c + θx(x − c)... gdje je θx između 0 i 1... znači, u rubnim slučajevima ti je t=c ( za θx=0) i t=x ( za θx=1), a u svim ostalima je negdje između c i x, pa je zato ok :)
nadam se da je jasnije :D
| Atomised (napisa): | 1) 143. stranica (ne ona na kojoj piše 143, nego 143. u dokumentu) , dokaz da neprekidna funkcija ima primitivnu, prvi red na stranici koji počinje s "F(x) - F(c)"... Odakle posljednja jednakost u redu?
Također, u tom redu imamo F(x) - F(c) = nešto, a u idućem redu se lijeva strana te jednakosti dijeli sa (x-c) a desna ostane jednaka. Zašto?  |
fali u posljednoj jednakosti još puta (x-c)... pa se onda može podijelit s tim i dobit ono sljedeće  a kako se dobije ta posljednja jednakost... dakle, po tm. 5.7. imaš da postoji točka između c i x, recimo t, takva da je taj integral jednak f(t)*(x-c)... i sad tu točku t zapišeš u obliku c + θx(x − c)... gdje je θx između 0 i 1... znači, u rubnim slučajevima ti je t=c ( za θx=0) i t=x ( za θx=1), a u svim ostalima je negdje između c i x, pa je zato ok a kako se dobije ta posljednja jednakost... dakle, po tm. 5.7. imaš da postoji točka između c i x, recimo t, takva da je taj integral jednak f(t)*(x-c)... i sad tu točku t zapišeš u obliku c + θx(x − c)... gdje je θx između 0 i 1... znači, u rubnim slučajevima ti je t=c ( za θx=0) i t=x ( za θx=1), a u svim ostalima je negdje između c i x, pa je zato ok 
nadam se da je jasnije 
_________________ kalendar 
  |
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 0:56 pon, 25. 8. 2008 Naslov: Re: Nekoliko teorijskih pitanja Postano: 0:56 pon, 25. 8. 2008 Naslov: Re: Nekoliko teorijskih pitanja |
    |
|
|
[quote="arya"]
fali u posljednoj jednakosti još puta (x-c)... pa se onda može podijelit s tim i dobit ono sljedeće :) a kako se dobije ta posljednja jednakost... dakle, po tm. 5.7. imaš da postoji točka između c i x, recimo t, takva da je taj integral jednak f(t)*(x-c)... i sad tu točku t zapišeš u obliku c + θx(x − c)... gdje je θx između 0 i 1... znači, u rubnim slučajevima ti je t=c ( za θx=0) i t=x ( za θx=1), a u svim ostalima je negdje između c i x, pa je zato ok :)
nadam se da je jasnije :D[/quote]
Ne znam bih li sada trebao zaključiti da nisam glup jer nije moja greška, ili da sam glup jer nisam uvidio tu (dosta očitu) grešku. :D
U svakom slučaju, sad mi je sve jasno, hvala. :D
| arya (napisa): |
fali u posljednoj jednakosti još puta (x-c)... pa se onda može podijelit s tim i dobit ono sljedeće  a kako se dobije ta posljednja jednakost... dakle, po tm. 5.7. imaš da postoji točka između c i x, recimo t, takva da je taj integral jednak f(t)*(x-c)... i sad tu točku t zapišeš u obliku c + θx(x − c)... gdje je θx između 0 i 1... znači, u rubnim slučajevima ti je t=c ( za θx=0) i t=x ( za θx=1), a u svim ostalima je negdje između c i x, pa je zato ok a kako se dobije ta posljednja jednakost... dakle, po tm. 5.7. imaš da postoji točka između c i x, recimo t, takva da je taj integral jednak f(t)*(x-c)... i sad tu točku t zapišeš u obliku c + θx(x − c)... gdje je θx između 0 i 1... znači, u rubnim slučajevima ti je t=c ( za θx=0) i t=x ( za θx=1), a u svim ostalima je negdje između c i x, pa je zato ok 
nadam se da je jasnije  |
Ne znam bih li sada trebao zaključiti da nisam glup jer nije moja greška, ili da sam glup jer nisam uvidio tu (dosta očitu) grešku. 
U svakom slučaju, sad mi je sve jasno, hvala. 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 10:46 pon, 25. 8. 2008 Naslov: Re: Nekoliko teorijskih pitanja Postano: 10:46 pon, 25. 8. 2008 Naslov: Re: Nekoliko teorijskih pitanja |
    |
|
|
[quote="Atomised"]
2) Taylorovi redovi. :shock: Moram li učiti razvoj (i konvergenciju) svake funkcije posebno, postoji li neka šablona, ili se od mene očekuje da ne učim ništa napamet nego iz svih onih teorema sam zaključujem? Recimo, za e na iks sve shvaćam ali već za ln(1+x) mi nije jasno što je tu uopće razvoj, što je dokaz konvergencije i što se dobije odakle i zašto.
Hvala. :D[/quote]
Najprije da ispravim aryu, θ je iz [0,1], a ne θx :D
A redovi su super :D :D :D
Imaš iz onih tm da se redovi dobro ponašaju na deriviranje, integriranje, zbrajanje i sl. pa sve dobivaš iz toga. Za ln(1+x) kreneš od geom reda.
Dakle znamo da je
[latex]\sum{x^n} = \frac{1}{1-x}[/latex] za x iz <-1,1>
sad uzmemo za svaki x njegov suprotni, tj -x, i on je između <-1,1>pa vrijedi
[latex]\sum{(-x)^n} = \frac{1}{1-(-x)}[/latex]
[latex]\sum{(-1)^n \cdot x^n} = \frac{1}{1+x}[/latex].
Sad to integriramo pa dobijemo
[latex]\sum{\frac{(-1)^n}{n+1} \cdot x^{n+1}} = ln(1+x)[/latex]
u svim ovim sumama n ide od 0 nadalje, još možeš pomaknut da ide od 1 pa se onda smanje svi n-ovi u sumi za 1...
I sad je razvoj fje f(x)=ln(1+x) onaj gore, radijus konv je <-1,1> (jer je to za geom red od kojeg smo krenuli).
Sve razvoje svih fja se dobiju iz geom reda i reda za e^x, samo se igraš sa derivacijama i integriranjem... to se dosta koristi u diskretnoj mat na 2.god pa se igraj :D
| Atomised (napisa): |
2) Taylorovi redovi.  Moram li učiti razvoj (i konvergenciju) svake funkcije posebno, postoji li neka šablona, ili se od mene očekuje da ne učim ništa napamet nego iz svih onih teorema sam zaključujem? Recimo, za e na iks sve shvaćam ali već za ln(1+x) mi nije jasno što je tu uopće razvoj, što je dokaz konvergencije i što se dobije odakle i zašto. Moram li učiti razvoj (i konvergenciju) svake funkcije posebno, postoji li neka šablona, ili se od mene očekuje da ne učim ništa napamet nego iz svih onih teorema sam zaključujem? Recimo, za e na iks sve shvaćam ali već za ln(1+x) mi nije jasno što je tu uopće razvoj, što je dokaz konvergencije i što se dobije odakle i zašto.
Hvala.  |
Najprije da ispravim aryu, θ je iz [0,1], a ne θx 
A redovi su super   
Imaš iz onih tm da se redovi dobro ponašaju na deriviranje, integriranje, zbrajanje i sl. pa sve dobivaš iz toga. Za ln(1+x) kreneš od geom reda.
Dakle znamo da je
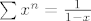 za x iz ←1,1> za x iz ←1,1>
sad uzmemo za svaki x njegov suprotni, tj -x, i on je između ←1,1>pa vrijedi
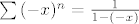
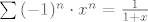 . .
Sad to integriramo pa dobijemo
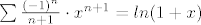
u svim ovim sumama n ide od 0 nadalje, još možeš pomaknut da ide od 1 pa se onda smanje svi n-ovi u sumi za 1...
I sad je razvoj fje f(x)=ln(1+x) onaj gore, radijus konv je ←1,1> (jer je to za geom red od kojeg smo krenuli).
Sve razvoje svih fja se dobiju iz geom reda i reda za e^x, samo se igraš sa derivacijama i integriranjem... to se dosta koristi u diskretnoj mat na 2.god pa se igraj 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 13:10 pon, 25. 8. 2008 Naslov: Postano: 13:10 pon, 25. 8. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Najprije da ispravim aryu, θ je iz [0,1], a ne θx :D[/quote]
Ma ovo x je indeks. :)
[quote="Luuka"]
I sad je razvoj fje f(x)=ln(1+x) onaj gore, radijus konv je <-1,1> (jer je to za geom red od kojeg smo krenuli).
[/quote]
Prvo, hvala na trudu i dobrom objašnjenju. :D
Ako sam dobro shvatio, prvo smo funkciju derivirali i zapisali kao red a zatim integrirali taj red član po član (i eventualno malo promijenili indekse), a radijus konvergencije dobro podnosi takve stvari pa je ostao isti. Sad, možda zvuči glupo, ali nije mi još jasno zašto je to što smo dobili Taylorov (a ne neki drugi) red?
Edit: Shvatio sam... :roll: :D
| Luuka (napisa): | Najprije da ispravim aryu, θ je iz [0,1], a ne θx  |
Ma ovo x je indeks. 
| Luuka (napisa): |
I sad je razvoj fje f(x)=ln(1+x) onaj gore, radijus konv je ←1,1> (jer je to za geom red od kojeg smo krenuli).
|
Prvo, hvala na trudu i dobrom objašnjenju. 
Ako sam dobro shvatio, prvo smo funkciju derivirali i zapisali kao red a zatim integrirali taj red član po član (i eventualno malo promijenili indekse), a radijus konvergencije dobro podnosi takve stvari pa je ostao isti. Sad, možda zvuči glupo, ali nije mi još jasno zašto je to što smo dobili Taylorov (a ne neki drugi) red?
Edit: Shvatio sam...  
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 16:42 pon, 25. 8. 2008 Naslov: Re: Nekoliko teorijskih pitanja Postano: 16:42 pon, 25. 8. 2008 Naslov: Re: Nekoliko teorijskih pitanja |
    |
|
|
[quote="Luuka"]
...fije [latex]\ln(1+x)[/latex]..., ...radijus konv je [latex]\langle -1,1][/latex] [/quote]
Ne moras uciti razvoj (prikladne) fije u red "napamet", koeficijente dobijes;
[latex]a_n=\frac{f^{(n)}(x_0)}{n!}[/latex], oko neke tocke [latex]x_0[/latex]. Naravno, ovo najcesce funkcionira, tako da si ustanovio da se fija moze razviti u red potencija na nekom skupu (ali ti se ionako u 99% slucajeva susreces sa analitickim funkcijama, pa nije bed ).
| Luuka (napisa): |
...fije 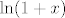 ..., ...radijus konv je ..., ...radijus konv je 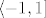 |
Ne moras uciti razvoj (prikladne) fije u red "napamet", koeficijente dobijes;
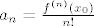 , oko neke tocke , oko neke tocke  . Naravno, ovo najcesce funkcionira, tako da si ustanovio da se fija moze razviti u red potencija na nekom skupu (ali ti se ionako u 99% slucajeva susreces sa analitickim funkcijama, pa nije bed ). . Naravno, ovo najcesce funkcionira, tako da si ustanovio da se fija moze razviti u red potencija na nekom skupu (ali ti se ionako u 99% slucajeva susreces sa analitickim funkcijama, pa nije bed ).
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 13:00 sri, 27. 8. 2008 Naslov: Postano: 13:00 sri, 27. 8. 2008 Naslov: |
    |
|
|
Mene bi zanimalo objasnjenje primjera 6.7(str. 159. ili 167.) iz skripte, pita se za konvergenciju reda 1/n*n, te se to objasnjava sa lemom prije primjera... al mi nesto nije jasno, 1/n*n > 1/(n+1)*(n+1), a u primjeru se dokaze konvg. reda 1/(n+1)*(n+1), sto mi onda garantira da i red 1/n*n konvergira? kad je on uvijek veci?
Mene bi zanimalo objasnjenje primjera 6.7(str. 159. ili 167.) iz skripte, pita se za konvergenciju reda 1/n*n, te se to objasnjava sa lemom prije primjera... al mi nesto nije jasno, 1/n*n > 1/(n+1)*(n+1), a u primjeru se dokaze konvg. reda 1/(n+1)*(n+1), sto mi onda garantira da i red 1/n*n konvergira? kad je on uvijek veci?
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
arya
Forumaš(ica)


Pridružen/a: 30. 11. 2006. (20:10:37)
Postovi: (233)16
Spol: 
Lokacija: forum
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
lajka
Forumaš(ica)


Pridružen/a: 13. 02. 2008. (23:00:13)
Postovi: (39)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
|












