| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 18:45 ned, 9. 11. 2008 Naslov: Zadatak- sa dvije zvjezdice :) Postano: 18:45 ned, 9. 11. 2008 Naslov: Zadatak- sa dvije zvjezdice :) |
    |
|
|
e, imam zadatak jedan iz skripti profesora Antonića, označen je s dvije zvjezdice, to vald znači da je mal puno teži:) zanima me kak bi ga trebalo riješit. ovak ide zadatak, direktni copy-paste:
4.¤¤ Stranice pravilnog 2n-terokuta su obojene crveno i plavo u nekom poretku. Korak je postupak
bojenja svake stranice kojoj su susjedne stranice iste boje u crveno i bojenja ostalih stranica u
plavo. Dokaˇzite da ´ce nakon 2n−1 koraka sve stranice biti obojene u crveno.
ustvari, da, to treba dokazati. jel to ide indukcijom il šta, neam pojma. hvala unaprijed odazvanim umovima:)
e, imam zadatak jedan iz skripti profesora Antonića, označen je s dvije zvjezdice, to vald znači da je mal puno teži zanima me kak bi ga trebalo riješit. ovak ide zadatak, direktni copy-paste: zanima me kak bi ga trebalo riješit. ovak ide zadatak, direktni copy-paste:
4.¤¤ Stranice pravilnog 2n-terokuta su obojene crveno i plavo u nekom poretku. Korak je postupak
bojenja svake stranice kojoj su susjedne stranice iste boje u crveno i bojenja ostalih stranica u
plavo. Dokaˇzite da ´ce nakon 2n−1 koraka sve stranice biti obojene u crveno.
ustvari, da, to treba dokazati. jel to ide indukcijom il šta, neam pojma. hvala unaprijed odazvanim umovima:)
|
|
| [Vrh] |
|
Tvrtko
Forumaš(ica)

Pridružen/a: 21. 10. 2006. (12:12:34)
Postovi: (10A)16
Lokacija: CCP 4345 / PMF-MO 225
|
 Postano: 22:27 ned, 9. 11. 2008 Naslov: Postano: 22:27 ned, 9. 11. 2008 Naslov: |
    |
|
|
Kad sam bio demos iz LA radio sam na priredjivanju zadataka za studente, pa sam tako dodao taj zadatak u te zadatke. (Vidio sam ga negdje i svidio mi se pa sam pitao mogu li ga dodat i receno je da mogu.)
Dakle dokaz ide na sljedeci nacin. (Usput rijec je o potencijama ako se nevaram tj. [latex]2^n[/latex]-terokut je u pitanju i slicno.)
S [latex]{\bf a}_k\in {\rm M}_{2^{n}\times 1}(\mathbb{Z})[/latex] oznacavmo vektor stupac, koji nam govori o bojama stranica ovog mnogokuta. U i-tom retku je paran broj ako je i-ta stranica u k-tom trenutku crvena, ako je neparan broj onda je plave boje.
Pocetno stanje zapisemo nulama i jedinicama u vektor [latex]{\bf a}_0[/latex].
Sada trebas naci matricu [latex]{\bf P}\in {\rm M}_{2^n\times 2^n}[/latex] takvu da je [latex]{\bf a}_k={\bf P}^{k}{\bf a}_0[/latex]. Sve što ti moraš dokazati je da je [latex]{\bf P}^{2^{n}-1}{\bf a}_0[/latex] vektor stupac kojem su svi elementi parni brojevi.
Ovo pricam napamet, pa je moguce da nesto nisam tocno napisao, ali ovako dokaz ide.
Kad sam bio demos iz LA radio sam na priredjivanju zadataka za studente, pa sam tako dodao taj zadatak u te zadatke. (Vidio sam ga negdje i svidio mi se pa sam pitao mogu li ga dodat i receno je da mogu.)
Dakle dokaz ide na sljedeci nacin. (Usput rijec je o potencijama ako se nevaram tj. 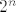 -terokut je u pitanju i slicno.) -terokut je u pitanju i slicno.)
S 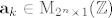 oznacavmo vektor stupac, koji nam govori o bojama stranica ovog mnogokuta. U i-tom retku je paran broj ako je i-ta stranica u k-tom trenutku crvena, ako je neparan broj onda je plave boje. oznacavmo vektor stupac, koji nam govori o bojama stranica ovog mnogokuta. U i-tom retku je paran broj ako je i-ta stranica u k-tom trenutku crvena, ako je neparan broj onda je plave boje.
Pocetno stanje zapisemo nulama i jedinicama u vektor 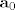 . .
Sada trebas naci matricu 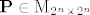 takvu da je takvu da je 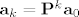 . Sve što ti moraš dokazati je da je . Sve što ti moraš dokazati je da je 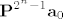 vektor stupac kojem su svi elementi parni brojevi. vektor stupac kojem su svi elementi parni brojevi.
Ovo pricam napamet, pa je moguce da nesto nisam tocno napisao, ali ovako dokaz ide.
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
|







