| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zebrica
Forumaš(ica)
Pridružen/a: 06. 09. 2008. (09:22:46)
Postovi: (2F)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
zebrica
Forumaš(ica)
Pridružen/a: 06. 09. 2008. (09:22:46)
Postovi: (2F)16
|
 Postano: 21:14 sri, 10. 12. 2008 Naslov: Postano: 21:14 sri, 10. 12. 2008 Naslov: |
    |
|
|
trebam odrediti a, b i c za općenite podatke (x1, y1),...,(xn,yn)
na vjezbama smo za fju y=ax+b a i b izrazili pomoću kovarijanci pa me to mući
trebam odrediti a, b i c za općenite podatke (x1, y1),...,(xn,yn)
na vjezbama smo za fju y=ax+b a i b izrazili pomoću kovarijanci pa me to mući
|
|
| [Vrh] |
|
teddybear
Forumaš(ica)


Pridružen/a: 01. 03. 2008. (09:23:58)
Postovi: (7)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 20:16 ned, 14. 12. 2008 Naslov: Postano: 20:16 ned, 14. 12. 2008 Naslov: |
    |
|
|
[quote="teddybear"]mene pak zanima da li ako znam da je sigma kovarijaciska matrica vektora koji je n-dimenzionalan s normalnom razdiobom uglavnom ako je ta matrica pozitivno definitna. Ja je dakle mogu napisati kao A puta A transponirano. Zanima me da li ta matrica A mora bit matrica tip nxn ili ne? Od nekud bih trebala izvuci to da je bas nxn jer sam to pretpostavila i tak izracunala, a jedino neiskoristeno mi je ostala ta pozitivna definitnost :roll: kad ga namjestam :D
i sorry ali imam skroz drugaciji zadatak pa ti ne mogu pomoci[/quote]
Kovarijacijska matrica nemora biti pozitivno definitna, ali je uvijek pozitivno semidefinitna. Ako je još i pozitivno definitna, onda se radi o neprekidnoj višedimenzionalnoj normalnoj razdiobi.
I ne mora biti kvadratna, A može bit mxn matrica i kovarijacijska matrica je pozitivno definitna akko je A punog ranga (rečanog ili stupčanog)
Ak nekom treba pomoć oko zadaće, može mi se javit na alen.lancic na gmailu u vezi pojedinosti
| teddybear (napisa): | mene pak zanima da li ako znam da je sigma kovarijaciska matrica vektora koji je n-dimenzionalan s normalnom razdiobom uglavnom ako je ta matrica pozitivno definitna. Ja je dakle mogu napisati kao A puta A transponirano. Zanima me da li ta matrica A mora bit matrica tip nxn ili ne? Od nekud bih trebala izvuci to da je bas nxn jer sam to pretpostavila i tak izracunala, a jedino neiskoristeno mi je ostala ta pozitivna definitnost  kad ga namjestam kad ga namjestam 
i sorry ali imam skroz drugaciji zadatak pa ti ne mogu pomoci |
Kovarijacijska matrica nemora biti pozitivno definitna, ali je uvijek pozitivno semidefinitna. Ako je još i pozitivno definitna, onda se radi o neprekidnoj višedimenzionalnoj normalnoj razdiobi.
I ne mora biti kvadratna, A može bit mxn matrica i kovarijacijska matrica je pozitivno definitna akko je A punog ranga (rečanog ili stupčanog)
Ak nekom treba pomoć oko zadaće, može mi se javit na alen.lancic na gmailu u vezi pojedinosti
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
Lara
Forumaš(ica)


Pridružen/a: 17. 01. 2007. (16:23:54)
Postovi: (53)16
Spol: 
|
 Postano: 22:30 pon, 23. 11. 2009 Naslov: Re: pomoc oko zadace Postano: 22:30 pon, 23. 11. 2009 Naslov: Re: pomoc oko zadace |
    |
|
|
[quote="zebrica"]trebam aproksimirat podatke funkcijom y=asinx+bcosx+c metodom najmanjih kvadrata
mogu li ja parametre izrazit pomocu sume sinxi i slično ili postoji neka caka kako se rijesiti sin i cos?[/quote]
Mene kod ovakvih zadataka zanima sljedece:
Ako definiram funkciju L(a,b,c) koju hocu minimizirati, dakle sve standardno i zatim dobijem sustave i zapisem to matricno. Da bi dobila rjesenje trebala bi naci inverz matrice sustava. No, kako nisu konkretni podaci zadani, ta matrice bi za elemente imala sume potencija od x-eva. Kako onda tome naci inverz? Ili se to samo napise x=(A na -1) * y. Razumije li me se uopce? :?
Jel se to tako moze uopce? Imam i drugi pristup za slucaj da ovako nije idealno, ali ovo me zanima:)
| zebrica (napisa): | trebam aproksimirat podatke funkcijom y=asinx+bcosx+c metodom najmanjih kvadrata
mogu li ja parametre izrazit pomocu sume sinxi i slično ili postoji neka caka kako se rijesiti sin i cos? |
Mene kod ovakvih zadataka zanima sljedece:
Ako definiram funkciju L(a,b,c) koju hocu minimizirati, dakle sve standardno i zatim dobijem sustave i zapisem to matricno. Da bi dobila rjesenje trebala bi naci inverz matrice sustava. No, kako nisu konkretni podaci zadani, ta matrice bi za elemente imala sume potencija od x-eva. Kako onda tome naci inverz? Ili se to samo napise x=(A na -1) * y. Razumije li me se uopce? 
Jel se to tako moze uopce? Imam i drugi pristup za slucaj da ovako nije idealno, ali ovo me zanima:)
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
 Postano: 12:18 uto, 24. 11. 2009 Naslov: Re: pomoc oko zadace Postano: 12:18 uto, 24. 11. 2009 Naslov: Re: pomoc oko zadace |
    |
|
|
[quote="Lara"][quote="zebrica"]trebam aproksimirat podatke funkcijom y=asinx+bcosx+c metodom najmanjih kvadrata
mogu li ja parametre izrazit pomocu sume sinxi i slično ili postoji neka caka kako se rijesiti sin i cos?[/quote]
Mene kod ovakvih zadataka zanima sljedece:
Ako definiram funkciju L(a,b,c) koju hocu minimizirati, dakle sve standardno i zatim dobijem sustave i zapisem to matricno. Da bi dobila rjesenje trebala bi naci inverz matrice sustava. No, kako nisu konkretni podaci zadani, ta matrice bi za elemente imala sume potencija od x-eva. Kako onda tome naci inverz? Ili se to samo napise x=(A na -1) * y. Razumije li me se uopce? :?
Jel se to tako moze uopce? Imam i drugi pristup za slucaj da ovako nije idealno, ali ovo me zanima:)[/quote]
Mislim da je fora upravo u tome da zakljucis za koje vrijednosti x_i-eva je matrica sustava regularna...bar sam ja tako napravio :D
pitat cu jos profesora sutra...
| Lara (napisa): | | zebrica (napisa): | trebam aproksimirat podatke funkcijom y=asinx+bcosx+c metodom najmanjih kvadrata
mogu li ja parametre izrazit pomocu sume sinxi i slično ili postoji neka caka kako se rijesiti sin i cos? |
Mene kod ovakvih zadataka zanima sljedece:
Ako definiram funkciju L(a,b,c) koju hocu minimizirati, dakle sve standardno i zatim dobijem sustave i zapisem to matricno. Da bi dobila rjesenje trebala bi naci inverz matrice sustava. No, kako nisu konkretni podaci zadani, ta matrice bi za elemente imala sume potencija od x-eva. Kako onda tome naci inverz? Ili se to samo napise x=(A na -1) * y. Razumije li me se uopce? 
Jel se to tako moze uopce? Imam i drugi pristup za slucaj da ovako nije idealno, ali ovo me zanima:) |
Mislim da je fora upravo u tome da zakljucis za koje vrijednosti x_i-eva je matrica sustava regularna...bar sam ja tako napravio 
pitat cu jos profesora sutra...
|
|
| [Vrh] |
|
Lara
Forumaš(ica)


Pridružen/a: 17. 01. 2007. (16:23:54)
Postovi: (53)16
Spol: 
|
 Postano: 12:54 uto, 24. 11. 2009 Naslov: Re: pomoc oko zadace Postano: 12:54 uto, 24. 11. 2009 Naslov: Re: pomoc oko zadace |
    |
|
|
[quote="behemont"][quote="Lara"][quote="zebrica"]trebam aproksimirat podatke funkcijom y=asinx+bcosx+c metodom najmanjih kvadrata
mogu li ja parametre izrazit pomocu sume sinxi i slično ili postoji neka caka kako se rijesiti sin i cos?[/quote]
Mene kod ovakvih zadataka zanima sljedece:
Ako definiram funkciju L(a,b,c) koju hocu minimizirati, dakle sve standardno i zatim dobijem sustave i zapisem to matricno. Da bi dobila rjesenje trebala bi naci inverz matrice sustava. No, kako nisu konkretni podaci zadani, ta matrice bi za elemente imala sume potencija od x-eva. Kako onda tome naci inverz? Ili se to samo napise x=(A na -1) * y. Razumije li me se uopce? :?
Jel se to tako moze uopce? Imam i drugi pristup za slucaj da ovako nije idealno, ali ovo me zanima:)[/quote]
Mislim da je fora upravo u tome da zakljucis za koje vrijednosti x_i-eva je matrica sustava regularna...bar sam ja tako napravio :D
pitat cu jos profesora sutra...[/quote]
Da, i ja sam zakljucila za koje vrijednost je matrica regularna. I znam kad postoji jedinstveno rješenje. No, sad za to rjesenje izrazeno pomocu inverza neke matrice treba raditi rastav varijace. Nekako mi to sve skupa izgleda gadno. Ali to je to, jel?
| behemont (napisa): | | Lara (napisa): | | zebrica (napisa): | trebam aproksimirat podatke funkcijom y=asinx+bcosx+c metodom najmanjih kvadrata
mogu li ja parametre izrazit pomocu sume sinxi i slično ili postoji neka caka kako se rijesiti sin i cos? |
Mene kod ovakvih zadataka zanima sljedece:
Ako definiram funkciju L(a,b,c) koju hocu minimizirati, dakle sve standardno i zatim dobijem sustave i zapisem to matricno. Da bi dobila rjesenje trebala bi naci inverz matrice sustava. No, kako nisu konkretni podaci zadani, ta matrice bi za elemente imala sume potencija od x-eva. Kako onda tome naci inverz? Ili se to samo napise x=(A na -1) * y. Razumije li me se uopce? 
Jel se to tako moze uopce? Imam i drugi pristup za slucaj da ovako nije idealno, ali ovo me zanima:) |
Mislim da je fora upravo u tome da zakljucis za koje vrijednosti x_i-eva je matrica sustava regularna...bar sam ja tako napravio 
pitat cu jos profesora sutra... |
Da, i ja sam zakljucila za koje vrijednost je matrica regularna. I znam kad postoji jedinstveno rješenje. No, sad za to rjesenje izrazeno pomocu inverza neke matrice treba raditi rastav varijace. Nekako mi to sve skupa izgleda gadno. Ali to je to, jel?
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 19:25 sri, 25. 11. 2009 Naslov: Postano: 19:25 sri, 25. 11. 2009 Naslov: |
    |
|
|
Funkcija [latex]x\rightarrow -\operatorname{ln}x[/latex] je konveksna, iz Jensenove nejedankost slijedi, [latex]\leq[/latex] nejednakost, a stroga nejednakost slijedi iz uvjeta nedegeneriranosti.
Edit1: Sorry, ovo nije tocno. Budem kasnije postao rijesenje.
Edit2: Evo, sada je tocno.
Funkcija 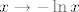 je konveksna, iz Jensenove nejedankost slijedi, je konveksna, iz Jensenove nejedankost slijedi, 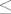 nejednakost, a stroga nejednakost slijedi iz uvjeta nedegeneriranosti. nejednakost, a stroga nejednakost slijedi iz uvjeta nedegeneriranosti.
Edit1: Sorry, ovo nije tocno. Budem kasnije postao rijesenje.
Edit2: Evo, sada je tocno.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Lara
Forumaš(ica)


Pridružen/a: 17. 01. 2007. (16:23:54)
Postovi: (53)16
Spol: 
|
 Postano: 0:33 čet, 26. 11. 2009 Naslov: Postano: 0:33 čet, 26. 11. 2009 Naslov: |
    |
|
|
[quote="zebrica"]trebam aproksimirat podatke funkcijom y=asinx+bcosx+c metodom najmanjih kvadrata
mogu li ja parametre izrazit pomocu sume sinxi i slično ili postoji neka caka kako se rijesiti sin i cos?[/quote]
Jel bi mi mogao netko pomoci kako da nadjem rastav varijance za ovakve zadatke? Znam da Vam puno ima takav zadatak, zato... :D
Zapravo me zanima interpretacija rastava varijance, sto mi tu uopce radimo? Vidjela sam one neke formule, ok, nije problem uvrstiti, no necu dobiti nista pametno jer su mi ionako procijenjeni parametri izrazeni u obliku koji nije pogodan za daljni rad s njima.
Uglavnom, ako bi mi netko pojasnio sto je to rastav varijance bila bi ful zahvalna;)
[size=9][color=#999999]Added after 44 minutes:[/color][/size]
http://degiorgi.math.hr/aktuari/doc/vms.pdf
Ima na 92. stranici vrlo lijepo pojašnjeno ono sto sam ja pitala...
| zebrica (napisa): | trebam aproksimirat podatke funkcijom y=asinx+bcosx+c metodom najmanjih kvadrata
mogu li ja parametre izrazit pomocu sume sinxi i slično ili postoji neka caka kako se rijesiti sin i cos? |
Jel bi mi mogao netko pomoci kako da nadjem rastav varijance za ovakve zadatke? Znam da Vam puno ima takav zadatak, zato... 
Zapravo me zanima interpretacija rastava varijance, sto mi tu uopce radimo? Vidjela sam one neke formule, ok, nije problem uvrstiti, no necu dobiti nista pametno jer su mi ionako procijenjeni parametri izrazeni u obliku koji nije pogodan za daljni rad s njima.
Uglavnom, ako bi mi netko pojasnio sto je to rastav varijance bila bi ful zahvalna;)
Added after 44 minutes:
http://degiorgi.math.hr/aktuari/doc/vms.pdf
Ima na 92. stranici vrlo lijepo pojašnjeno ono sto sam ja pitala...
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
|
| [Vrh] |
|
|













