| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
filipnet
Forumaš(ica)
Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
 Postano: 20:27 pet, 9. 1. 2009 Naslov: pomoc oko sume |
    |
|
|
Imam jednu malo ne jasnocu sa jednim zadatakom iz jednog starog pismenog, imam rjesenja, ali mi nije jasan jedan korak
zadatak: suma(k=0,n)[(n povrh k)/(2n-1 povrh k)
kad se to lijepo raspise dode se do jednog koraka
n!(n-1)!/(2n-1)!*suma(k=0, n)(n-1+l povrh l)=n!(n-1)!/(2n-1)!*(2n povrh n)
kud je nestala suma, prvo sam mislio da je to parcijalna sumacija, ali nikak da dobijem to, pa moze mala pomoc?
Fala!
Imam jednu malo ne jasnocu sa jednim zadatakom iz jednog starog pismenog, imam rjesenja, ali mi nije jasan jedan korak
zadatak: suma(k=0,n)[(n povrh k)/(2n-1 povrh k)
kad se to lijepo raspise dode se do jednog koraka
n!(n-1)!/(2n-1)!*suma(k=0, n)(n-1+l povrh l)=n!(n-1)!/(2n-1)!*(2n povrh n)
kud je nestala suma, prvo sam mislio da je to parcijalna sumacija, ali nikak da dobijem to, pa moze mala pomoc?
Fala!
_________________  Everything happens with a reason! 
 |
|
| [Vrh] |
|
duje
Forumaš(ica)
Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol:
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)
Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol:
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)
Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol:
Lokacija: cvrsto na stolici
|
| Postano: 21:39 ned, 11. 1. 2009 Naslov: |
|
|
|
da ne otvaram novi topic, opet imam jedan problem sa sumo, tj. nejasnocu.
ovo je zadatak iz vjezbi
suma(k=0, n) (n povrh k) k! 1/(n+k+1)!, n>=0
to se fino raspise i dodemo do jednog koraka
n!/(2n+1)! *suma(k=0, n) (2n+1 povrh l)
sljedece pise =simetrija=n!/(2n+1)! *1/2*suma(k=0, 2n+1) (2n+1 povrh l)
ne kuzim kak smo dobili ovih 1/2 i zasto suma sada ide do 2n+1? moze mala pomoc? fala unaprijded!
da ne otvaram novi topic, opet imam jedan problem sa sumo, tj. nejasnocu.
ovo je zadatak iz vjezbi
suma(k=0, n) (n povrh k) k! 1/(n+k+1)!, n>=0
to se fino raspise i dodemo do jednog koraka
n!/(2n+1)! *suma(k=0, n) (2n+1 povrh l)
sljedece pise =simetrija=n!/(2n+1)! *1/2*suma(k=0, 2n+1) (2n+1 povrh l)
ne kuzim kak smo dobili ovih 1/2 i zasto suma sada ide do 2n+1? moze mala pomoc? fala unaprijded!
_________________ Everything happens with a reason!
|
|
| [Vrh] |
|
nlo
Forumaš(ica)
Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)
Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol:
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
nlo
Forumaš(ica)
Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)
Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol:
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)
Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol:
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)
Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol:
Lokacija: cvrsto na stolici
|
| Postano: 19:23 uto, 13. 1. 2009 Naslov: |
|
|
|
Opet ja. Trebam pomoc oko jednog zadatka, imam rjesenje za njega ali sam zapeo na jednom dijelu:
[latex]\displaystyle \sum_{k=1}^{n}\frac{ k^2+k-1 }{(k+2)!}=\sum_{k=1}^{n}\frac{ k(k+2)-(k+1)}{ (k+2)!}=\sum_{k=1}^{n}\frac{ k}{(k+1)!}-\frac{(k+1)}{ (k+2)!}[/latex], do tud sve kuzim, ali onda pise u rjesenju ovo, a to mi nije najjasnije kak smo dobili, a znam da je nesto jednostavno.
[latex]\displaystyle \frac{1}{2}-\frac{n+1}{(n+2)!}[/latex]
kako smo se rijesili sume?
Opet ja. Trebam pomoc oko jednog zadatka, imam rjesenje za njega ali sam zapeo na jednom dijelu:
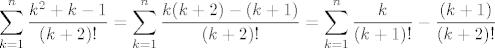 , do tud sve kuzim, ali onda pise u rjesenju ovo, a to mi nije najjasnije kak smo dobili, a znam da je nesto jednostavno.
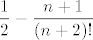
kako smo se rijesili sume?
_________________ Everything happens with a reason!
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)
Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
tperkov
Forumaš(ica)
Pridružen/a: 08. 12. 2008. (15:17:18)
Postovi: (71)16
|
| Postano: 20:37 uto, 13. 1. 2009 Naslov: |
|
|
|
[quote="filipnet"]Opet ja. Trebam pomoc oko jednog zadatka, imam rjesenje za njega ali sam zapeo na jednom dijelu:
[latex]\displaystyle \sum_{k=1}^{n}\frac{ k^2+k-1 }{(k+2)!}=\sum_{k=1}^{n}\frac{ k(k+2)-(k+1)}{ (k+2)!}=\sum_{k=1}^{n}\frac{ k}{(k+1)!}-\frac{(k+1)}{ (k+2)!}[/latex], do tud sve kuzim, ali onda pise u rjesenju ovo, a to mi nije najjasnije kak smo dobili, a znam da je nesto jednostavno.
[latex]\displaystyle \frac{1}{2}-\frac{n+1}{(n+2)!}[/latex]
kako smo se rijesili sume?[/quote]
uvijek prvo probaj malo raspisati sumu, pa ćeš i sam odmah sve vidjeti
| filipnet (napisa): | Opet ja. Trebam pomoc oko jednog zadatka, imam rjesenje za njega ali sam zapeo na jednom dijelu:
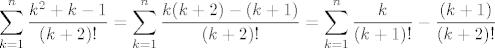, do tud sve kuzim, ali onda pise u rjesenju ovo, a to mi nije najjasnije kak smo dobili, a znam da je nesto jednostavno.
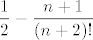
kako smo se rijesili sume? |
uvijek prvo probaj malo raspisati sumu, pa ćeš i sam odmah sve vidjeti
|
|
| [Vrh] |
|
|
