| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 23:57 pon, 2. 2. 2009 Naslov: Postano: 23:57 pon, 2. 2. 2009 Naslov: |
    |
|
|
Ne znam jesi već i sam riješio, ali tek sam sad vidio da pitaš.
Uglavnom, neka je [latex]h\in H[/latex] i neka je [latex]r[/latex] red tog elementa, a neka je [latex]s[/latex] red elementa [latex]hN[/latex] u grupi [latex]G/N[/latex]. Tad je [latex](hN)^r=h^rN=N[/latex] pa zaključujemo da [latex]s \big| r[/latex]. Međutim, [latex]r \big| \lvert H \rvert[/latex] pa [latex]s \big| \lvert H \rvert[/latex]. Zbog [latex]s \big| \lvert G/N \rvert=[G:N][/latex] i činjenice da su [latex][G:N][/latex] i [latex]\lvert H \rvert[/latex] relativno prosti, imamo [latex]s=1[/latex], tj. [latex]hN=N[/latex]. No tad je [latex]h\in N[/latex].
Ne znam jesi već i sam riješio, ali tek sam sad vidio da pitaš.
Uglavnom, neka je 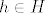 i neka je i neka je  red tog elementa, a neka je red tog elementa, a neka je  red elementa red elementa 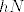 u grupi u grupi 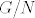 . Tad je . Tad je 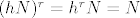 pa zaključujemo da pa zaključujemo da 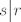 . Međutim, . Međutim, 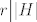 pa pa 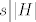 . Zbog . Zbog 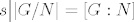 i činjenice da su i činjenice da su 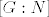 i i 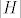 relativno prosti, imamo relativno prosti, imamo 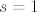 , tj. , tj. 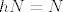 . No tad je . No tad je 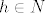 . .
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
 Postano: 22:51 uto, 10. 2. 2009 Naslov: Postano: 22:51 uto, 10. 2. 2009 Naslov: |
    |
|
|
To je posebni slučaj teorema da je svaka podgrupa cikličke grupe također ciklička.
Ideja je ova: ako je G = <a> i H < G, neka je a^m takav elemant od H, različit od 1, da je m minimalan. Onda se pokaže da je H = <a^m>.
Naime, neka je b iz H, onda je b= a^k, jer je iz G, i također oblika b = a^(mq + r), gdje je r ostatak pri dijeljenju k s m. Sada, b je iz H kao i
a^(mq) pa onda i a^r mora biti iz H, ali zbog minimalnosti m mora biti r = 0 pa je i b iz cikličke podgrupe generiran s a^m i to je onda cijela H.
To je posebni slučaj teorema da je svaka podgrupa cikličke grupe također ciklička.
Ideja je ova: ako je G = <a> i H < G, neka je a^m takav elemant od H, različit od 1, da je m minimalan. Onda se pokaže da je H = <a^m>.
Naime, neka je b iz H, onda je b= a^k, jer je iz G, i također oblika b = a^(mq + r), gdje je r ostatak pri dijeljenju k s m. Sada, b je iz H kao i
a^(mq) pa onda i a^r mora biti iz H, ali zbog minimalnosti m mora biti r = 0 pa je i b iz cikličke podgrupe generiran s a^m i to je onda cijela H.
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 15:26 ned, 15. 2. 2009 Naslov: Postano: 15:26 ned, 15. 2. 2009 Naslov: |
    |
|
|
Neka je [latex]x\in H[/latex]. Pogledaj niz elemenata iz [latex]H[/latex]:
[latex]x, x^2, x^3, \ldots[/latex]
Budući da je [latex]H[/latex] konačan, ne mogu svi biti različiti, tj. postoje pozitivni prirodni brojevi [latex]m[/latex] i [latex]n[/latex], [latex]m<n[/latex], takvi da je [latex]x^m=x^n[/latex]. Pokaži da je [latex]x^{n-m-1}\in H[/latex] i da je upravo to inverz od [latex]x[/latex].
Neka je 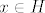 . Pogledaj niz elemenata iz . Pogledaj niz elemenata iz 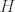 : :
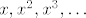
Budući da je 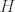 konačan, ne mogu svi biti različiti, tj. postoje pozitivni prirodni brojevi konačan, ne mogu svi biti različiti, tj. postoje pozitivni prirodni brojevi  i i  , , 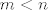 , takvi da je , takvi da je 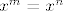 . Pokaži da je . Pokaži da je 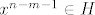 i da je upravo to inverz od i da je upravo to inverz od  . .
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 15:34 uto, 17. 2. 2009 Naslov: Postano: 15:34 uto, 17. 2. 2009 Naslov: |
    |
|
|
[quote="Braslav"]Zadatak... Neka je [latex]|G|=p^{n}[/latex] , tada za svaki k = 0, 1, ..., n postoji podgrupa H reda k. takva da je normalna u G. Molim pomoc.[/quote]
Čudno. Langrangeov teorem kaže da red konačne podgrupe dijeli red grupe. Pa onda podgrupa H može eventualno biti reda [latex]p^{k}[/latex]
Edit: pretpostavio sam da je [latex]p[/latex] prost broj, zbog sugestivne oznake..
| Braslav (napisa): | Zadatak... Neka je 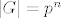 , tada za svaki k = 0, 1, ..., n postoji podgrupa H reda k. takva da je normalna u G. Molim pomoc. , tada za svaki k = 0, 1, ..., n postoji podgrupa H reda k. takva da je normalna u G. Molim pomoc. |
Čudno. Langrangeov teorem kaže da red konačne podgrupe dijeli red grupe. Pa onda podgrupa H može eventualno biti reda 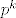
Edit: pretpostavio sam da je  prost broj, zbog sugestivne oznake.. prost broj, zbog sugestivne oznake..
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
 Postano: 13:43 pet, 20. 2. 2009 Naslov: Postano: 13:43 pet, 20. 2. 2009 Naslov: |
    |
|
|
Zadatak.... U [latex]\mathbb{Z}[[X]][/latex] je svaki maksimalan ideal oblika (p,X) gdje je p prost broj. Sada lako se pokaze da je (p,X) prost ideal, ali kako pokazati da je svaki prost ideal tog oblika?
[size=9][color=#999999]Added after 9 minutes:[/color][/size]
Mozda ovako... [latex]\mathbb{Z}[[X]]/M[/latex] je konacno polje (kako znamo da ne moze biti beskonacno?) pa je izomorfno sa [latex] \mathbb{Z}_{p}=\mathbb{Z}[[X]]/(p,X)[/latex] pa imamo da je a+M=b+(p,X)
no tada je -a+M=-b+(p,X) pa imamo M=(p,X).
Zadatak.... U 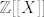 je svaki maksimalan ideal oblika (p,X) gdje je p prost broj. Sada lako se pokaze da je (p,X) prost ideal, ali kako pokazati da je svaki prost ideal tog oblika? je svaki maksimalan ideal oblika (p,X) gdje je p prost broj. Sada lako se pokaze da je (p,X) prost ideal, ali kako pokazati da je svaki prost ideal tog oblika?
Added after 9 minutes:
Mozda ovako... 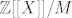 je konacno polje (kako znamo da ne moze biti beskonacno?) pa je izomorfno sa je konacno polje (kako znamo da ne moze biti beskonacno?) pa je izomorfno sa 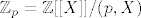 pa imamo da je a+M=b+(p,X) pa imamo da je a+M=b+(p,X)
no tada je -a+M=-b+(p,X) pa imamo M=(p,X).
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
|





















