| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 8:34 pet, 13. 2. 2009 Naslov: Postano: 8:34 pet, 13. 2. 2009 Naslov: |
    |
|
|
e da, kad ja mogu otić pos svoju duju? jel se to ide nekim redom na usmeni i po potpis il je sve stihijski?
e da, kad ja mogu otić pos svoju duju? jel se to ide nekim redom na usmeni i po potpis il je sve stihijski?
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 10:41 pet, 13. 2. 2009 Naslov: Postano: 10:41 pet, 13. 2. 2009 Naslov: |
    |
|
|
vjerojatno da će profesor reći kad može da pita, u kojim danima, satima, i to. pa će se onda ljudi trebat odlučit na koji termin doć i onda se prijavit profesoru.
vidio sam da se po potpis treba otići danas u šest navečer. al to je tek jutros stavljeno na net, čini mi se, a ja nisam u Zagrebu, neg na dobrih poprilično kilometara dalje. pa tak da mi taj termin za upis ocjena malo i ne odgovara :)
vjerojatno da će profesor reći kad može da pita, u kojim danima, satima, i to. pa će se onda ljudi trebat odlučit na koji termin doć i onda se prijavit profesoru.
vidio sam da se po potpis treba otići danas u šest navečer. al to je tek jutros stavljeno na net, čini mi se, a ja nisam u Zagrebu, neg na dobrih poprilično kilometara dalje. pa tak da mi taj termin za upis ocjena malo i ne odgovara 
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
teapot
Forumaš(ica)
Pridružen/a: 12. 02. 2009. (22:01:19)
Postovi: (36)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 13:56 pet, 13. 2. 2009 Naslov: Postano: 13:56 pet, 13. 2. 2009 Naslov: |
    |
|
|
Evo, ako nekoga zanima, ja danas odgovarao (za peticu) kod profesorice Bombardelli, profesorica zahtjeva da se gradivo zna i razumije (naglasak na razumijevanju), ali nije stroga i jako je pristupačna.
Pitanja su bila: definicija polinoma, teorem o jednakosti polinoma (dokaz), teorem o nul polinomu (dokaz), arhimedov aksiom, aksiomi polja [latex]\mathbb{R}[/latex], Peanovi aksiomi, princip matematičke indukcije, (i)reducibilnost polinoma nad [latex]\mathbb{R}[/latex] i [latex]\mathbb{C}[/latex], Bezoutov teorem (dokaz), dokaz da je skup [latex]\mathbb{R}[/latex] neprebrojiv i da ima više elemenata od skupa [latex]\mathbb{N}[/latex].
[size=1]P.S. Imam 5[/size] :yesss:
Evo, ako nekoga zanima, ja danas odgovarao (za peticu) kod profesorice Bombardelli, profesorica zahtjeva da se gradivo zna i razumije (naglasak na razumijevanju), ali nije stroga i jako je pristupačna.
Pitanja su bila: definicija polinoma, teorem o jednakosti polinoma (dokaz), teorem o nul polinomu (dokaz), arhimedov aksiom, aksiomi polja  , Peanovi aksiomi, princip matematičke indukcije, (i)reducibilnost polinoma nad , Peanovi aksiomi, princip matematičke indukcije, (i)reducibilnost polinoma nad  i i  , Bezoutov teorem (dokaz), dokaz da je skup , Bezoutov teorem (dokaz), dokaz da je skup  neprebrojiv i da ima više elemenata od skupa neprebrojiv i da ima više elemenata od skupa 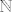 . .
P.S. Imam 5 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 14:32 pet, 13. 2. 2009 Naslov: Postano: 14:32 pet, 13. 2. 2009 Naslov: |
    |
|
|
moja pitanja su bila: definicija relacije, binarna relacija, koja svojstva ima, dal postoji relacija koja je i sim i anti sim, rel ekv, parcijalni uredaj, sto je 'znacajno' kod rel ekv... da odreduje particiju skupa ciji su elementi sve klase ekv... dokazat, teorem o djeljenju s ostatkom, Q je prebrojiv, sto je to ireducibilan polinom, napisat polinom 3st koji je negdje ireducibilan, i di
moja pitanja su bila: definicija relacije, binarna relacija, koja svojstva ima, dal postoji relacija koja je i sim i anti sim, rel ekv, parcijalni uredaj, sto je 'znacajno' kod rel ekv... da odreduje particiju skupa ciji su elementi sve klase ekv... dokazat, teorem o djeljenju s ostatkom, Q je prebrojiv, sto je to ireducibilan polinom, napisat polinom 3st koji je negdje ireducibilan, i di
_________________
Mario Berljafa
|
|
| [Vrh] |
|
PaVla
Forumaš(ica)

Pridružen/a: 18. 09. 2008. (12:04:49)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
|
| [Vrh] |
|
PaVla
Forumaš(ica)

Pridružen/a: 18. 09. 2008. (12:04:49)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
|
| [Vrh] |
|
PaVla
Forumaš(ica)

Pridružen/a: 18. 09. 2008. (12:04:49)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
uzorni student
Forumaš(ica)

Pridružen/a: 24. 01. 2009. (16:11:39)
Postovi: (2C)16
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 13:12 sub, 14. 2. 2009 Naslov: Postano: 13:12 sub, 14. 2. 2009 Naslov: |
    |
|
|
moš uzet tu trojčicu
moš uzet tu trojčicu
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
|















