| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
uzorni student
Forumaš(ica)

Pridružen/a: 24. 01. 2009. (16:11:39)
Postovi: (2C)16
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:41 ned, 15. 2. 2009 Naslov: Postano: 11:41 ned, 15. 2. 2009 Naslov: |
    |
|
|
Prvo pokažemo da su [latex]\mathbb{N}[/latex] i [latex]\mathbb{N} \times \mathbb{N}[/latex] ekvipotentni:
Očito je da za svaki [latex]n \in \mathbb{N}[/latex] postoji [b]jedinstveni[/b] [latex]r \in \mathbb{N}[/latex] takav da je
[latex]\frac{r\left(r-1\right)}{2} < n \leq \frac{r\left(r+1\right)}{2}[/latex].
Dalje, želimo konstruirati [b]bijekciju[/b] s [latex]\mathbb{N}[/latex] na [latex]\mathbb{N} \times \mathbb{N}[/latex]. U skupu [latex]\mathbb{N} \times \mathbb{N}[/latex] se nalaze uređeni parovi. Neka je uređeni par jednak [latex]\left(p,\,q\right)[/latex]. Lako je za vidjeti da (različitih) uređenih parova za koje je [latex]p+q=k[/latex], za neki [latex]k \in \mathbb{N} \setminus \left\{1\right\}[/latex] ima točno [latex]k-1[/latex].
Sada ćemo za svaki [latex]r \in \mathbb{N}[/latex] onim prirodnim [latex]n[/latex]-ovima za koje je [latex]\frac{r\left(r-1\right)}{2} < n \leq \frac{r\left(r+1\right)}{2}[/latex] [b]bijektivno[/b] pridružiti uređen par [latex]\left(p,\,q\right)[/latex] i to takav da je [latex]p+q=r+1[/latex]. Na taj ćemo način pogoditi sve takve uređene parove (i samo njih), jer između [latex]\frac{r\left(r-1\right)}{2}[/latex] i [latex]\frac{r\left(r+1\right)}{2}[/latex] postoji točno [latex]r[/latex] prirodnih brojeva, a znamo da (različitih) uređenih parova [latex]\left(p,\,q\right)[/latex] za koje je [latex]p+q=r+1[/latex] ima točno [latex]r[/latex].
Sada jednostavno za svaki prirodan broj [latex]n[/latex] i njemu pripadajući prirodan [latex]r[/latex], stavimo da je [latex]p:=n-\frac{r\left(r-1\right)}{2}[/latex], te [latex]q:=r-p+1[/latex]. Na taj način smo svakom prirodnom broju [latex]n[/latex] bijektivno pridružili uređeni par prirodnih brojeva [latex]\left(p,\,q\right)[/latex].
Ovime smo pokazali da je skup [latex]\mathbb{N} \times \mathbb{N}[/latex] prebrojiv.
Znamo da je skup [latex]\mathbb{Z}[/latex] prebrojiv, dakle, postoji bijekcija s [latex]\mathbb{N}[/latex] na [latex]\mathbb{Z}[/latex]. Uzmimo tu bijekciju i nazovimu ju [latex]f[/latex].
Sada jednostavno svakom prirodnom broju [latex]n[/latex] na gore opisan bijektivan način pridružimo uređeni par prirodnih brojeva [latex]\left(p,\,q\right)[/latex], zatim tom uređenom paru na bjektivan način pridružimo par [latex]\left(f\left(p\right),\,q\right)[/latex]. Ovime smo očito konstruirali bijekciju s [latex]\mathbb{N}[/latex] na [latex]\mathbb{Z} \times \mathbb{N}[/latex]. A znamo da je skup [latex]\mathbb{Q}[/latex] zapravo identičan skupu [latex]\mathbb{Z} \times \mathbb{N}[/latex].
Q.E.D. :bananawallaby:
Prvo pokažemo da su 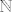 i i 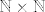 ekvipotentni: ekvipotentni:
Očito je da za svaki  postoji jedinstveni postoji jedinstveni 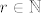 takav da je takav da je
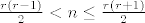 . .
Dalje, želimo konstruirati bijekciju s 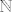 na na 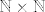 . U skupu . U skupu 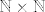 se nalaze uređeni parovi. Neka je uređeni par jednak se nalaze uređeni parovi. Neka je uređeni par jednak 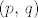 . Lako je za vidjeti da (različitih) uređenih parova za koje je . Lako je za vidjeti da (različitih) uređenih parova za koje je 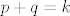 , za neki , za neki 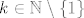 ima točno ima točno 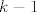 . .
Sada ćemo za svaki 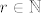 onim prirodnim onim prirodnim  -ovima za koje je -ovima za koje je 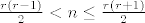 bijektivno pridružiti uređen par bijektivno pridružiti uređen par 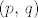 i to takav da je i to takav da je 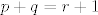 . Na taj ćemo način pogoditi sve takve uređene parove (i samo njih), jer između . Na taj ćemo način pogoditi sve takve uređene parove (i samo njih), jer između 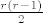 i i 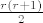 postoji točno postoji točno  prirodnih brojeva, a znamo da (različitih) uređenih parova prirodnih brojeva, a znamo da (različitih) uređenih parova 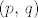 za koje je za koje je 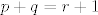 ima točno ima točno  . .
Sada jednostavno za svaki prirodan broj  i njemu pripadajući prirodan i njemu pripadajući prirodan  , stavimo da je , stavimo da je 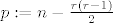 , te , te 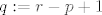 . Na taj način smo svakom prirodnom broju . Na taj način smo svakom prirodnom broju  bijektivno pridružili uređeni par prirodnih brojeva bijektivno pridružili uređeni par prirodnih brojeva 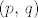 . .
Ovime smo pokazali da je skup 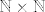 prebrojiv. prebrojiv.
Znamo da je skup 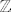 prebrojiv, dakle, postoji bijekcija s prebrojiv, dakle, postoji bijekcija s 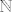 na na 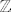 . Uzmimo tu bijekciju i nazovimu ju . Uzmimo tu bijekciju i nazovimu ju  . .
Sada jednostavno svakom prirodnom broju  na gore opisan bijektivan način pridružimo uređeni par prirodnih brojeva na gore opisan bijektivan način pridružimo uređeni par prirodnih brojeva 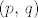 , zatim tom uređenom paru na bjektivan način pridružimo par , zatim tom uređenom paru na bjektivan način pridružimo par 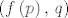 . Ovime smo očito konstruirali bijekciju s . Ovime smo očito konstruirali bijekciju s 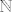 na na 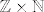 . A znamo da je skup . A znamo da je skup 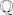 zapravo identičan skupu zapravo identičan skupu 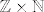 . .
Q.E.D. 
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
 Postano: 18:44 pon, 16. 2. 2009 Naslov: Postano: 18:44 pon, 16. 2. 2009 Naslov: |
    |
|
|
funkcija, surjekcija, injekcija, prost broj, dokaz da prostih ima beskonacno mnogo, kardinalni broj, cantor-b teorem, interpolacijski polinom(ovo je vjerojatno za visu ocjenu), hornerov algoritam, parcijalni razlomak, nulpolinom...
funkcija, surjekcija, injekcija, prost broj, dokaz da prostih ima beskonacno mnogo, kardinalni broj, cantor-b teorem, interpolacijski polinom(ovo je vjerojatno za visu ocjenu), hornerov algoritam, parcijalni razlomak, nulpolinom...
|
|
| [Vrh] |
|
baloncic
Forumaš s poteškoćama u pisanju


Pridružen/a: 11. 10. 2008. (03:46:21)
Postovi: (23)16
Spol: 
Lokacija: Destination unknown
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
baloncic
Forumaš s poteškoćama u pisanju


Pridružen/a: 11. 10. 2008. (03:46:21)
Postovi: (23)16
Spol: 
Lokacija: Destination unknown
|
|
| [Vrh] |
|
maxic
Forumaš(ica)
Pridružen/a: 10. 02. 2009. (20:11:13)
Postovi: (45)16
|
 Postano: 22:50 pon, 16. 2. 2009 Naslov: Postano: 22:50 pon, 16. 2. 2009 Naslov: |
    |
|
|
Evo ja sam danas bio na usmenom kod profesorice Bombardelli. Imao sam 56 bodova iz kolokvija i zadaća i fakat mi je čudo trebalo da dobijem 4, al sam ja 4 dobio.
Profesorica je na usmenom super, pomaže ti, al ne toliko da ti samo kaže šta da pišeš već te natjera da shvatiš šta treba.
Pitala me definiciju polinoma, relacija, svojstva kompozicije funkcije i da dokažem za asocijativnost, pitala me da definiram skup Q preko relacija (prvi zadatak iz kolokvija koji nisam znao ni tada ni danas). Budući da je curu prije mene pitala nulpolinom i rekla joj da dokaže bilo koji smjer, mene je pitala obrat. Onda je profesorica rekla: "Kolega to je vrlo dobar", i svi sretni i zadovoljni.
Evo ja sam danas bio na usmenom kod profesorice Bombardelli. Imao sam 56 bodova iz kolokvija i zadaća i fakat mi je čudo trebalo da dobijem 4, al sam ja 4 dobio.
Profesorica je na usmenom super, pomaže ti, al ne toliko da ti samo kaže šta da pišeš već te natjera da shvatiš šta treba.
Pitala me definiciju polinoma, relacija, svojstva kompozicije funkcije i da dokažem za asocijativnost, pitala me da definiram skup Q preko relacija (prvi zadatak iz kolokvija koji nisam znao ni tada ni danas). Budući da je curu prije mene pitala nulpolinom i rekla joj da dokaže bilo koji smjer, mene je pitala obrat. Onda je profesorica rekla: "Kolega to je vrlo dobar", i svi sretni i zadovoljni.
|
|
| [Vrh] |
|
martina
Forumaš(ica)

Pridružen/a: 17. 09. 2008. (10:37:22)
Postovi: (7)16
Spol: 
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
 Postano: 23:44 pon, 16. 2. 2009 Naslov: Postano: 23:44 pon, 16. 2. 2009 Naslov: |
    |
|
|
[quote="baloncic"]dokaz da prostih ima beskonacno mnogo??
[/quote]
kaj to nije ono...
Pretpostavis da ih je konacno mnogo, tj da su to p1,p2,...,pn. Onda ih sve izmnozis, i tom umnosku dodas 1. I taj broj nije djeljiv s ni jednim od p1...pn, te je to novi prosti broj, sto povlaci da ih je beskonacno mnogo...
| baloncic (napisa): | dokaz da prostih ima beskonacno mnogo??
|
kaj to nije ono...
Pretpostavis da ih je konacno mnogo, tj da su to p1,p2,...,pn. Onda ih sve izmnozis, i tom umnosku dodas 1. I taj broj nije djeljiv s ni jednim od p1...pn, te je to novi prosti broj, sto povlaci da ih je beskonacno mnogo...
|
|
| [Vrh] |
|
baloncic
Forumaš s poteškoćama u pisanju


Pridružen/a: 11. 10. 2008. (03:46:21)
Postovi: (23)16
Spol: 
Lokacija: Destination unknown
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
 Postano: 9:02 uto, 17. 2. 2009 Naslov: Postano: 9:02 uto, 17. 2. 2009 Naslov: |
    |
|
|
[quote="baloncic"]dokaz da prostih ima beskonacno mnogo??[/quote]
Označimo s p1,p2,...,pn proste brojeve u rastućem poretku,tj. p1<p2<p3... Neka je N=p1p2...pn+1 (umnožak p-ova je ovo), za neki nEN. Očito N>p1,p2,p3,...,pn i N nije djeljiv ni sa jednim od brojeva p1,...,pn (ostatak pri djeljenju s nekim pi, i=1,...,n, je 1). Broj N je prost ili složen. Ako je prost,našli smo prosti broj veći od pn. Ako je složen, prema lemi (svaki prirodan broj veći od 1 se može prikazati kao umnožak 1 ili više prostih brojeva) postoji prosti broj p takav da je N djeljiv s p. No, p!=pi, i=1,...,n, tj.p>pn. Dakle,i u ovom smo slučaju našli prosti broj koji je veći od pn. I time smo dokazali da za svaki prosti broj postoji od njega veći prosti broj.
Ali mislim da možeš i onako da pretpostaviš da ih je konačno mnogo..
A zna li itko definiciju interpolacijskog polinoma,i objasnit što je to? To me stajalo prolaza.. :evil:
| baloncic (napisa): | | dokaz da prostih ima beskonacno mnogo?? |
Označimo s p1,p2,...,pn proste brojeve u rastućem poretku,tj. p1<p2<p3... Neka je N=p1p2...pn+1 (umnožak p-ova je ovo), za neki nEN. Očito N>p1,p2,p3,...,pn i N nije djeljiv ni sa jednim od brojeva p1,...,pn (ostatak pri djeljenju s nekim pi, i=1,...,n, je 1). Broj N je prost ili složen. Ako je prost,našli smo prosti broj veći od pn. Ako je složen, prema lemi (svaki prirodan broj veći od 1 se može prikazati kao umnožak 1 ili više prostih brojeva) postoji prosti broj p takav da je N djeljiv s p. No, p!=pi, i=1,...,n, tj.p>pn. Dakle,i u ovom smo slučaju našli prosti broj koji je veći od pn. I time smo dokazali da za svaki prosti broj postoji od njega veći prosti broj.
Ali mislim da možeš i onako da pretpostaviš da ih je konačno mnogo..
A zna li itko definiciju interpolacijskog polinoma,i objasnit što je to? To me stajalo prolaza.. 
_________________
u raju je lijepo,ali u paklu je ekipa
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 10:43 uto, 17. 2. 2009 Naslov: Postano: 10:43 uto, 17. 2. 2009 Naslov: |
    |
|
|
[quote="bad_angel"]A zna li itko definiciju interpolacijskog polinoma,i objasnit što je to? [/quote]
imas neke tocke recimo [latex]\left( x_1,y_1\right) ,\left( x_2,y_2\right) , ... ,\left( x_n,y_n\right)[/latex]
pri cemu je [latex]x_i \neq x_j , \forall i,j\in\{ 1,2, ... ,n\}, i\neq j[/latex]
i sad zelis dobit polinom koji sadrzi sve te tocke
uzmimo da imas tri tocke da shvatis kako se dolazi do trazenog polinoma
neka je [latex]f[/latex] trazeni polinom
sad, ja ga mogu dobit kao zbroj tri polinoma [latex]f_1,f_2[/latex] i [latex]f_3[/latex]pri cemu ce bit
[latex] f_1(x_1)=y_1, f_1(x_2)=0, f_1(x_3)=0, [/latex]
[latex]f_2(x_1)=0, f_2(x_2)=y_2, f_2(x_3)=0, [/latex]
[latex]f_3(x_1)=0, f_3(x_2)=0, f_3(x_3)=y_3[/latex]
ako je dakle [latex]f=f_1+f_2+f_3[/latex] stvarno vrijedi
[latex] f(x_1)=y_1+0+0=y_1[/latex]
[latex] f(x_2)=0+y_2+0=y_2[/latex]
[latex] f(x_3)=0+0+y_3=y_3[/latex]
sad treba nac formulu za [latex]f_1, f_2[/latex] i [latex]f_3[/latex]
[latex]\displaystyle f_1(x)=y_1\cdot \frac{( x-x_2)( x-x_3)}{(x_1-x_2)(x_1-x_3)}[/latex]
[latex]\displaystyle f_2(x)=y_2\cdot \frac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}[/latex]
[latex]\displaystyle f_3(x)=y_3\cdot \frac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)}[/latex]
i sad opcenito kad imas [latex]n[/latex] tocaka
[latex]\displaystyle f(x)=\sum_{i=1}^{n}\left( y_i \prod_{j=1}^{i-1} \frac{x-x_j}{x_i-x_j} \prod_{j=i+1}^{n} \frac{x-x_j}{x_i-x_j} \right)[/latex]
to ti je interpolacijski polinom... Lagrangeov interpolacijski polinom
| bad_angel (napisa): | | A zna li itko definiciju interpolacijskog polinoma,i objasnit što je to? |
imas neke tocke recimo 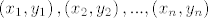
pri cemu je 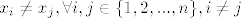
i sad zelis dobit polinom koji sadrzi sve te tocke
uzmimo da imas tri tocke da shvatis kako se dolazi do trazenog polinoma
neka je  trazeni polinom trazeni polinom
sad, ja ga mogu dobit kao zbroj tri polinoma 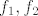 i i 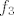 pri cemu ce bit pri cemu ce bit
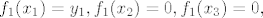
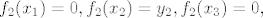
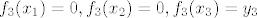
ako je dakle  stvarno vrijedi stvarno vrijedi

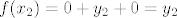
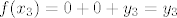
sad treba nac formulu za 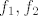 i i 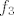
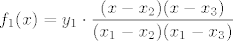
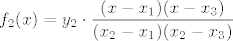
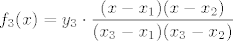
i sad opcenito kad imas  tocaka tocaka
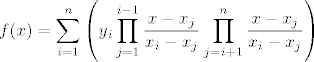
to ti je interpolacijski polinom... Lagrangeov interpolacijski polinom
_________________
Mario Berljafa
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 11:55 uto, 17. 2. 2009 Naslov: Postano: 11:55 uto, 17. 2. 2009 Naslov: |
    |
|
|
[quote="bad_angel"]Zašto to ide tako?
to prema nekoj formuli,ili? :?[/quote]
[latex]\displaystyle f_1(x)=y_1\cdot \frac{( x-x_2)( x-x_3)}{(x_1-x_2)(x_1-x_3)}[/latex]
trebao sam mozda ic malo sporije
trebao sam rec da trazimo polinom, nek sad taj bude [latex]f_{1,1}[/latex] takav da je [latex]f_{1,1}(x_1)=1, f_{1,1}(x_2)=0, f_{1,1}(x_3)=0[/latex]
onda mi je [latex]f_1=y_1\cdot f_{1,1}[/latex]
pa je sad pitanje zasto je [latex]\displaystyle f_{1,1}=\frac{( x-x_2)( x-x_3)}{(x_1-x_2)(x_1-x_3)}[/latex] mozda je malo teze to slozit tako, al, kad jednom vidis i skuzis zasto je tako... ne bi trebalo bit problema, a ako primjetis da kad uvrstis [latex]x_2[/latex], brojnik je [latex]0[/latex], jer je [latex](x_2-x_2)=0[/latex], pa je[latex] f_{1,1}(x_2)=0[/latex], isto kad uvrstis [latex]x_3[/latex], a za [latex]x_1[/latex] imas [latex]\displaystyle f_{1,1}(x_1)=\frac{( x_1-x_2)( x_1-x_3)}{(x_1-x_2)(x_1-x_3)}=1[/latex], e onda skuzis zasto je to tako... i nemas problema :D
| bad_angel (napisa): | Zašto to ide tako?
to prema nekoj formuli,ili?  |
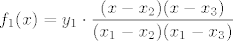
trebao sam mozda ic malo sporije
trebao sam rec da trazimo polinom, nek sad taj bude 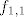 takav da je takav da je 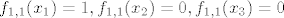
onda mi je 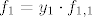
pa je sad pitanje zasto je 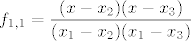 mozda je malo teze to slozit tako, al, kad jednom vidis i skuzis zasto je tako... ne bi trebalo bit problema, a ako primjetis da kad uvrstis mozda je malo teze to slozit tako, al, kad jednom vidis i skuzis zasto je tako... ne bi trebalo bit problema, a ako primjetis da kad uvrstis 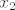 , brojnik je , brojnik je  , jer je , jer je 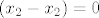 , pa je , pa je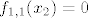 , isto kad uvrstis , isto kad uvrstis 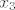 , a za , a za 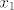 imas imas 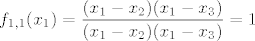 , e onda skuzis zasto je to tako... i nemas problema , e onda skuzis zasto je to tako... i nemas problema 
_________________
Mario Berljafa
|
|
| [Vrh] |
|
baloncic
Forumaš s poteškoćama u pisanju


Pridružen/a: 11. 10. 2008. (03:46:21)
Postovi: (23)16
Spol: 
Lokacija: Destination unknown
|
|
| [Vrh] |
|
Zildyan
Forumaš(ica)

Pridružen/a: 28. 07. 2008. (13:41:39)
Postovi: (20)16
|
|
| [Vrh] |
|
|













