| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
nero
Gost
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 16:32 uto, 31. 3. 2009 Naslov: Postano: 16:32 uto, 31. 3. 2009 Naslov: |
    |
|
|
rjesenja mi bas nisu pri ruci, cini mi se da su mi ispali rang i defekt 2, u prvom, al nisam siguran, u drugom rang 3, defekt 0, u trecem bazu cini funkcional koji vraca sumu koeficijenata polinoma, peti smo mislim svi radili na vjezbama...
4.
kad razmislis sta to znaci [latex]A\neq 0[/latex], i to napises, onda se sjeti da je [latex]A^2=A[/latex] i onda slijedi tvrdnja (jer sta to znaci da je [latex]dimM\geq 1[/latex])
rjesenja mi bas nisu pri ruci, cini mi se da su mi ispali rang i defekt 2, u prvom, al nisam siguran, u drugom rang 3, defekt 0, u trecem bazu cini funkcional koji vraca sumu koeficijenata polinoma, peti smo mislim svi radili na vjezbama...
4.
kad razmislis sta to znaci 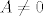 , i to napises, onda se sjeti da je , i to napises, onda se sjeti da je 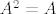 i onda slijedi tvrdnja (jer sta to znaci da je i onda slijedi tvrdnja (jer sta to znaci da je 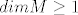 ) )
_________________
Mario Berljafa
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 16:59 uto, 31. 3. 2009 Naslov: Postano: 16:59 uto, 31. 3. 2009 Naslov: |
    |
|
|
zaboravio sam da objasnit taj dio u kojem se dokazuje da je ono potprostor al to je trivijalno...
[quote="Cobs"]uzmes 2 proizvoljna vektora iz M i trebas dokazat da je lin. komb. ta dva vektora isto element od M ---- tu samo iskoristi da je A linearan operator i kako djeluje na vektore iz M[/quote]
ako uzmes [latex]x,y\in \textrm{M}, \alpha ,\beta \in \mathbb{F}[/latex], i gledas sta ce bit sa [latex]\alpha x+\beta y[/latex], ko kaze da operator djeluje na taj vektor?
to isto treba argumentirat...
[quote="Cobs"]da M nije prazan skup[/quote] ne to se ne trazi, npr [latex]0\in \textrm{M}[/latex], pa od tud nis ne zakljucujemo
zaboravio sam da objasnit taj dio u kojem se dokazuje da je ono potprostor al to je trivijalno...
| Cobs (napisa): | | uzmes 2 proizvoljna vektora iz M i trebas dokazat da je lin. komb. ta dva vektora isto element od M ---- tu samo iskoristi da je A linearan operator i kako djeluje na vektore iz M |
ako uzmes 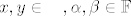 , i gledas sta ce bit sa , i gledas sta ce bit sa  , ko kaze da operator djeluje na taj vektor? , ko kaze da operator djeluje na taj vektor?
to isto treba argumentirat...
| Cobs (napisa): | | da M nije prazan skup |
ne to se ne trazi, npr 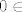 , pa od tud nis ne zakljucujemo , pa od tud nis ne zakljucujemo
_________________
Mario Berljafa
|
|
| [Vrh] |
|
nero
Gost
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 11:43 sri, 1. 4. 2009 Naslov: Postano: 11:43 sri, 1. 4. 2009 Naslov: |
    |
|
|
[quote="Gino"]
ako uzmes [latex]x,y\in \textrm{M}, \alpha ,\beta \in \mathbb{F}[/latex], i gledas sta ce bit sa [latex]\alpha x+\beta y[/latex], ko kaze da operator djeluje na taj vektor?
to isto treba argumentirat...[/quote]
ja mislim da sam sve pojasnio kad sam rekao da treba iskoristiti [b]linearnost [/b]operatora A, no tebi sam jos jednom podebljao.
[quote="Gino"]
ne to se ne trazi, npr [latex]0\in \textrm{M}[/latex], pa od tud nis ne zakljucujemo[/quote]
I mislio sam da ak neki skup ima dim >= 1 da nije prazan, pa ak ti znas neku drugu definiciju, reci mi je
| Gino (napisa): |
ako uzmes 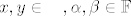 , i gledas sta ce bit sa , i gledas sta ce bit sa  , ko kaze da operator djeluje na taj vektor? , ko kaze da operator djeluje na taj vektor?
to isto treba argumentirat... |
ja mislim da sam sve pojasnio kad sam rekao da treba iskoristiti linearnost operatora A, no tebi sam jos jednom podebljao.
| Gino (napisa): |
ne to se ne trazi, npr 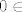 , pa od tud nis ne zakljucujemo , pa od tud nis ne zakljucujemo |
I mislio sam da ak neki skup ima dim >= 1 da nije prazan, pa ak ti znas neku drugu definiciju, reci mi je
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 13:12 sri, 1. 4. 2009 Naslov: Postano: 13:12 sri, 1. 4. 2009 Naslov: |
    |
|
|
[quote="Cobs"]ja mislim da sam sve pojasnio kad sam rekao da treba iskoristiti linearnost operatora A, [b]no tebi sam jos jednom podebljao[/b][/quote] cemu to? pa meni je sve jasno, dal lin operator djeluje na neki vektor ili ne nema veze s njegovom linearnoscu, nego s time dal je taj vektor iz domene
[quote="Cobs"][b]I mislio sam da[/b] ak neki skup ima dim >= 1 da nije prazan, pa ak ti znas neku drugu definiciju, reci mi je[/quote] krivo si mislio, osim sto skupovi nemaju dimenziju, kao sto rekoh nulprostor u sebi sadrzi nulvektor, a dimenzija je 0, dakle skup vektora iz tog prostora nije prazan, a dimenzija je 0
| Cobs (napisa): | | ja mislim da sam sve pojasnio kad sam rekao da treba iskoristiti linearnost operatora A, no tebi sam jos jednom podebljao |
cemu to? pa meni je sve jasno, dal lin operator djeluje na neki vektor ili ne nema veze s njegovom linearnoscu, nego s time dal je taj vektor iz domene
| Cobs (napisa): | | I mislio sam da ak neki skup ima dim >= 1 da nije prazan, pa ak ti znas neku drugu definiciju, reci mi je |
krivo si mislio, osim sto skupovi nemaju dimenziju, kao sto rekoh nulprostor u sebi sadrzi nulvektor, a dimenzija je 0, dakle skup vektora iz tog prostora nije prazan, a dimenzija je 0
_________________
Mario Berljafa
|
|
| [Vrh] |
|
|














