| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
brla
Forumaš(ica)
Pridružen/a: 13. 05. 2009. (22:02:42)
Postovi: (3)16
|
 Postano: 22:09 sri, 13. 5. 2009 Naslov: Trebam pomoć oko riješenja ovog testa |
    |
|
|
Evo u attachu se nalazi test pa bi molio Vas pametne ljude koji to kužite da mi pomognete riješavanjem tog testa. Hvala vam puno...
Evo u attachu se nalazi test pa bi molio Vas pametne ljude koji to kužite da mi pomognete riješavanjem tog testa. Hvala vam puno...
| Description: |
|
| Filesize: |
162.98 KB |
| Viewed: |
170 Time(s) |
|
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja
Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
brla
Forumaš(ica)
Pridružen/a: 13. 05. 2009. (22:02:42)
Postovi: (3)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
| Postano: 22:37 sri, 13. 5. 2009 Naslov: |
|
|
|
[quote="brla"]Evo riješio sam drugi zadatak (riješenje je da jednakost ne vrijedi za sve n brojeve), deseti koji nije problematičan i peti zadatak (riješenje sam dobio x=87 , y=21) valjda je točno.
zanima me prvi zadatak njega ne kužim uopće i ovaj graf funkcije tu sam nešto pokušavao al ne valja.[/quote]
Prvi zadatak se valjda od ova 2 suda treba napraviti neka smislena tvrdnja ,a ta bi bila:
Ako su 2 trokuta sukladna onda su 2 trokuta slična.
(tj sukladnost povlači sličnost)
Tvrdnja vrijedi, obrat ne vrijedi.
U 7.zadatku se samo treba igrat s grafom... prvo se nacrta graf od f(x)=3-2x. To je pravac i to znaš. Onda se od njegga napravi apsolutna vrijednost, tj onaj negativan dio se zrcali preko x-osi. i na kraju se cijeli graf podigne za 2 prema gore da bi se dobilo konačno rješenje.
I zašto 2.zadatak ne bi vrijedio? Meni se čini da vrijedi ;)
| brla (napisa): | Evo riješio sam drugi zadatak (riješenje je da jednakost ne vrijedi za sve n brojeve), deseti koji nije problematičan i peti zadatak (riješenje sam dobio x=87 , y=21) valjda je točno.
zanima me prvi zadatak njega ne kužim uopće i ovaj graf funkcije tu sam nešto pokušavao al ne valja. |
Prvi zadatak se valjda od ova 2 suda treba napraviti neka smislena tvrdnja ,a ta bi bila:
Ako su 2 trokuta sukladna onda su 2 trokuta slična.
(tj sukladnost povlači sličnost)
Tvrdnja vrijedi, obrat ne vrijedi.
U 7.zadatku se samo treba igrat s grafom... prvo se nacrta graf od f(x)=3-2x. To je pravac i to znaš. Onda se od njegga napravi apsolutna vrijednost, tj onaj negativan dio se zrcali preko x-osi. i na kraju se cijeli graf podigne za 2 prema gore da bi se dobilo konačno rješenje.
I zašto 2.zadatak ne bi vrijedio? Meni se čini da vrijedi 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
brla
Forumaš(ica)
Pridružen/a: 13. 05. 2009. (22:02:42)
Postovi: (3)16
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
| Postano: 8:15 čet, 14. 5. 2009 Naslov: |
|
|
|
Istinitost ispitas tablicom istinitosti. 8) Izmedju ostalog, to mozes kod nas naci objasnjeno u [url=http://degiorgi.math.hr/prog1/materijali/p1-vjezbe.pdf]skripti iz Programiranja 1[/url] (PDF, 1021.91kB). :)
Sto se drugog tice, imam dojam da si krivo uvrstio. :) Za koji [i]n[/i] si dobio da stvar ne vrijedi? :-k Meni za [i]n[/i] = 1 (to je baza indukcije) i [i]n[/i] = 2 ispada u redu. 8)
Indukciju izvedes tako da pretpostavis da stvar vrijedi za neki [i]n[/i] i onda racunas za [i]n[/i] + 1:
[latex]\frac{1^2}{1 \cdot 3} + \frac{2^2}{3 \cdot 5} + \dots \frac{n^2}{(2n-1) \cdot (2n+1)} + \frac{(n+1)^2}{(2(n+1)-1) \cdot (2(n+1)+1)} = \frac{1^2}{1 \cdot 3} + \frac{2^2}{3 \cdot 5} + \dots \frac{n^2}{(2n-1) \cdot (2n+1)} + \frac{(n+1)^2}{(2n+1) \cdot (2n+3)} = \textnormal{pretpostavka da vrijedi za $n$} = \\
\frac{n(n+1)}{2(2n+1)} + \frac{(n+1)^2}{(2n+1) \cdot (2n+3)}[/latex]
Sada jos ostaje za srediti stvar; trebas dobiti da je to
[latex]\frac{(n+1)((n+1)+1)}{2(2(n+1)+1)}[/latex]
8)
Istinitost ispitas tablicom istinitosti.  Izmedju ostalog, to mozes kod nas naci objasnjeno u skripti iz Programiranja 1 (PDF, 1021.91kB). 
Sto se drugog tice, imam dojam da si krivo uvrstio. Za koji n si dobio da stvar ne vrijedi?  Meni za n = 1 (to je baza indukcije) i n = 2 ispada u redu.
Indukciju izvedes tako da pretpostavis da stvar vrijedi za neki n i onda racunas za n + 1:
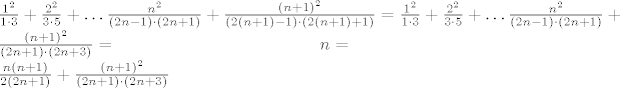
Sada jos ostaje za srediti stvar; trebas dobiti da je to
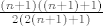
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|
